Переход из одной аффинной системы координат в другую.
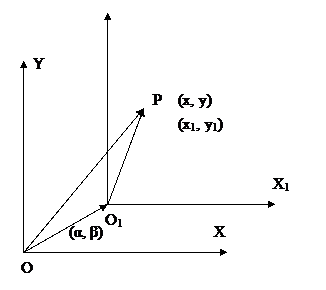 1) Параллельный перенос:
1) Параллельный перенос:
|
Рассмотрим точку Р с в старой системе координат P(x,y), а в новой P(y1, y1).
Рассмотрим вектор ОО1, 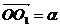 .
.
Координаты точки Р равны координатам радиус вектора O1P в новой системе координат.
Т.к система координат получена параллельным переносом, то координаты старой и новой системы равны и равны (x1, y1).
 2)Переход от одной системы координат к другой, с одним центром:
2)Переход от одной системы координат к другой, с одним центром:
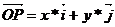
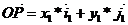
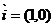
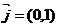
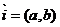
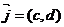
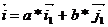
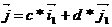
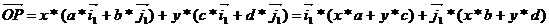
x1=(x*a+y*c) y1=(x*b+y*d)
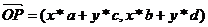
=>P→(x*a+y*c,x*b+y*d)= 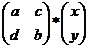
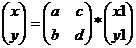 ,
, 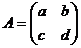
A – матрица перехода от одной системы координат к другой.
Замечание:
- Первый столбец матрицы перехода состоит из координат первого старого базисного вектора в новом базисе.
- Второй столбец матрицы перехода состоит из координат второго старого базисного вектора в новом базисе.
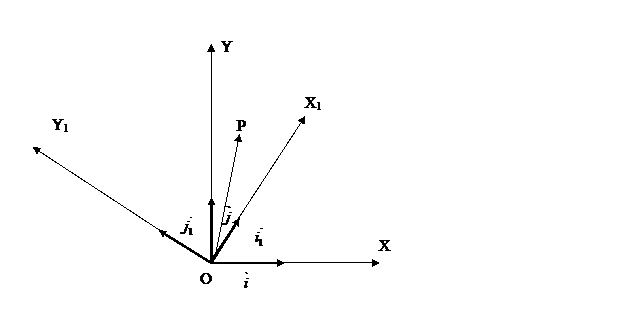
Пусть в плоскости есть XOY – старая система координат и X1O1Y1 – новая система координат.
Общая формула: 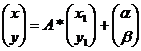
A – матрица 2*2, в первом столбце координаты старого базисного вектора в новом базисе, аналогично для второго столбца.
OO1=(α, β) – в старом базисе.
Следствие: преобразование прямоугольных координат.
Пусть XOY – старая прямоугольная система координат, X1O1Y1 – новая прямоугольная система координат. 
Переход от XOY к X1O1Y1 задаётся углом поворота α.
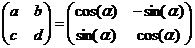
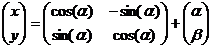
Скалярная и векторная проекция вектора на вектор.
 |
Вектор 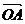 называется векторной проекцией вектора
называется векторной проекцией вектора  на вектор
на вектор  .
.
Скалярной проекцией вектора  на вектор
на вектор  называется число, по модулю равное длине вектора
называется число, по модулю равное длине вектора 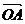 и имеющее знак плюс,
и имеющее знак плюс, 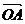 ↑↑
↑↑  и знак минус, если
и знак минус, если 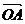 ↑↓
↑↓  .
.
Пр(  ,
,  ) – скалярная проекция .
) – скалярная проекция .
Пр(  ,
,  )=|
)=|  |*cos(γ)=
|*cos(γ)= 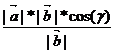
Скалярное произведение векторов.
Пусть  и
и  два данных вектора, чтобы найти угол между ними надо совместить их начала и взять наименьший угол из двух возникающих.
два данных вектора, чтобы найти угол между ними надо совместить их начала и взять наименьший угол из двух возникающих.
Скалярным произведение двух векторов называется  и
и  называется число, которое обозначается (
называется число, которое обозначается (  ,
,  ) и равное |
) и равное |  |*|
|*|  |*cos(α), где α - угол между векторами
|*cos(α), где α - угол между векторами  и
и  .
.
Свойства скалярного произведения векторов:
1) коммутативность ((  ,
,  )=(
)=(  ,
,  ))
))
Доказательство: (  ,
,  )=|
)=|  |*|
|*|  |*cos(α)= |
|*cos(α)= |  |*|
|*|  |*cos(α)=(
|*cos(α)=(  ,
,  )
)
2) линейность по первому аргументу
а) (λ*  ,
,  )=λ*(
)=λ*(  ,
,  )
)
Доказательство: 1) λ=0 слева и справа ноль
2) λ≠0 (λ*  ,
,  )=|λ*
)=|λ*  |*|
|*|  |*cos(α1)= λ*|
|*cos(α1)= λ*|  |*|
|*|  |*cos(α)
|*cos(α)
λ*  //
//  , λ*
, λ*  ↑↑
↑↑  => α1=α => (λ*
=> α1=α => (λ*  ,
,  )=λ*(
)=λ*(  ,
,  )
)
б) 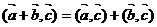
Доказательство: 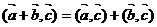
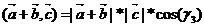
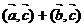 =
= 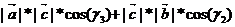
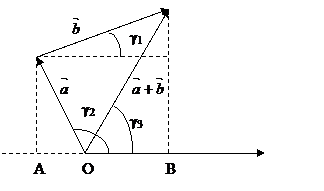
ОА – векторная проекция вектора  на вектор
на вектор 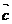 .
.
АВ – векторная проекция вектора  на вектор
на вектор 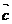 .
.
ОВ – векторная проекция вектора  +
+  на вектор
на вектор 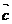
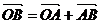
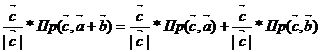
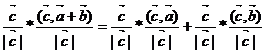
=> 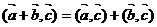 .
.
3) 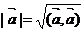
Доказательство:
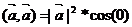
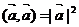
4) Скалярное произведение векторов является критерием ортогональности векторов
 ┴
┴  <=> (
<=> (  ,
,  )=0
)=0
Доказательство:
Нулевой вектор будем считать ортогональным любому вектору
а) Дано: (  ,
,  )=0
)=0
|  |≠0, |
|≠0, |  |≠0, cos(γ)=0 =>
|≠0, cos(γ)=0 =>  ┴
┴ 
б) Дано:  ┴
┴ 
 |≠0, |
|≠0, |  |≠0, cos(γ)=0 => (
|≠0, cos(γ)=0 => (  ,
,  )=0
)=0
Пусть |  |=0 => (
|=0 => (  ,
,  )=0
)=0
5) Выражение скалярного произведения в координатах:
Пусть: 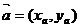 ,
,  =(xb,yb).
=(xb,yb).
Теорема: (  ,
,  )=xa*xb+ya*yb
)=xa*xb+ya*yb
Доказательство:
 =xa*
=xa* 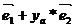
 = xb*
= xb* 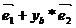
(  ,
,  )=(xa*
)=(xa* 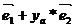 , xb*
, xb* 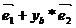 )=
)=
по свойству 2 скалярное произведение является линейным и по 2 аргументу
(  ,λ*
,λ*  )=(λ
)=(λ  ,
,  )=λ*(
)=λ*(  ,
,  )=λ*(
)=λ*(  ,
,  )
)
(  ,
,  +
+ 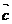 )=(
)=( 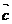 +
+  ,
,  )=(
)=(  ,
,  )+(
)+( 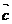 ,
,  ) =(
) =(  ,
,  )+(
)+(  ,
, 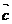 )=
)=
= (xa* 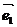 , xb*
, xb* 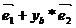 ) + (
) + ( 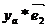 , xb*
, xb* 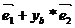 ) = (xa*
) = (xa* 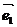 , xb*
, xb* 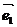 ) + (xa*
) + (xa* 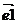 ,
, 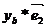 ) + (
) + ( 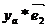 , xb*
, xb* 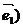 + (
+ ( 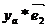 ,
, 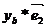 ) = xa*xb*(
) = xa*xb*( 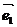 ,
, 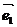 ) + xA*yb (
) + xA*yb ( 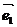 ,
, 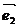 ) + ya*xb*(
) + ya*xb*( 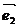 ,
, 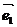 + ya*xb*(
+ ya*xb*( 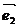 ,
, 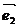 ) = xa*xB*(
) = xa*xB*( 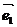 ,
, 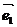 ) + ya*xb*(
) + ya*xb*( 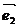 ,
, 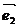 ) = xa*xb + ya*xb
) = xa*xb + ya*xb
