Теорема о коллинеарных векторах.
Векторная алгебра.
Вектора. Операции над ними.
Вектор – направленный отрезок, соединяющий две точки, одна точка называется началом вектора, другая – концом вектора.
Два вектора называются равными если:
1. вектор  и вектор
и вектор  колениарны(
колениарны(  //
//  ).
).
2. длина вектора  равна длине вектора
равна длине вектора  (|
(|  |=|
|=|  |).
|).
3. вектор  и вектор
и вектор  сонаправленны (
сонаправленны ( 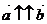 ).
).
Из сформулированного определения вектора следует, что получающиеся один из другого с помощью параллельного переноса называются равными.
Свободным вектором называется класс равных векторов.
Замечание: далее под свободным вектором будет пониматься свободный вектор.
Операции над векторами.
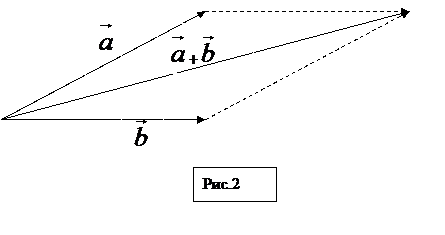
1) I. Сложение векторов – надо параллельно перенести  его так, чтобы его начало совпало с концом вектора
его так, чтобы его начало совпало с концом вектора  . Искомым вектором будет вектор соединяющий начала вектора
. Искомым вектором будет вектор соединяющий начала вектора  и конец вектора
и конец вектора  .
.
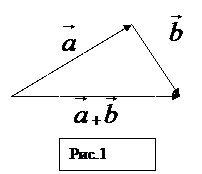
II. вычитание
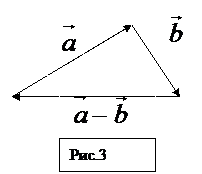 |
III. Сумма n векторов: надо перенести их так, чтобы начало следующего с концом предыдущего, суммой векторов будет вектор соединяющий начало первого вектора и конец последнего вектора.
2) Умножение вектора на число ( 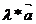 ).
).
Полученный вектор удовлетворяет следующим условиям:
-
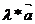 //
// 
- |
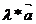 | =
| = 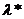 |
|  |
| -
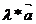
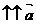 , если λ≥0
, если λ≥0
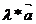
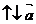 , если λ≤0
, если λ≤0
Аффинная система координат.
Для того, чтобы задать аффинную систему координат надо:
1. выбрать точку О, которая будет началом отсчета.
2. провести две прямые под произвольным углом через точку О.
3. ориентирование прямых(берутся два вектора 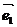 на ОХ и
на ОХ и 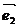 на ОУ(эти вектора берутся произвольной длинны)). Замечание:
на ОУ(эти вектора берутся произвольной длинны)). Замечание: 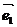 и
и 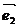 - базисные вектора аффинной системы координат.
- базисные вектора аффинной системы координат.
|
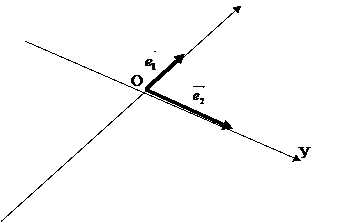
Прямоугольная система координат.
Аффинная система координат называется прямоугольной, если:
1. прямая ОХ перпендикулярна прямой ОУ(ОХ┴ОУ).
2. длинны базисных векторов равны между собой(| 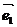 |=|
|=| 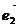 |).
|).
Координаты вектора в аффинной системе координат.
 |
- перенесем вектор
 в точку О.
в точку О. - через конец вектора
 проведем прямую //ОХ, а её точку пересечения с прямой ОУ обозначим через В.
проведем прямую //ОХ, а её точку пересечения с прямой ОУ обозначим через В. - через конец вектора
 проведем прямую //ОУ, а её точку пересечения с прямой ОХ обозначим через А.
проведем прямую //ОУ, а её точку пересечения с прямой ОХ обозначим через А.
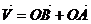
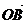 - проекция вектора
- проекция вектора  на ОХ(
на ОХ( 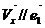 )
)
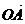 - проекция вектора
- проекция вектора  на ОУ(
на ОУ( 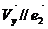 )
)
из этого следует, что 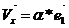 и
и 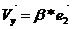
=> 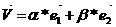 - выражение вектора
- выражение вектора  через базисные вектора
через базисные вектора 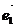 и
и 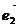 .
.
Координатами вектора  в аффинной системе координат называются соответствующие коофиценты в выражение вектора через базис, т.е. координаты вектора
в аффинной системе координат называются соответствующие коофиценты в выражение вектора через базис, т.е. координаты вектора  =(α, β).
=(α, β).
Координаты точки в аффинной системе координат.
Радиус векторам называется вектор с началом в начале координат(точка О) и концом в точке Р.
 Координаты точки Р – координаты радиус вектора к точке Р.
Координаты точки Р – координаты радиус вектора к точке Р.
Замечание: длину вектора мы будем вычислять только в прямоугольной системе координат.
Пусть в прямоугольной системе координат дан вектор  с координатами (α, β).
с координатами (α, β).
Длинна вектора  : |
: |  |=
|= 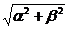 .
.
Линейные комбинации векторов.
Направляющие косинусы.
Пусть в трёхмерном пространстве есть прямоугольная система координат XYZ.
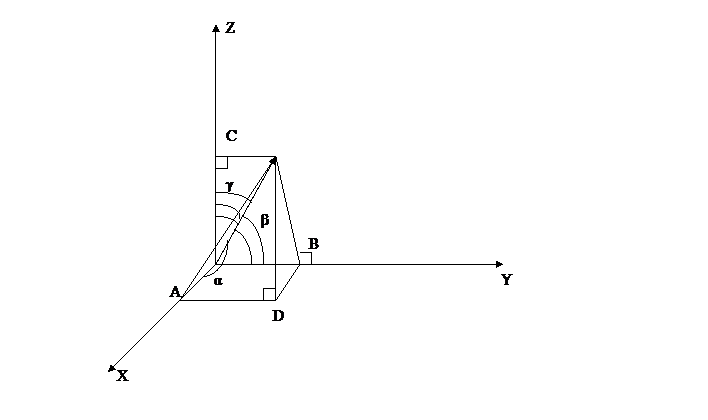
Обозначим через α угол между вектором  и лучом ОХ, через β угол между вектором
и лучом ОХ, через β угол между вектором  и лучом ОY, через γ угол между вектором
и лучом ОY, через γ угол между вектором  и лучом ОZ.
и лучом ОZ.
Определение: cos α, cos β, cos γ – направляющие косинусы вектора  .
.
Теорема: 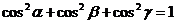 .
.
Доказательство: проведем через конец вектора  :
:
- прямую перпендикулярную ОХ, эта прямая пересекает ОХ в точки А.
- прямую перпендикулярную ОY, эта прямая пересекает ОY в точки B.
- прямую перпендикулярную ОZ, эта прямая пересекает ОХ в точки C.
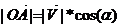
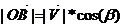
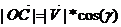
Проведем через конец вектора  прямую перпендикулярную плоскости (XOY), эта прямая пересекает плоскость (XOY) в точке D, через точку D проведем прямую перпендикулярную ОХ и так далее будем проводить прямые перпендикулярные к осям.
прямую перпендикулярную плоскости (XOY), эта прямая пересекает плоскость (XOY) в точке D, через точку D проведем прямую перпендикулярную ОХ и так далее будем проводить прямые перпендикулярные к осям.
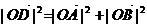 ,
, 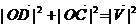 =>
=> 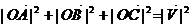
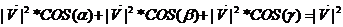 =>
=> 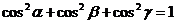 .
.
Полярная система координат
Для того, чтобы в плоскости задать полярную систему координат надо:
- В плоскости выбрать точку О, которая называется полюсом.
- Через точку О провести прямую ОХ и ориентировать её (направить её).
- Нужно выбрать в плоскости положительное направление вращения.
- Выбрать на оси ОХ масштаб.
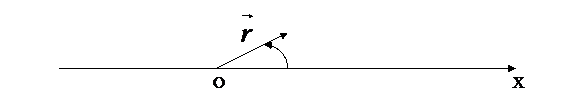 |
- Рассмотрим точку Р.
- Проведем радиус вектор к точке Р.
- Первая полярная координата точки Р – длинна радиус вектора.
- Найдем угол γ =
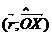 с учетом выбранного направления вращения, угол γ называется второй полярной координатой точки Р.
с учетом выбранного направления вращения, угол γ называется второй полярной координатой точки Р.
Р 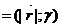
Полярной системе координат можно однозначно сопоставить прямоугольную систему координат. Пусть полюс О будет центром, ось ОХ – осью ОХ прямоугольной системы координат. Проведем прямую перпендикулярную ОХ, это и будет ось OY. Если вращение против часовой стрелки, то ось OY направлена вверх, и наоборот.
Прямоугольной системе координат можно однозначно сопоставить полярную систему координат.
Пусть известна полярные координаты точки Р 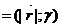 => координат в прямоугольной системе координат координаты точки Р=(r*cos(γ); r*sin(γ)).
=> координат в прямоугольной системе координат координаты точки Р=(r*cos(γ); r*sin(γ)).
Р(X;Y) => 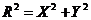 ,
, 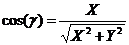
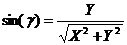
Общее уравнение прямой.
Уравнение вида A*x + B*y + C=0 называется общим уравнением прямой.
Уравнение вида A*x + B*y + C=0 задает прямую в плоскости
Доказательство:
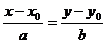 =>b*(x-x0)=a*(y-y0)=>b*x – a*y + (a*y0 - b*x0)=0
=>b*(x-x0)=a*(y-y0)=>b*x – a*y + (a*y0 - b*x0)=0
Заменим b на A, -а на B, (a*y0 - b*x0) на С.
=> A*x + B*y + C=0.
Теорема
Уравнение A*x + B*y + C=0, где 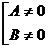 , является уравнением прямой в плоскости с направляющим вектором (-В,А).
, является уравнением прямой в плоскости с направляющим вектором (-В,А).
Доказательство:
Пусть (x0,y0) – решение уравнения, то есть A*x0 + B*y0 + C=0,
вычтем его из исходного уравнения,
получим: A*(x-x0)+B*(y-y0)=0 – полученное уравнение эквивалентно.
A*(x-x0)=-B*(y-y0)=> 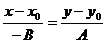 - это уравнение прямой с направляющим вектором (-В,А).
- это уравнение прямой с направляющим вектором (-В,А).
Критерий коллинеарнности вектора прямой.
Вектор 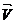 с координатами (a,b) будет коллинеарен прямой L: A*x + B*y + C=0 тогда, и только тогда, когда A*a+B*b=0.
с координатами (a,b) будет коллинеарен прямой L: A*x + B*y + C=0 тогда, и только тогда, когда A*a+B*b=0.
Доказательство:
Пусть точка P0 с координатами (x0,y0) принадлежит прямой L.
(=>)Приложим вектор 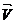 к точке P0. => P1=( x0+a, y0+b)
к точке P0. => P1=( x0+a, y0+b)
=> A*(x0+a) B*(y0+b)+C=0 => A*x0 + A*a + B*y0 + B*b+C=0
A*a + B*b + (A*x0 + B*y0 + C)=0, A*x0 + B*y0 + C=0 т.к. P1 принадлежит L
=> A*a+B*b=0
(<=) не дано надо стрясти.
Все сказанное относится к произвольной аффинной системе координат.
Геометрический смысл коэффициентов.
( 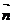 ,
, 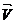 )=A*B – B*A=0
)=A*B – B*A=0
В прямоугольной системе координат (А;В) – координаты вектора нормали.
Уравнения плоскости.
1) Общее уравнение плоскости
Уравнение вида A*x+B*y+C*z+D=0 называется общим уравнением плоскости.
Уравнение A*x+B*y+C*z+D=0 является уравнением плоскости.
Уравнение является A*x+B*y+C*z+D=0 уравнением плоскости.
Доказательство:
Пусть есть плоскость γ. Точка Р0(x0,y0,z0) и вектора  (xa,ya,za),
(xa,ya,za),  (xb,yb,zb) лежат в плоскости γ, Вектора
(xb,yb,zb) лежат в плоскости γ, Вектора  и
и  не коллениарны.
не коллениарны.
Пусть точка Р(x,y,z) не лежит в плоскости γ.
 =( x-x0,y-y0,z-z0)
=( x-x0,y-y0,z-z0)
Точка Р принадлежит плоскости γ тогда и только тогда, когда тройка векторов  ,
,  ,
,  является компланарной, то есть <
является компланарной, то есть < 

 >=0.
>=0.
 =0
=0
(x-x0)*  - (y-y0)*
- (y-y0)*  + (z-z0)*
+ (z-z0)*  =0
=0
Заменим:  = A,
= A,  = -B,
= -B,  =C
=C
Так как вектора не коллениарны, то хотя бы один из трёх определителей не равен нулю.
(x-x0)*A - (y-y0)* B+ (z-z0)* C=0
A*x + B*y + C*z – (A*x0 + B*y0 + C*z0)=0, – (A*x0 + B*y0 + C*z0)=D
A*x + B*y + C*z + D=0
Уравнение A*x + B*y + C*z +D=0 задаёт плоскость(Противоположно предыдущей теореме).
Доказательство:
A*x + B*y + C*z +D=0, A≠0 (1)
Р(x0,y0,z0), пусть Р является решением уравнения (1)
A*x0 + B*y0 + C*z0 + D=0 (2)
(1)-(2): A*(x-x0) – B*(y-y0)+ C*(z-z0)=0 (3)
Уравнение (3) эквивалентно (1)

 , А≠0
, А≠0
 - это уравнение (3).
- это уравнение (3).
Из доказательства предыдущей теоремы следует, что уравнение (3) – уравнение плоскости, содержащей точку Р(x0,y0,z0),  (-B, A, 0),
(-B, A, 0),  (-C, 0, A), вектора
(-C, 0, A), вектора  и
и  не коллениарны => исходное уравнение задаёт плоскость.
не коллениарны => исходное уравнение задаёт плоскость.
Следствие: Пусть плоскость имеет уравнение A*x + B*y + C*z +D=0 => плоскость содержит 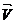 (-B, A, 0) и
(-B, A, 0) и  (-С, 0, А).
(-С, 0, А).
Найдем вектор нормали к плоскости в прямоугольной системе координат.
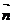 =[
=[ 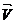 ,
,  ]=(
]=(  , B*A, C*A)=(A, B, C)
, B*A, C*A)=(A, B, C)
Таким образом можно сформулировать геометрический смысл коэффициентов в общем уравнение плоскости: А,В,С – координаты вектора нормали.
2) Параметрическое уравнение плоскости
Уравнение вида  называется параметрическим уравнением плоскости.
называется параметрическим уравнением плоскости.
Уравнение вида  является уравнением плоскости.
является уравнением плоскости.
Доказательство:
Пусть есть плоскость γ. Точка Р0(x0,y0,z0) и вектора  (xa,ya,za),
(xa,ya,za),  (xb,yb,zb) лежат в плоскости γ, Вектора
(xb,yb,zb) лежат в плоскости γ, Вектора  и
и  не коллениарны, также возьмем точку Р(x,y,z).
не коллениарны, также возьмем точку Р(x,y,z).
Точка Р принадлежит плоскости γ тогда и только тогда, когда тройка векторов  ,
,  ,
,  является компланарной, то есть
является компланарной, то есть  =u*
=u*  +v*
+v* 
(x-x0,y-y0,z-z0)=u*(xa,ya,za) + v*(xb,yb,zb)
(x-x0,y-y0,z-z0)=(u*xa, u*ya, u*za) + (v*xb, v*yb, v*zb)


Критерий компланарности вектора плоскости.
Вектор 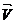 (a, b, c) компланарен γ: A*x+B*y+C*z+D=0 тогда и только тогда, когда A*a+B*b+C*c=0.
(a, b, c) компланарен γ: A*x+B*y+C*z+D=0 тогда и только тогда, когда A*a+B*b+C*c=0.
Доказательство:
Возьмем точку Р0(x0,y0,z0) лежащую в плоскости γ, приложим к этой точке вектор 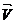 , пусть конец этого вектора в точке Р1=(x1,y1,z1)=(x0+a,y0+b,z0+c).
, пусть конец этого вектора в точке Р1=(x1,y1,z1)=(x0+a,y0+b,z0+c).
Вектор 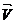 компланарен γ тогда и только тогда, когда точка Р1 принадлежит плоскости γ.
компланарен γ тогда и только тогда, когда точка Р1 принадлежит плоскости γ.
Значит: A*x1+B*y1+C*z1+D=0
A*(x0+a)+B*(y0+b)+C*(z0+c)+D=0
A*a + B*b + C*c + (A*x0 + B*y0 + C*z0) + D=0, A*x0 + B*y0 + C*z0= -D
=> A*a + B*b + C*c =0
Кривые второго порядка.
Эллипс
Пусть в плоскости фиксированы точки F1 и F2, эллипсом называется геометрическое место точек, таких, что сумма расстояний от них до F1 и F2, называемыми фокусами эллипса, есть постоянная величина, обозначаемая через a*2.
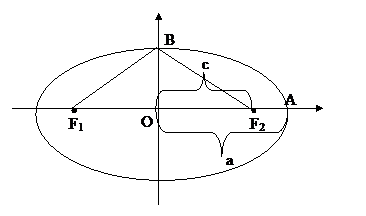
Каноническая система координат эллипса.
· Проведем прямую через фокусы эллипса F1 и F2.(Ox)
· Ориентируем прямую от F1 к F2.
· Середину F1F2 обозначим через О.
· Проведем прямую Oy перпендикулярную Ox.
· Ориентируем прямую так, чтобы система была положительно ориентированна.
Точки пересечения с осями координат – вершины эллипса
Расстояние от фокуса до центра обозначим через с.
АF1 + АF2 =2*а => c + АF2 =а => AF2 =а-c
OA=а – большая полуось эллипса
Рассмотрим треугольник F1F2В – равнобедренный
F1В + F2В=2*а => F1В=F2В=а
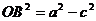 , OB=b – длинна малой полуоси (
, OB=b – длинна малой полуоси ( 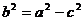 )
)
Эксцентриситетом эллипса называется число 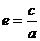 . При е=0 это окружность, а при е=1 это прямая.
. При е=0 это окружность, а при е=1 это прямая.
Директрисами эллипса называется прямые имеющие уравнения 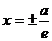
Уравнение эллипса.
Эллипс в канонической системе координат имеет уравнение 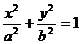 - каноническое уравнение.
- каноническое уравнение.
Доказательство:
1) Докажем, что любая точка эллипса удовлетворяет каноническому уравнению.
Возьмем точку Р(x, y).
d(P,F1)= 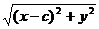 , d(P,F2)=
, d(P,F2)= 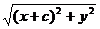
Так как у нас эллипс, то он удовлетворяет условия: d(P,F1)+ d(P,F2)=2*а
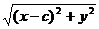 +
+ 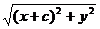 =2*а =>
=2*а => 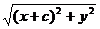 =2*а -
=2*а - 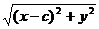
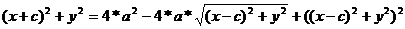
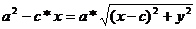
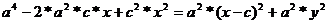
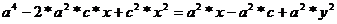
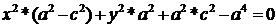
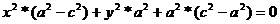 ,
, 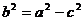
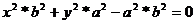
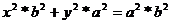
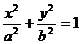
2) (наоборот) Пусть P(x, y) является решением уравнения 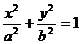 , то есть принадлежит эллипсу.
, то есть принадлежит эллипсу.
d(P,F1)= 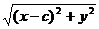 , d(P,F2)=
, d(P,F2)= 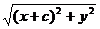
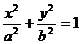 =>
=> 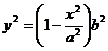
d(P,F2)= 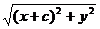 =
= 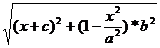 =
= 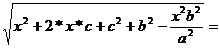
= 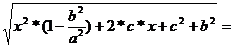
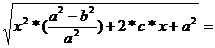
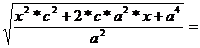
= 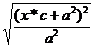 =
= 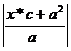 =
= 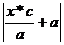 =|e*x+a|
=|e*x+a|
Для d(P,F1) аналогично. d(P,F1)= |e*x-a|
0≤e≤1 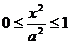
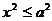 -a≤x≤a
-a≤x≤a
|ex|≤a=> ex+a≥0 => d(P,F2)= ex+a
|ex|≤a=> ex-a≤0 => d(P,F1)= -ex+a=a-ex
d(P,F1)+ d(P,F2)=e*x + a - e*x + a=2*а
Симметрия эллипса
1. Эллипс симметричен относительно оси оХ.
2. Эллипс симметричен относительно оси оY.
3. Эллипс симметричен относительно центра координат.
Пусть эллипс задан каноническим уравнением, точка P(α, β) принадлежит эллипсу. Тогда касательная в точке Р имеет вид: 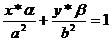
Оптическое свойство эллипса.
Если из одного фокуса эллипса выпустить луч света, то отразившись от эллипса луч попадет в другой фокус.
Гипербола.
Пусть в плоскости даны точки F1 и F2, которые называются фокусами, гиперболой называется геометрическое место точек, таких что модуль разности расстояний от точки до фокусов, есть постоянная величина, обозначаемая через 2*а.

Каноническая система координат гиперболы.
· Проведем прямую через фокусы эллипса F1 и F2.(Ox)
· Ориентируем прямую от F1 к F2.
· Середину F1F2 обозначим через О.
· Проведем прямую оY перпендикулярную Ox.
· Ориентируем прямую так, чтобы система была положительно ориентированна.
F1F2=2*с=> OF1=c
Точки пересечения с осями
OF1=|F1A-F2A|=2*a F1A-F2A=2*a
F1A=c+OA, F2A=c-OA =>2*OA=2*a => OA=a
Расстояние от центра до вершины равно а(как и для эллипса, но a<c)
Введем b: 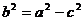
Эксцентриситетом гиперболы называется число e, определенное как 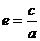 , 1<e<∞
, 1<e<∞
Полученный прямоугольник называется основанием прямоугольной гиперболы.
Прямые, лежащие на диагоналях основного прямоугольника асимптоты гиперболы.
Директрисами гиперболы называются прямые с уравнениями 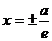 .
.
Каноническое уравнение гиперболы.
Гипербола в канонической для нее системе координат имеет уравнение: 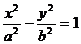
Доказательство:
1)Докажем, что любая точка параболы удовлетворяет каноническому уравнению параболы
Пусть точка P(x,y) принадлежит параболе. F1(-с,0) F2(с,0).
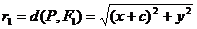
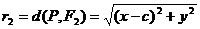
по определению гиперболы: |r1-r2|=2a
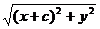 =±2a-
=±2a- 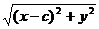
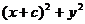 =4a2±2
=4a2±2 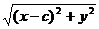 +
+ 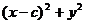
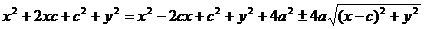
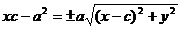
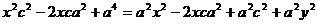
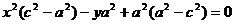 ,
, 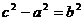 =>
=>
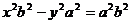
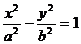
2) Теперь докажем наоборот: пусть P(x, y) является решением уравнения 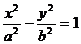 , то есть принадлежит гиперболе.
, то есть принадлежит гиперболе.
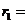 d(P,F1)=
d(P,F1)= 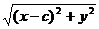 ,
, 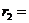 d(P,F2)=
d(P,F2)= 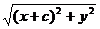
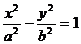 =>
=> 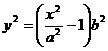
d(P,F2)= 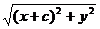 =
= 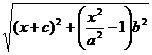 =
= 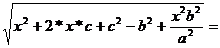
= 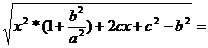
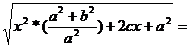
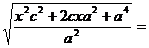
= 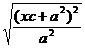 =
= 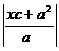 =
= 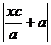 =|ex+a|
=|ex+a|
Для d(P,F1) аналогично. d(P,F1)= |ex-a|
e>1=>
Рассмотрим два случая:
x≤-a
xe-a≤0 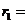 -(xe+a)
-(xe+a)
xe+a≤0 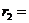 -(ex-a) =>|r1-r2|=2a
-(ex-a) =>|r1-r2|=2a
x≥a
xe-a≥0 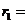 (xe+a)
(xe+a)
xe+a≥0 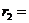 (ex-a) =>|r1-r2|=2a
(ex-a) =>|r1-r2|=2a
=>|r1-r2|=2a => Точка Р принадлежит гиперболе Р.
Симметрия гиперболы.
1. Относительно оси Ох.
2. Относительно оси Oy.
3. Относительно центра системы координат.
Касательная.
Пусть задана парабола 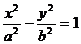 и точка Р(α,β), тогда уравнение касательно в точке Р:
и точка Р(α,β), тогда уравнение касательно в точке Р:
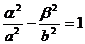
Оптическое свойство гиперболы.
Если из одного из фокусов гиперболы выпустить луч света, то после отражения от гиперболы, луч пойдет по прямой, проходящей через второй фокус.
Парабола.
Пусть дана прямая L, называемая директрисой, и точка F, называемая фокусом, параболой называется геометрическое место точек таких, что расстояние от прямой L до точки F равно расстоянию от точки до фокуса.
Каноническая система параболы.
1. Через точку F проведем прямую перпендикулярную L
2. Ориентируем её от L к F.
3. Отметим точку О – середину отрезка LF.
|

Каноническое уравнение параболы.
В канонической системе координат парабола имеет уравнение 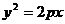 .
.
Доказательство:
1) Вначале докажем, что для любая точка принадлежащая параболе удовлетворяет этому уравнению
Пусть дана точка P(x,y) принадлежащая параболе.
r= 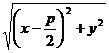 , d=
, d= 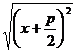 =
= 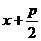 , r=d
, r=d
=> 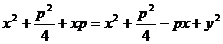
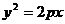
2) Теперь докажем, что, если точка P(x,y) удовлетворяет каноническому уравнению параболу, то она принадлежит параболе.
Дано: r= 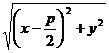 ,
, 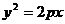 , d=
, d= 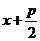
Доказать r=d
r= 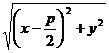 ,
, 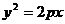 => r=
=> r= 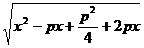 =
= 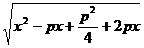 =
= 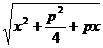 =
=
= 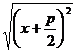 =
= 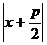 , r≥0 => r=
, r≥0 => r= 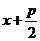
Парабола симметрична относительно оси ОХ.
Эксцентриситет параболы по определению равен еденице.
Оптическое свойство параболы.
Если из фокуса параболы выпустить световые лучи, тогда отразившись от параболы они образуют пучок лучей параллельных оси ОХ.
Векторная алгебра.
Вектора. Операции над ними.
Вектор – направленный отрезок, соединяющий две точки, одна точка называется началом вектора, другая – концом вектора.
Два вектора называются равными если:
1. вектор  и вектор
и вектор  колениарны(
колениарны(  //
//  ).
).
2. длина вектора  равна длине вектора
равна длине вектора  (|
(|  |=|
|=|  |).
|).
3. вектор  и вектор
и вектор  сонаправленны (
сонаправленны ( 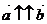 ).
).
Из сформулированного определения вектора следует, что получающиеся один из другого с помощью параллельного переноса называются равными.
Свободным вектором называется класс равных векторов.
Замечание: далее под свободным вектором будет пониматься свободный вектор.
Операции над векторами.
1) I. Сложение векторов – надо параллельно перенести  его так, чтобы его начало совпало с концом вектора
его так, чтобы его начало совпало с концом вектора  . Искомым вектором будет вектор соединяющий начала вектора
. Искомым вектором будет вектор соединяющий начала вектора  и конец вектора
и конец вектора  .
.


II. вычитание
 |
III. Сумма n векторов: надо перенести их так, чтобы начало следующего с концом предыдущего, суммой векторов будет вектор соединяющий начало первого вектора и конец последнего вектора.
2) Умножение вектора на число ( 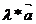 ).
).
Полученный вектор удовлетворяет следующим условиям:
-
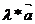 //
// 
- |
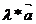 | =
| = 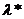 |
|  |
| -
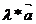
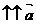 , если λ≥0
, если λ≥0
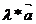
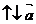 , если λ≤0
, если λ≤0
Аффинная система координат.
Для того, чтобы задать аффинную систему координат надо:
1. выбрать точку О, которая будет началом отсчета.
2. провести две прямые под произвольным углом через точку О.
3. ориентирование прямых(берутся два вектора 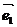 на ОХ и
на ОХ и 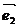 на ОУ(эти вектора берутся произвольной длинны)). Замечание:
на ОУ(эти вектора берутся произвольной длинны)). Замечание: 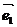 и
и 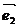 - базисные вектора аффинной системы координат.
- базисные вектора аффинной системы координат.
|
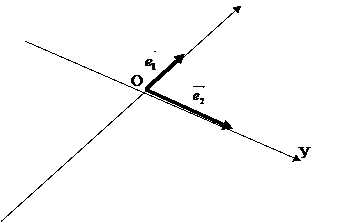
Прямоугольная система координат.
Аффинная система координат называется прямоугольной, если:
1. прямая ОХ перпендикулярна прямой ОУ(ОХ┴ОУ).
2. длинны базисных векторов равны между собой(| 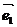 |=|
|=| 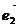 |).
|).
Координаты вектора в аффинной системе координат.
 |
- перенесем вектор
 в точку О.
в точку О. - через конец вектора
 проведем прямую //ОХ, а её точку пересечения с прямой ОУ обозначим через В.
проведем прямую //ОХ, а её точку пересечения с прямой ОУ обозначим через В. - через конец вектора
 проведем прямую //ОУ, а её точку пересечения с прямой ОХ обозначим через А.
проведем прямую //ОУ, а её точку пересечения с прямой ОХ обозначим через А.
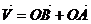
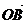 - проекция вектора
- проекция вектора  на ОХ(
на ОХ( 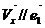 )
)
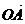 - проекция вектора
- проекция вектора  на ОУ(
на ОУ( 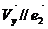 )
)
из этого следует, что 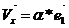 и
и 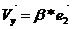
=> 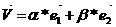 - выражение вектора
- выражение вектора  через базисные вектора
через базисные вектора 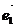 и
и 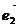 .
.
Координатами вектора  в аффинной системе координат называются соответствующие коофиценты в выражение вектора через базис, т.е. координаты вектора
в аффинной системе координат называются соответствующие коофиценты в выражение вектора через базис, т.е. координаты вектора  =(α, β).
=(α, β).
Координаты точки в аффинной системе координат.
Радиус векторам называется вектор с началом в начале координат(точка О) и концом в точке Р.
 Координаты точки Р – координаты радиус вектора к точке Р.
Координаты точки Р – координаты радиус вектора к точке Р.
Замечание: длину вектора мы будем вычислять только в прямоугольной системе координат.
Пусть в прямоугольной системе координат дан вектор  с координатами (α, β).
с координатами (α, β).
Длинна вектора  : |
: |  |=
|= 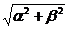 .
.
Теорема о коллинеарных векторах.
два вектора (  и
и  ) коллинеарны (
) коллинеарны (  //
//  ) тогда и только тогда, когда один вектор можно получить из другого посредством умножения на некоторое число α(
) тогда и только тогда, когда один вектор можно получить из другого посредством умножения на некоторое число α(  =α*
=α*  ).
).
<=(достаточность)
 =α*
=α*  =>
=>  // α*
// α*  ,
,  // α*
// α*  =>
=>  //
// 
=>(необходимость)
 ≠0,
≠0,  ≠0
≠0  //
// 
приложим вектора  и
и  к одной точке т.к. вектора параллельны, то они лежат на одной прямой
к одной точке т.к. вектора параллельны, то они лежат на одной прямой
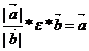
ε=1 если  ↑↑
↑↑ 
ε=-1 если  ↑↓
↑↓ 
=> 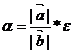 =>
=>  =α*
=α* 
