Общие сведения о системах массового обслуживания
Системой массового обслуживания (СМО) называется любая система, предназначенная для обслуживания каких-либо заявок (требований), поступающих в случайные моменты времени.
Любое устройство, занимающееся обслуживанием заявок, называется каналом обслуживания. СМО бывают:
1) одноканальные (билетная касса с одним кассиром) и многоканальные (касса с несколькими кассирами);
2) с отказами (если все каналы заняты, заявка получает отказ и покидает СМО) и с очередью (если все каналы заняты, заявка становится в очередь и ждет, пока не освободится какой-нибудь канал).
Число мест в очереди m может быть ограниченным или неограниченным. При m = 0 СМО с очередью превращается в СМО с отказом. СМО с очередью различаются по дисциплине обслуживания: обслуживаются ли заявки в порядке поступления, в случайном порядке или некоторые заявки обслуживаются вне очереди.
СМО переходят из состояния в состояние под действием потоков заявок и их обслуживания. Если эти потоки пуассоновские, то СМО называется простейшей. Мы будем рассматривать в дальнейшем только простейшие СМО. Тогда интенсивность потока заявок l равна среднему числу заявок, поступающих в СМО в единицу времени, а интенсивность потока обслуживания m равна среднему числу заявок, обслуживаемых в единицу времени, то есть m = 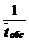 , где
, где 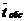 - среднее время обслуживания одной заявки.
- среднее время обслуживания одной заявки.
О работе СМО судят по характеристикам эффективности. Укажем наиболее часто употребляемые из них.
А - абсолютная пропускная способность СМО, то есть среднее число заявок, обслуживаемое СМО в единицу времени.
Q - относительная пропускная способность, то есть вероятность обслуживания поступившей заявки.
Ротк - вероятность отказа, то есть вероятность того, что поступившая заявка не будет обслужена.
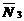 - среднее число заявок, находящихся в СМО (обслуживаемых или ожидающих в очереди).
- среднее число заявок, находящихся в СМО (обслуживаемых или ожидающих в очереди).
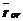 - средняя длина очереди (то есть среднее число заявок в очереди).
- средняя длина очереди (то есть среднее число заявок в очереди).
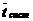 - среднее время пребывания заявки в СМО (в очереди или под обслуживанием).
- среднее время пребывания заявки в СМО (в очереди или под обслуживанием).
 - среднее время пребывания заявки в очереди.
- среднее время пребывания заявки в очереди.
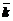 - среднее число занятых каналов.
- среднее число занятых каналов.
В общем случае все эти характеристики зависят от времени, но многие СМО работают в неизменных условиях достаточно долгое время и поэтому в них устанавливается режим, близкий к стационарному. Далее не оговаривая специально, будем приводить вероятности состояний и характеристики эффективности СМО, относящиеся к предельному стационарному режиму ее работы.
СМО называется разомкнутой, если интенсивность поступающего на нее потока заявок не зависит от состояния системы. В этом случае источник заявок находится вне СМО и генерирует неограниченный поток заявок.
Для любой разомкнутой СМО справедливы формулы, связывающие ее различные характеристики эффективности:
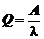 ;
; 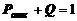 ;
; 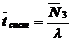 ;
;
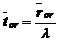 ;
; 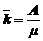 .
.
Эти формулы позволяют искать не все характеристики отдельно, а лишь их часть.
