Задачи, приводящие к модели линейного программирования.

МАТЕМАТИКА

Методические указания

по выполнению контрольных работ

для студентов 2-го курса заочной формы обучения

всех специальностей экономического факультета

Часть 2

Кемерово 2008

Утверждено на заседании кафедры высшей и прикладной математики Кемеровского института (филиала) ГОУ ВПО «РГТЭУ». Протокол № 2 от 22.09.2008 г.

Рекомендовано к печати Учебно-методической комиссией по математическим и информационным дисциплинам Кемеровского института (филиала) ГОУ ВПО «РГТЭУ». Протокол №2 от 22.09.2008 г.

Математика[Текст]: Методические указания по выполнению контрольных работ для студентов 2-го курса заочной формы обучения всех специальностей экономического факультета /Сост.: Л.Н. Гавришина, В.А. Пинаев, Г.И. Шуревич. – Кемерово: Кемеровский институт (филиал) ГОУ ВПО «РГТЭУ», 2008. – 76 с.

В методических указаниях представлены рабочая программа по дисциплине «Математика» для студентов 2-го курса, вопросы для экзамена, две контрольные работы в соответствии с учебным планом и методические указания по их выполнению. Приводится краткий теоретический материал и подробное решение ряда задач.

Составители:

к.ф.-м.н., доцент

Гавришина Л.Н.,

к.ф.-м.н., доцент

Пинаев В.А.,

доцент

Шуревич Г.И.

ТЕМАТИЧЕСКИЙ ПЛАН ДИСЦИПЛИНЫ «МАТЕМАТИКА»

(2-ой год обучения)

3 семестр

1. Линейное программирование.

4 семестр

2. Транспортная задача.

3. Матричные игры.

4. Теория массового обслуживания.

РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ «МАТЕМАТИКА»

(2-ой год обучения)

3 семестр

Раздел 7. Линейное программирование

Задачи линейного программирования. Примеры экономических задач, приводящих к модели линейного программирования. Общая задача линейного программирования (ЗЛП). Основные понятия. Экономико-математическая модель ЗЛП. Графическое решение ЗЛП. Симплекс-метод решения ЗЛП. Преобразование общей модели в каноническую. Признак оптимальности при нахождении максимума и минимума целевой функции. Двойственность в линейном программировании.

4 семестр

Раздел 8. Транспортная задача

Постановка транспортной задачи (ТЗ), ее математическая модель. Нахождение опорного плана методом «северо-западного угла» и методом распределения поставок с учетом наименьших затрат. Метод потенциалов.

Раздел 9. Матричные игры

Матричная игра как модель конфликтной ситуации. Основные понятия матричных игр. Матричная игра двух игроков с нулевой суммой. Матричная игра двух лиц с седловой точкой. Нижняя и верхняя цена игры. Чистые и смешанные стратегии. Игры с природой (принятие решения в условиях риска и неопределенности). Математическое ожидание выигрыша. Критерии Лапласа, Вальда, Севиджа, Гурвица

Раздел 10. Теория массового обслуживания

Управляемый процесс в условиях неопределенности. Случайный процесс. Простейший поток случайных событий в системе массового обслуживания (СМО). Законы распределения вероятностей в простейшем потоке случайных событий в СМО. Математическая модель СМО. Понятие состояния СМО. Предельные вероятности состояний. Размеченный граф состояний СМО. Система дифференциальных уравнений Колмогорова для вероятностей состояний. Основные виды СМО: с отказами, СМО с ограниченной и неограниченной длиной очереди. Характеристики эффективности СМО. Замкнутые СМО, характеристики эффективности.

СПИСОК ЛИТЕРАТУРЫ (основная и дополнительная)

Основная:

1. Акулич И.А. Математическое программирование в примерах и задачах. Высшая школа, 1993.

2. Исследование операций в экономике. Под редакцией профессора Н.Ш. Кремера. М. «Банки и биржи». Издательское объединение «ЮНИТИ», 1997.

3. Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика. Математическое программирование. Минск.:Высшая школа, 1994.

4. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. М.: Высшая школа, 1980.

Дополнительная:

5. Гоголин В.А., Пинаев В.А. Прикладная математика. Кемеровский институт МГУК, 1999 г.

6. Шуревич Г.И. Прикладная математика. Часть 1. Задача линейного программирования. Кемеровский институт МГУК, 1998 г.

7. Шуревич Г.И. Прикладная математика. Часть 2. Транспортная задача. Кемеровский институт МГУК, 1998 г.

8. Шуревич Г.И. Математика. Экономико-математические методы. Ч 1. Линейное программирование, Кемерово, КемИ МГУК, 2001 г.

9. Шуревич Г.И. Математика. Экономико-математические методы. Ч 2. Транспортная задача, Кемерово, КемИ МГУК, 2001 г.

10. Шуревич Г.И. Математика. Экономико-математические методы. Часть 3. Элементы теории матричных игр. Кемерово, КемИ МГУК, 2001 г.

11. Шуревич Г.И. Математика. Экономико-математические методы. Часть 6. Элементы теории массового обслуживания. Кемерово, КемИ МГУК, 2001 г.

КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ ЭКЗАМЕНА ЗА 2 КУРС

ТЕМАТИКА КОНТРОЛЬНЫХ РАБОТ

Темы контрольной работы №3:

1. Графический метод решения задач линейного программирования.

2. Составление экономико-математической модели.

3. Симплекс – метод.

Темы контрольной работы №4:

Транспортная задача.

КОНТРОЛЬНАЯ РАБОТА №3

ВАРИАНТ 0

1. Найти экстремум функции F при следующих ограничениях

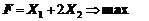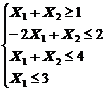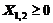2. Составить экономико-математическую модель задачи:

Требуется наилучшим образом вложить «b» долларов в акции трех акционерных предприятий (АП), не более чем по «b_i» долларов в каждое. Цены акций известны: 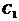, , 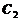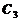. Дивиденды составляют: 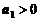, , 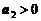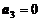. Известно также, что с вероятностью p цена акции третьего АП может вырасти к концу расчетного периода до величины 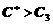. Какой капитал следует вложить в каждое АП, чтобы получить максимальный доход?

3. Решить симплекс - методом.

Магазин оптовой торговли реализует три вида продукции I, II, III. Для этого используются два ограниченных ресурса: полезная площадь помещений, которая составляет 450 м² и рабочее время работников магазина - 600 чел. час. Товарооборот должен быть не менее 240 тыс. руб. Разработать такой план товарооборота, который дает максимум прибыли. Затраты ресурсов на реализацию и получаемая при этом прибыль представлены в таблице.

Продукция Ресурсы	Затраты ресурсов на реализацию	Объем ресурсов
I	II	III
Полезная площадь, м2	1,5
Рабочее время, чел. час.			1,5
Прибыль

ВАРИАНТ 1

1. Найти экстремум функции F при следующих ограничениях

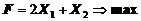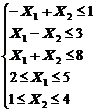2. Составить экономико-математическую модель задачи:

Под посев n культур отведено m земельных участков площадью 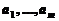га. Средняя урожайность j-ой культуры на i-ом участке составляет 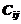центнеров с га. Выручка за один центнер j-ой культуры 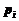рублей. Какую площадь на каждом участке следует отнести под каждую культуру, чтобы получить максимальную выручку, если по плану должно быть собрано не менее 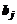центнеров j-ой культуры?

3. Решить симплекс - методом.

Исходя из специализации и своих технологических возможностей фирма может выпускать четыре вида продукции. Сбыт любого количества обеспечен. Для изготовления этой продукции используются трудовые ресурсы, полуфабрикаты и станочное оборудование. Общий объем ресурсов (в расчете на трудовую неделю), расход каждого ресурса на единицу выпускаемой продукции и прибыль, полученная за единицу продукции, приведены в таблице. Требуется определить план выпуска, доставляющий предприятию максимум прибыли.

Продукция Ресурсы	I	II	III	IV	Объем ресурсов
Трудовые ресурсы, чел. час.
Полуфабрикаты, кг.
Станочное оборуд., станк-ч
Цена 1ед. продукции, руб.

ВАРИАНТ 2

1. Найти экстремум функции F при следующих ограничениях

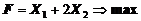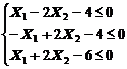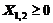2. Составить экономико-математическую модель задачи:

Фирма «Лакомка» выпускает 4 вида полуфабрикатов: А, В, С, Д. Каждый полуфабрикат состоит из ряда ингредиентов (крахмал, сахар, витамины, ...). Всего их n. Пусть индекс i указывает на порядковый номер ингредиента 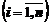, а индекс j указывает на порядковый номер полуфабриката 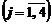. Обозначим через 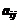количество i-го ингредиента в 1 единице j-го полуфабриката. Предположим, что максимальное количество ингредиента i которым данная фирма располагает, равно 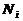. Доход, получаемый с одной единицы j-го полуфабриката, обозначим через 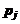. Фирма должна произвести не менее 10000 единиц полуфабриката А, 12500 ед. полуфабриката В, 15000 ед. полуфабриката С и 17000 ед. полуфабриката Д. Требуется построить оптимальный план выпуска продукции А, В, С, Д.

3. Решить симплекс - методом.

Фирма «Лесная пилорама» столкнулась с проблемой наиболее рационального использования ресурсов лесоматериалов, имеющихся в одном из принадлежащих этой фирме лесных массивов. В районе данного массива имеется лесопильный завод и фабрика на которой изготовляется фанера. Таким образом лесоматериалы можно использовать как для производства пиломатериалов, так и для изготовления фанеры. Чтобы получить 2,5 м³ коммерчески реализуемых пиломатериалов, необходимо израсходовать 2,5 м³ еловых и 7,5 м³ пихтовых лесоматериалов. Для приготовления 100 м² фанеры требуется 5 м³ еловых и 10 м³ пихтовых лесоматериалов. Лесной массив содержит 80 м³ и 180 м³ пихтовых лесоматериалов. Согласно условиям поставок, в течение планируемого периода необходимо произвести по крайней мере 10 м³ пиломатериалов и 1200 м² фанеры. Доход с 1 м³ пиломатериалов составляет 16 долларов, а со 100 м² фанеры 60 долларов.

ВАРИАНТ 3

1. Найти экстремум функции F при следующих ограничениях

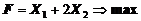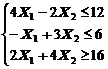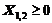2. Составить экономико-математическую модель задачи:

Фирма «Супертранзистор» выпускает радиоприемники трех моделей: А, В, С. Доход за реализацию одной модели вида А составляет 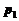рублей, одной модели вида В составляет 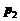рублей, одной модели вида С составляет 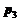рублей. Необходимо, чтобы фирма выпускала за неделю не менее 100 приемников модели А, 150 приемников модели В и 75 приемников модели С. Каждая модель характеризуется определенным временем, необходимым для изготовления соответствующих деталей, сборки изделия, его упаковки: на 10 приемников модели А требуется 3 часа для изготовления деталей, 4 ч на сборку и 1 ч на упаковку; на 10 приемников модели В требуется 3,5 часа для изготовления деталей, 5 ч на сборку и 1,5 ч на упаковку; на 10 приемников модели С требуется 5 часа для изготовления деталей, 8 ч на сборку и 3 ч на упаковку. В течение недели фирма может израсходовать на производство радиодеталей 150 часов, на сборку 200 ч и на упаковку 60 ч. Для решения задачи производственного планирования требуется построить соответствующую модель.

3. Решить симплекс - методом.

Можно закупить корм двух видов (I и II). В каждой единице корма I-го вида содержится 1 ед. витамина А, 2 ед. витамина В и нет витамина С; в каждой единице корма II-го вида - 2 ед. витамина А, 1 ед. витамина В и 1 ед. витамина С. Животному необходимо дать в сутки не менее 10 ед. витамина А, 10 ед. витамина В и 4 ед. витамина С. Составить наиболее дешевый рацион питания животного, если стоимость единицы I-го вида равна 2 денежных единиц, а стоимость единицы корма II-го вида - 4 денежных единиц.

ВАРИАНТ 4

1. Найти экстремум функции F при следующих ограничениях

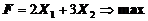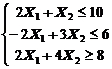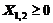2. Составить экономико-математическую модель задачи:

Торговое предприятие реализует n групп товаров. Известны нормативные затраты ресурсов в расчете на единицу каждой j-ой товарной группы а_ij и их общий объем b_i. Целью решения данной задачи является определение оптимальной структуры товарооборота по критерию максимума прибыли F. Исходные данные представлены таблицей:

№	Показатели	Товарная группа	Ограничения по объему
А	В	С
	Рабочее время (чел. час)	0,1	0,2	0,4
	Площадь торговых залов и складов (м2)	0,05	0,02	0,02
	Издержки обращения (руб.)
	Торговая прибыль на ед. товара (руб.)

3. Решить симплекс - методом.

Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в таблице:

Ресурсы	Нормы затрат ресурсов на 1 изд.	Общее кол-во ресурсов
Стол	Шкаф
Древесина I вида	0,2	0,1
Древесина II вида	0,1	0,3
Трудоемкость (челов. час.)	1,2	1,5
Прибыль

Определить, сколько столов и шкафов фабрике следует изготовлять, чтобы прибыль от реализации была максимальной.

ВАРИАНТ 5

1. Найти экстремум функции F при следующих ограничениях

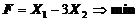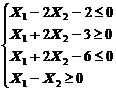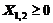2. Составить экономико-математическую модель задачи:

Для изготовления трех видов рубашек используется два вида пуговиц, два вида ниток и один вид ткани. Запасы пуговиц, ниток, ткани, суммарный ресурс рабочего времени, которые можно задействовать при производстве рубашек, а также нормы расхода пуговиц, ниток, тканей и рабочего времени на пошив одной рубашки каждого вида приведены в таблице. Здесь же приведены величины прибыли от реализации одной рубашки каждого вида.

Наименование ресурса	Ед. изм	Объем ресурса	Нормы затрат ресурса на 1 рубашку
рубашка 1в	рубашка 2в	рубашка 3в
Пуговицы 1	шт.
Пуговицы 2	шт
Нитки 1	м
Нитки 2	м
Ткань	м2		1,1	1,4	1,2
Рабочее время	час		0,25	0,3	0,4
Торговая прибыль на ед. товара (р)

Кроме того, ситуация на рынке диктует необходимость выпуска рубашек первого вида не менее 110 штук. Необходимо составить такую программу выпуска продукции, чтобы при заданных ограничениях получить максимальную прибыль.

3. Решить симплекс - методом.

На мебельной фабрике из стандартных листов фанеры необходимо вырезать заготовки трех видов в количествах, соответственно равных 24, 31, 18 шт. Каждый лист фанеры может быть разрезан двумя способами. Количество получаемых заготовок при данном способе раскроя приведено в таблице. В ней же указана величина отходов, которая получается при данном способе раскроя одного листа фанеры.

Вид заготовки	Количество заготовок (шт.) при раскрое по способу
А	В
I
II
III
Величина отходов

Определить, сколько листов фанеры и по какому способу следует раскроить так, чтобы было получено не меньше нужного количества заготовок при минимальных отходах.

ВАРИАНТ 6

1. Найти экстремум функции F при следующих ограничениях

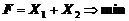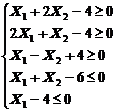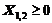2. Составить экономико-математическую модель задачи:

На швейной фабрике ткань может быть раскроена n способами для изготовления нужных швейных изделий. Пусть из А(м²) ткани при 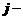ом варианте раскроя 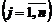изготовляется 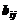деталей 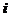-го вида 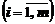, а величина отходов при данном варианте раскроя составляет 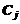м². Известно, что деталей 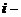го вида следует изготовлять по 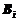штук. Требуется раскроить ткань так, чтобы было получено необходимое количество деталей каждого вида при минимальных общих отходах. Составить математическую модель задачи.

3. Решить симплекс - методом.

На звероферме могут выращиваться черно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используется три вида кормов. Количество корма каждого вида, которое ежедневно должны получать лисицы и песцы, приведено в таблице. В ней же указано общее количество корма каждого вида, которое может быть использовано зверофермой, и прибыль от реализации одной шкурки лисицы и песца.

Вид корма	Кол-во ед. корма которое должны получать	Общее кол-во корма
лисица	песец
I
II
III
Прибыль от реализации 1-ой шкурки

Определить, сколько лисиц и песцов следует выращивать на звероферме, чтобы прибыль от реализации их шкурок была максимальной.

ВАРИАНТ 7

1. Найти экстремум функции F при следующих ограничениях

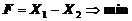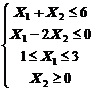2. Составить экономико-математическую модель задачи:

При откорме животных каждое животное должно получить не менее а ед. питательного вещества А, не менее b ед. вещества B, не менее с ед. вещества С. Указанные питательные вещества содержат три вида корма: I, II, III. Содержание единиц питательных веществ в 1 ед. каждого из видов корма приведено в таблице:

Корм Вещества	Количество питательных веществ в 1 ед. корма
I	II	III
А
В
С

Составить дневной рацион, обеспечивающий необходимое количество питательных веществ при минимальных затратах, если цена 1ед. корма I вида составляет Р₁ усл. ден. ед., корма вида II - Р₂ усл. ден. ед. и вида III- Р₃ усл. ден. ед.

3. Решить симплекс - методом.

Фирма выпускает столы двух типов А и В. На производство одного стола вида А требуется 3 м² доски и 12 мин. На производство одного стола вида В требуется 4 м² досок и 30 мин. Прибыль от реализации стола вида А составляет 2 доллара, стола вида В - 4 доллара. За неделю фирма может закупить 1700 м² досок и затратить 160 час. времени. При каком плане выпуска столов прибыль будет максимальной?

ВАРИАНТ 8

1. Найти экстремум функции F при следующих ограничениях

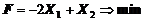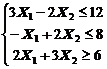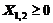2. Составить экономико-математическую модель задачи:

На мебельной фабрике из стандартных листов фанеры необходимо вырезать заготовки трех видов в количествах, соответственно равных N₁, N₂, N₃. Каждый лист фанеры может быть разрезан на заготовки двумя способами А и В. Количество получаемых заготовок при данном способе раскроя приведен в таблице. В ней же указана величина отходов, которая получается при данном способе раскроя одного листа фанеры.

Способы раскроя Вид заготовки	Количество заготовок при раскрое по способу
А	В
I
II
III
Величина отходов

Определить, сколько листов фанеры и по какому способу следует раскроить так, чтобы было получено не менее нужного количества заготовок при минимальных отходах.

3. Решить симплекс - методом.

Имеются три вида сырья А, В, С, которые используются для производства двух видов продуктов - I, II. В распоряжении фирмы-изготовителя находятся 500 ед. сырья А, 750 ед. сырья В и 200 ед. сырья С. Продукт I состоит из 1 ед. сырья А и 2 ед. сырья В. Продукт II состоит из 2 ед. сырья А, 1 ед. сырья В и 1 ед. сырья С. Доход от производства 1 ед. продукта I составляет 4 доллара, а от 1 ед. продукта II - 5 долларов. Сколько единиц каждого продукта следует производить, чтобы максимизировать прибыль?

ВАРИАНТ 9

1. Найти экстремум функции F при следующих ограничениях

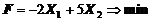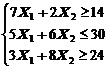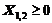2. Составить экономико-математическую модель задачи:

Магазин оптовой торговли реализует три вида продукции П₁, П₂, П₃ при двух ограниченных ресурсах - полезная площадь помещений, которая составляет N м² и рабочее время работников магазина - M чел. час. Товарооборот должен быть не менее Р тыс. руб. Разработать план товарооборота, приносящий максимум прибыли. Затраты ресурсов на реализацию и получаемая при этом прибыль представлены таблицей:

Ресурс	Затраты ресурсов на реализацию, тыс. руб.
П1	П2	П3	Объем ресурса
Полезная площадь м2				N
Рабочее время, чел. час.			2,5	М
Прибыль	С1	С2	С3

Составить математическую модель задачи.

3. Решить симплекс - методом.

Из листового проката определенной формы необходимо вырезать некоторое количество заготовок двух типов А и В для производства 90 штук изделий. Для одного изделия требуется 2 заготовки типа А и 10 заготовок типа В. Возможны четыре варианта раскроя одного листа проката. Количества заготовок А и В, вырезаемых из одного листа при каждом варианте раскроя и отходы от раскроя указаны в таблице.

Вариант раскроя	Заготовки	Отходы от раскроя
А	В
	4 шт.	0 шт.	12 ед.
	3 шт.	3 шт.	5 ед.
	1 шт.	9 шт.	3 ед.
	0 шт.	12 шт.	0 ед.

Какое количество листов проката нужно раскроить каждым вариантом для изготовления 90 штук изделий, чтобы отходы от раскроя были наименьшими?

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Основные понятия линейного программирования

В мире уже накоплен достаточный опыт постановки и решения экономических задач с помощью математических методов.

Прикладная математика имеет очень важное методологическое значение в системе подготовки современного экономиста. В ней четко реализуется одна из основных идей изучения курса высшей математики в экономическом вузе – идея математического моделирования экономических процессов.

В разделах прикладной математики рассматриваются задачи об использовании ресурсов, о смесях, о раскрое материалов, транспортная задача, матричные игры, система планирования и управления, теория массового обслуживания.

В них требуется найти решение, когда некоторый критерий эффективности(например, прибыль, выручка, затраты ресурсов и т.п.) принимает максимальное или минимальное значение.

Задачи теории систем массового обслуживания предназначены для изучения и анализа систем обслуживания с очередями заявок или требований. Их цель – определить показатели эффективности работы системы.

Приведем некоторые определения.

Математическое программирование - это прикладная отрасль математики, которая является теоретической основой решения задач оптимального планирования.

Линейное программирование - это наука о методах исследования и отыскания наименьших или наибольших значений линейной функции, на неизвестные которой наложены линейные ограничения.

Таким образом, задачи линейного программирования относятся к задачам на условный экстремум.

Решение экстремальных экономических задач можно разбить на три этапа:

- построение экономико - математической модели;

- нахождение оптимального решения одним из математических методов;

- практическое внедрение в народное хозяйство.

Экономико-математическая модель - это выражение экономической задачи в виде функций, уравнений, неравенств.

Математическая модель задачи линейного программирования (ЗЛП) содержит:

1) совокупность неизвестных величин, которые должны быть неотрицательны

.

2) целевую функцию, .

3) условия (систему ограничений), налагаемые на неизвестные величины, выраженные в виде уравнений или неравенств.

(1)

Оптимальным решением (или оптимальным планом) называется такое решение системы ограничений, при котором целевая функция принимает оптимальное (max или min) значение.

Систему ограничений (1) заданную в виде неравенств можно привести к системе уравнений, для чего нужно к левой части неравенства прибавить или отнять добавочную переменную.

Таким образом, ЗЛП приводится к канонической форме, когда система ограничений задана в виде системы m линейных уравнений с n переменными.

При этом возможны три случая:

1. Система ограничений несовместна.

Следовательно, ЗЛП не имеет решения.

2. Система ограничений совместная и определенная .

В этом случае система имеет единственное решение .

При этом если: а) хотя бы одна из переменных отрицательна, то полученное решение не может быть допустимым и ЗЛП не имеет решения; б) все переменные - неотрицательные, то найденное решение является допустимым, причем и оптимальным (так как оно единственное).

3. Система ограничений совместная и неопределенная .

У такой системы существует бесчисленное множество решений. Необходимо установить, имеются ли среди них допустимые.

Основные определения.

Любые переменных системы линейных уравнений с переменными называются основными (или базисными), если определитель из коэффициентов при них отличен от нуля. Этот определитель будем называть базисным минором матрицы А, из коэффициентов при переменных.

Тогда остальные переменных называются неосновными или свободными.

Основными могут быть различные группы переменных из , но их количество не превышает числа сочетаний из по :

Из бесчисленного множества решений выделяют базисные решения.

Базисным решением системы линейных уравнений с переменными называется всякое ее решение, в котором неосновные переменные равны нулю.

Каждой группе основных переменных соответствует одно базисное решение.

Базисные решения могут быть допустимыми или недопустимыми.

Базисное решение называется допустимым, если значения основных переменных неотрицательны, а неосновные переменные равны нулю.

Базисное решение называется недопустимым, если хотя бы одно значение переменной отрицательно.

Если в базисном решении хотя бы одна из основных переменных принимает нулевое значение, то оно называется вырожденным.

Симплексный метод

Симплексный метод является универсальным методом, которым можно решить любую задачу линейного программирования.

Идея симплекс – метода

1. Систему ограничений приводят к каноническому виду, то есть к системе m линейных уравнений с n неизвестными.

2. Находят любое ее базисное решение, по возможности наиболее простое.

3. Если первое базисное решение недопустимо, то с помощью симплекс - метода осуществляется переход к другим базисным решениям, пока не будет найдено допустимое базисное решение.

4. Если базисное решение допустимое, то проверяют его на оптимальность.

5. Если оно не оптимально, то переходят к другому допустимому базисному решению.

Симплекс - метод гарантирует на каждом шаге приближение целевой функции к оптимуму.

Таким образом, применение симплекс - метода состоит из двух этапов:

1. Нахождение допустимого базисного решения системы ограничений.

2. Нахождение оптимального решения.

Каждый этап может включать несколько шагов (итераций), соответствующих тому или иному базисному решению. Число этих шагов конечно, так как конечно число базисных решений.

Для перехода к новому базисному решению необходимо решить два вопроса:

1. Установить, какая неосновная переменная должна быть переведена в число основных.

2. Выбрать переменную, которую из основных следует перевести в неосновные на место выбывшей в основные переменные.

Ответ на первый вопрос.

Если базисное решение допустимое, а целевая функция есть функция на нахождение максимума, то берут переменную с наибольшим положительным коэффициентом и переводят ее в основные. Если целевая функция есть функция на нахождение минимума, то берут переменную с наибольшим по абсолютной величине отрицательным коэффициентом и переводят ее в основные.

Если базисное решение недопустимое, то в основные следует переводить те неосновные, которые в уравнении последней системы с отрицательным свободным членом имеют положительные коэффициенты. При этом могут представиться три случая:

1. В i-м уравнении системы уравнений нет неосновных переменных с положительными коэффициентами, то есть все коэффициенты при переменных отрицательные, как и свободный член.

В этом случае данная система ограничений - несовместна, так как она не имеет ни одного допустимого решения.

Если же нет ни одного допустимого решения системы ограничений, то нет и оптимального.

2. В i-м уравнении имеется одна переменная, коэффициент которой положителен. В этом случае в основные переводится именно эта переменная.

3. В i-м уравнении имеется несколько переменных с положительными коэффициентами. В этом случае следует определить минимальное значение для каждой из этих переменных и выбрать ту, минимальное значение которой меньше, чем у других.

Чтобы определить минимальное значение какой-либо переменной, вычисляют абсолютную величину отношения свободного члена уравнения к коэффициенту при этой переменной в этом уравнении.

Например:

Здесь для х₁- это будет: для х₂- это отношение будет равно ¥, так как при любом возрастании х₂ переменная х₃ не может стать отрицательной; для х₄- это будет для х₅- это будет (то есть если переменная отсутствует в уравнении, то для нее отношение считают равным ¥).

Таким образом, если в некоторых уравнениях знаки свободного члена и коэффициента при переменной совпадают или в каких-т