Понятие вероятности и частоты

Вероятность служит мерой объективной возможности появления события.

Вероятность события А обозначается символом Р(А).

Вероятность события А равна отношению числа исходов, благоприятствующих наступлению данного события – 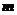, к общему числу всех исходов – 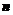, равновозможных, несовместимых и образующих полную группу.

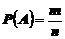(3)

Это определение вероятности называют классическим.

Следует иметь ввиду, что вероятность случайного события изменяется от 0 до 1, 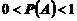. Вероятность достоверного события равна 1; вероятность невозможного события равна 0.

Вероятность противоположного события находится по формуле

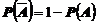(4)

Вероятность события A не следует путать с частотой (частостью) события A.

Частота события А находится как отношение числа опытов, в которых это событие произошло, к общему числу фактически произведенных опытов.

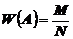(5)

Заметим, что вероятность можно вычислить до опыта, а частоту только после опыта.

Пример 6.Монета подброшена 7 раз. При этом «орел» выпал 2 раза. Тогда вероятность выпадения «орла» равна 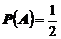, так как всего два исхода опыта (две стороны монеты), а число благоприятствующих исходов равна 1.

Частота выпадения «орла» равна .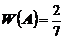

Пример 7.В лотерее играет 1000 билетов. На пять билетов падает выигрыш 200 рублей, на десять билетов – 50 рублей, на 100 билетов – 1 рубль. Остальные билеты не выигрышные. Какова вероятность выиграть по билету а) не менее 50 рублей, б) двести рублей?

Решение. Обозначим события

А – выиграть не менее 50 рублей, В – выиграть 200 рублей.

Тогда ,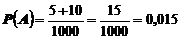

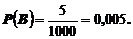
Формулы комбинаторики

При вычислении вероятности по формуле (3) для нахождения 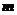и 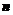применяется та или иная формула комбинаторики, в зависимости от того, каким образом осуществляется выборка элементов из общего их числа.

Если даны 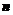различных элементов, то их можно объединить в группы с помощью перестановок 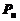, размещений 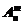и сочетаний .

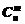С помощью перестановок находится число комбинаций из одних и тех же 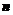различных элементов, которые отличаются только порядком их расположения.

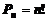(6)

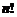–(факториал), , .

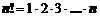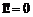Пример 8.Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в число один раз.

Решение. .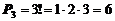

Если опыт состоит в выборе 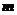элементов из 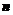элементов без возвращения, но с упорядочиванием их по мере выбора, то число комбинаций находится с помощью размещений.

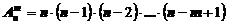(7)

Здесь всего – сомножителей.

Пример 9.Сколько трехзначных чисел можно составить из цифр 1, 2, 3, …9.

Решение. Так как здесь выборка цифр осуществляется без возвращения и важен порядок цифр в числе, то искомое количество чисел находится по формуле (7).

.

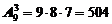В том случае, когда опыт состоит в выборе 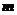элементов из 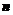элементов без возвращения и без упорядочивания, то число комбинаций находится с помощью сочетаний.

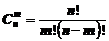. (8)

Пример 10. Из партии товара, в которой 31 изделие стандартных, а 6 изделий бракованных, берут наудачу 3 изделия. Чему равна вероятность, что

а) все три изделия стандартные (А),

б) хотя бы одно изделие бракованное (В),

в) по крайней мере, одно изделие стандартное (С).

Решение. а) Так как всего 37 изделий и выборка без упорядочивания, то общее число комбинаций находится как

.

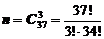Число комбинаций, благоприятствующих событию А равно

.

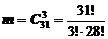Тогда вероятность события А равна

.

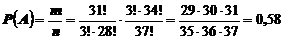б) Событие В противоположно событию А, поэтому

.

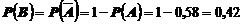в) Прежде, чем найти вероятность события С, найдем вероятность противоположного события 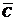- все три изделия бракованные

.

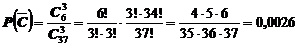Теперь легко найти вероятность события С, как

.

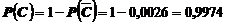Пример 11.Партия товара содержит 10 изделий. Из них 5 изделий стоят по 4 рубля, 3 изделия – по 1 рублю, 2 изделия – по 3 рубля. Найти вероятность того, что взятые наудачу два изделия стоят 5 рублей.

Решение. Обозначим искомое событие – А.

.

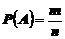Так как два изделия из десяти берутся без возвращения и без упорядочивания, то общее число комбинаций найдем как

.

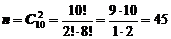Событие А состоится, если одно взятое изделие стоит 4 рубля, а другое – 1 рубль. Тогда число комбинаций, благоприятствующих событию А, находится по формуле (8)

.

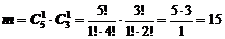Окончательно получим

.
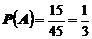