Способы устранения гетероскедастичности остатков регрессии. Метод взвешенных наименьших квадратов.

Гомоскедастичность - это предположение оттом, что дисперсии случайной ошибки 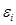является известной постоянной величиной для всех 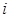наблюдений регрессионной модели.

Гетероскедастичность - означает предположение о дисперсии случайных ошибок регрессионной модели.

Вид преобразования зависит от того, известны или нет дисперсии отклонений .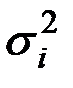

Устранение гетероскедастичности.

1) взвешенный метод наименьших квадратов - наблюдения с наименьшими дисперсиями получают наибольшие «веса», а наблюдения с наибольшими дисперсиями – наименьшие «веса». Поэтому наблюдения с меньшими дисперсиями отклонений будут более значимыми при оценке параметров регрессии, чем наблюдения с большими дисперсиями. При этом повышается вероятность получения более точных оценок.

Дисперсии известны:

2) взвешивание параметров регрессионной модели. Суть метода состоит в том, что отдельным наблюдениям независимой переменной с максимальным среднеквадратическим отклонением случайной ошибки придается больший вес, а остальным наблюдениям с минимальным среднеквадратическим отклонением случайной ошибки придается меньший вес. Благодаря этому оценки коэффициентов уравнения остаются эффективными. Модель регрессии при таком подходе называется взвешенной регрессией с весами .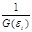

32. Способы устранения автокорреляции остатков регрессии. Авторегрессионное преобразование.

В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков должна быть устранена.

Устранить автокорреляцию остатков модели регрессии можно с помощью включения в модель автокорреляционного параметра, однако на практике данный подход реализовать весьма затруднительно, потому что оценка коэффициента автокорреляции является величиной заранее неизвестной.

Авторегрессионной схемой первого порядка называется метод устранения автокорреляции первого порядка между соседними членами остаточного ряда в линейных моделях регрессии либо моделях регрессии, которые можно привести к линейному виду.

Выборочный коэффициент остатков первого порядка рассчитывается по формуле:

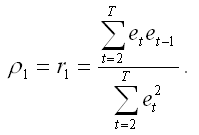
Важной проблемой при оценивании регрессии является автокорреляция остатков, которая говорит об отсутствии первоначально предполагавшейся их взаимной независимости. Автокорреляция остатков первого порядка, выявляемая с помощью статистики Дарбина-Уотсона, говорит о неверной спецификации уравнения либо о наличии неучтенных факторов. Естественно, для её устранения нужно попытаться выбрать более адекватную формулу зависимости, отыскать и включить важные неучтенные факторы или уточнить период оценивания регрессии.

В некоторых случаях, однако, это не даст результата, а отклонения еi просто связаны авторегрессионной зависимостью. Если это авторегрессия первого порядка, то её формула имеет вид еi=ei-1 + ui( - коэффициент авторегрессии, ||<1), и мы предполагаем, что остатки ui в этой формуле обладают нужными свойствами, в частности - взаимно независимы. Оценив , введем новые переменные уi=уi -yi-1; xi=xi -xi-1;^,.(это преобразование называется авторегрессионным, или преобразованием Бокса-Дженкинса)