Замещающие переменные в регрессионных моделях.

Замещающие переменные применяются вместо отсутствующих переменных.

Причины их использования:

· отсутствие данных,

· трудность измерения,

· неточные данные.

Отбрасывание существенной переменной приведет к смещенным и несостоятельным МНК-оценкам. Замещающая переменная может дать косвенную информацию о той самой существенной переменной, z – замещающая переменная.

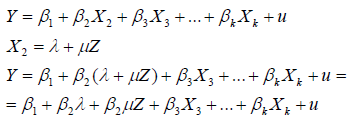
Например, исследуется вопрос об “утечке ” мозгов из страны А в страну В по показателю относительного уровня миграции трудовых ресурсов (М). Полагается, что при более высокой относительной разнице в заработной плате будет более высокой и миграция. Однако исследователь располагает данными только по ВВП на душу населения, а не по заработной плате. Поэтому вводится замещающая переменная G, которая является отношением ВВП страны В к ВВП страны А .

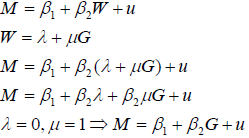
На практике обычно невозможно найти замещающую переменную, имеющую строгую линейную зависимость с недостающей переменной. Но если зависимость близка к линейной, то результаты приблизительно сохраняются. Основной проблемой является то, что не существует средств для проверки выполнения указанного условия.

Стандартизованный вид линейной модели множественной регрессии: форма записи и практическое применение. Как связаны стандартизованные коэффициенты регрессии с натуральными?

Построение модели множественной регрессии в стандартизированном или нормированном масштабе означает, что все переменные, включенные в модель регрессии, стандартизируются с помощью специальных формул.

Посредством процесса стандартизации точкой отсчёта для каждой нормированной переменной устанавливается её среднее значение по выборочной совокупности. При этом в качестве единицы измерения стандартизированной переменной принимается её среднеквадратическое отклонение.

Факторная переменная х переводится в стандартизированный масштаб по формуле:

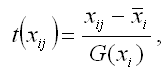
где xij – значение переменной xjв i-том наблюдении;

G(xj) – среднеквадратическое отклонение факторной переменной xi;

Результативная переменная у переводится в стандартизированный масштаб по формуле:

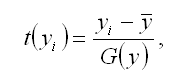
где G(y) – среднеквадратическое отклонение результативной переменной у.

Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результат, если соответствующий фактор х,- изменится на одну сигму при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии β_i сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.