Взаимодействие элементов в процессе функционирования сложной системы рассматривается как результат совокупного воздействия каждого элемента на все остальные.

При формализации процесса взаимодействия оно достаточно полно описывается в рамках механизма обмена сигналами.

Сигналы описывают входные и выходные воздействия и являются физическими носителями передаваемой между элементами информации.

1. Сигналы передаются по каналам связи, проложенным между элементами системы.

2. Действующие в реальной системе физические каналы связи вносят искажения и задержки по времени передачи сигналов.

3. Канал, передающий сигналы мгновенно и без искажения, называется идеальным.

4. Полностью и адекватно формализованная сложная система имеет только идеальные каналы связи.

5. Для описания физических каналов связи в модели вводятся эквивалентные элементы, отражающие возникающие искажения и задержки.

6. В результате введения каждого такого элемента возникает необходимость введения дополнительных идеальных каналов, соединяющий эквивалент с другими элементами.

Модель механизма обмена сигналами как формализованная (математическая) схема взаимодействия элементов системы между собой имеетследующие составляющие:

1. модель формирования выходных сигналов элементов системы;

2. модель сопряжения элементов сетью идеальных каналов связи;

3. модель приема входных сигналов для всех элементов системы.

В качестве математической схемы информационного взаимодействия необходимо рассматривать вторую составляющую механизма обмена сигналами – схему сопряжения элементов, определяющую адресацию характеристик выходных сигналов одних элементов и их компоновку во входные сигналы других элементов.

Математической схемой сопряжения элементов в системеS называется совокупность<X, Y, R >, а операторR называется оператором сопряжения.

Схема сопряжения<X, Y, R >содержит исчерпывающие сведения о модели взаимодействия и соединении элементов сложной системы.

Такая схема называется одноуровневойв том смысле, что она определяет прямое сопряжение элементов без учета их объединения в подсистемы или функциональные модули.

13.Основные типы систем массового обслуживания. Аналитическое решения для СМО М/М/1/0.

В ходе математической формализации систем как систем или сетей массового обслуживания (СМО) они традиционно представляются в виде композиции элементарных приборов обслуживания (Q-схем), соединенных в соответствии с имеющимися взглядами на облик системы.

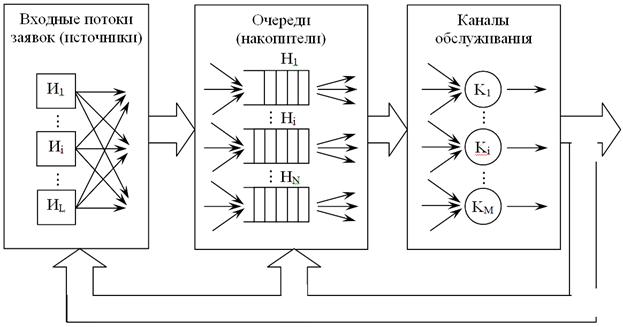
Обобщенная структурная схема СМО

Все СМО делятся на два больших класса:

разомкнутые СМО – функционирование источников и входной поток не зависят от процесса обслуживания (обратной связи нет);

замкнутые СМО –входной поток зависит от числа заявок, находящихся на обслуживании, а заявки с выхода могут опять поступать на вход системы (существует обратная связь).

Другие признаки классификации СМО:

1. По отсутствию или наличию возможности ожидания заявок в очередях выделяют: СМО с отказами; СМО с ожиданием; СМО смешанного типа, имеющие ограничения на время ожидания или на размеры очереди.

2. По количеству параллельно включаемых элементарных приборов обслуживания различают одноканальные и многоканальные СМО.

3. По числу этапов – фаз обслуживания заявок входного потока, реализуемых при последовательно включенных элементарных приборах обслуживания, выделяют однофазные и многофазные СМО.

4. По наличию специальных правил обслуживания различают СМО с приоритетными дисциплинами и бесприоритетными дисциплинами обслуживания (типа FIFO, LIFO).

Для определения СМО применяется специальная символика:

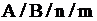
где 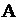– вид входного потока заявок или распределения интервалов между ними; 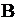– вид потока обслуживания или распределения длительности обслуживания; 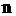– количество обслуживающих каналов; 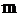– предельная длина очереди ( ).

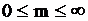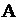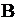Символы и/или принимают различные обозначения и определяют вид входного потока и потока обслуживания:

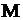– поток является пуассоновским и интервалы времени между заявками (событиями) имеют экспоненциальное распределение.

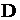– поток является детерминированными интервалы времени между событиями постоянны;

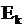– поток являетсяэрланговским ( 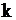-го порядка)и интервалы времени между заявками имеют распределение Эрланга( 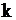-го порядка);

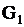– поток общего видас произвольным законом распределения интервалов времени между заявками (событиями).

Аналитической моделью СМОназывается совокупность уравнений и формул, позволяющих определять вероятности состояний системы в процессе ее функционирования в зависимости от времени и рассчитывать значения показателей эффективности по заданным параметрам входящего потока и потоков каналов обслуживания.

Рассмотрим примерпостроения такой модели для марковской одноканальной СМО с отказами типа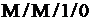 .Одной из возможных интерпретаций такой системы массового обслуживания является одноканальная телефонная линия.

На вход системы поступает пуассоновский поток заявок с интенсивностью

,

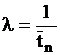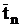– средний интервал времени между входящими заявками.

Каждая поступившая заявка обслуживается в течение времени 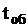(длительность разговора), распределенного по показательному закону. Интенсивность пуассоновского потока обслуживания равна

.

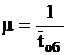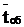– среднее время обслуживания заявки.

Требуется по известным значениям 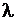, 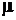определить вероятность обслуживания заявки в любой момент времени 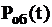, вероятность отказа в обслуживании 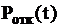, относительную 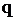и абсолютную 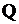пропускные способности системы.

При построении аналитических моделей СМО на основе уравнений Колмогорова используют визуальное представление системы в виде графа с вершинами, отвечающими состоянием СМО, и дугами, соответствующими разрешенным переходам.

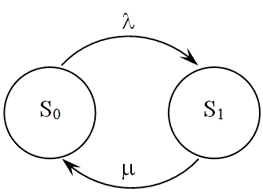
Графы состояний и переходов для систем массового обслуживания М/М/1/0

СМО вида 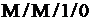может находиться в одном из двух состояний:

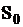– канал обслуживания свободен;

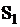– канал обслуживания занят.

Для любого момента времени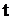

,

.

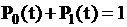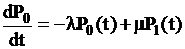
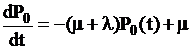Интегрирование последнего уравнения при начальном условии 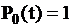дает решение

,

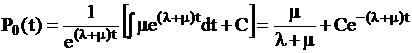где C-константа. С учетом начальных условий можно получить

, , .

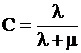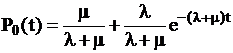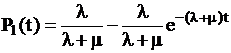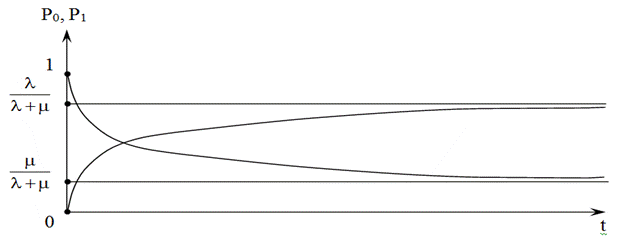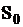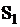Зависимости вероятностей пребывания СМО в состояниях и от времени

Вероятность обслуживания заявки, поступившей в момент времени 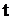равна 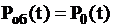, вероятность отказа в обслуживании равна 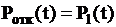, относительная пропускная способность системы равна 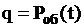, абсолютная пропускная способность равна .

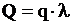При 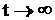СМО переходит в установившейся режим работы

, .

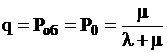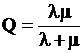14.Сущность метода имитационного моделирования применительно к исследованию СМО. Потоки событий и их характеристики (1,2,3,7).

Реализация технологий имитационного моделирования применительно к задачам исследования СМО предполагает:

1) построение алгоритмов и программных модулей, вырабатывающих реализации случайных потоков однородных и неоднородных событий – «генераторов» источников;

2) построение моделирующих алгоритмов и программных модулей, описывающих функционирование отдельных элементов, а также СМО в целом в соответствии с ее структурой и внутренними параметрами;

3) многократное воспроизведение входных потоков и общего процесса обслуживания, а также обработку получаемых данных в интересах оценки показателей эффективности данного типа СМО.

Элементы СМО разделяют на активные, пассивные и активно-пассивные.

Активными элементами называются такие, смена состояний которых обусловлена только их внутренними свойствами.

Пассивныминазываются такие элементы, которые изменяют свои свойства только под воздействием активных элементов, а, в общем случае, любых внешних факторов.

Активно-пассивными элементами называются такие, которые в одном из своих возможных состояний являются активными, а в других – пассивными.

Активные элементы – источники заявок.

Пассивные элементы – накопители заявок.

Активно-пассивные элементы – каналы обслуживания заявок.

Простейший поток

Поток, для которого одновременно выполняются свойстваординарности, отсутствия последействия, стационарности называется простейшим.

Простейший поток занимает центральное место в теории СМО.Для простейшего потока

, ,

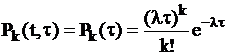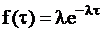имеет место пуассоновский закон распределения числа событий и показательный закон распределения интервалов между событиями.

Важность простейшего (пуассоновского) потока обусловлена следующим: согласно предельной теореме сумма большого числа независимых потоков с произвольным законом распределения интервалов между событиями стремится к простейшему с ростом числа слагаемых.

Поток Пальма

Поток Пальма характеризуется свойствами стационарности, ординарности и ограниченного последействия. Важными для практики образцами потока Пальма являются потоки Эрланга различных порядков.

Потоком Эрланга порядка 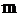называется поток, образуемый из простейшего в результате «просеивания» последнего, когда выбрасываются все точки за исключением 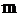-ой. Для такого потока закон распределения интервалов имеет вид

,

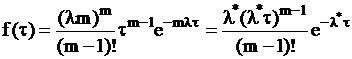где 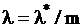– интенсивность потока Эрланга, а 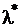– интенсивность исходного потока Пуассона. Простейший поток является частным случаем потока Эрланга при .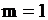