Табличный метод генерации нормально распределенных чисел

Для этого нормальное число можно взять из справочника в таблице функции Лапласа и получить случайное число по методу взятия обратной функции: x = F^–1(r), где F – интегральная функция Лапласа.

Технически это означает, что надо разыграть случайное равномерно распределенное число r из интервала [0; 1] стандартным ГСЧ, найти равное ему число в таблице значений функции Лапласа в столбце F и по строке определить случайную величину x, соответствующую этому числу.

Недостатком метода является необходимость хранения в памяти компьютера всей таблицы чисел функции Лапласа.

Метод генерации нормально распределенных чисел, использующий центральную предельную теорему

Общая идея метода следующая: требуется сложить случайные числа с любым законом распределения, нормализовать их и перевести в нужный диапазон нормального распределения.

Допустим, что нам надо в целях имитации получить ряд случайных чисел x, распределенных по нормальному закону с заданными математическим ожиданием m_x и среднеквадратичным отклонением σ_x.

1. Сложим n случайных чисел, используя стандартный ГСЧ:

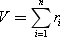
Согласно ЦПТ числа V образуют ряд значений, распределенный по нормальному закону. Эти числа тем лучше описывают нормальный закон, чем больше параметр n. На практике n берут равными 6 или 12. Заметим, что закон распределения чисел V имеет математическое ожидание m_V = n/2, σ_V = sqrt(n/12). Поэтому он является смещенным относительно заданного произвольного.

2. С помощью формулы z = (V – m_V)/σ_V нормализуем этот ряд. Получим нормализованный закон нормального распределения чисел Z. То есть m_z = 0, σ_z = 1.

3. Формулой (сдвиг на m_x и масштабирование на σ_x) преобразуем ряд Z в ряд x: x = z · σ_x + m_x.

Пример. Смоделировать поток заготовок для обработки их на станке. Известно, что длина заготовки колеблется случайным образом. Средняя длина заготовки составляет 35 см, а среднеквадратичное отклонение реальной длины от средней составляет 10 см. То есть по условиям задачи m_x = 35, σ_x = 10. Тогда значение случайной величины будет рассчитываться по формуле: V = r₁ + r₂ + r₃ + r₄ + r₅ + r₆, где r – лучайные числа из ГСЧ_рр [0; 1], n = 6.
X = σ_x · (sqrt(12/n) · (V – n/2)) + m_x = 10 · sqrt(2) · (V – 3) + 35
или
X = 10 · sqrt(2) · ((r₁ + r₂ + r₃ + r₄ + r₅ + r₆) – 3) + 35.

Метод Мюллера

Совсем простым методом получения нормальных чисел является метод Мюллера, использующий формулы: Z = √(–2 · Ln(r₁)) · cos(2π · r₂), где r₁ и r₂ – случайные числа из ГСЧ_рр [0; 1].

Можно также воспользоваться аналогичной формулой Z = √(–2 · Ln(r₁)) · sin(2π · r₂), где r₁ и r₂ — случайные числа из ГСЧ_рр [0; 1].

Пример. Материал поступает в цех один раз в сутки по 10 штук сразу. Расход материала из цеха случайный по нормальному закону с математическим ожиданием m = 10 и среднеквадратичным отклонением σ = 3.5. Вычислить вероятность дефицита на складе при запасе материала в начальный момент времени 20 штук.

При реализации в среде моделирования Stratum решение задачи будет выглядеть следующим образом.

z := sqrt(–2 · ln(rnd)) · cos(2 · PI · rnd) x := σ · z + m запас := запас + 10 запас := (запас – x) · ed(запас – x) дефицит := дефицит + not(ed(запас – x)) N := N + 1 P := дефицит/N stop(N > k)

z — нормальное нормализованное случайное число; x — нормальное число, ежедневный расход материалов; запас — состояние склада: начало дня, моделирование прихода; запас — состояние склада: конец дня, моделирование расхода; дефицит — счетчик дней, в течение которых наблюдался дефицит; N — количество дней; P — вероятность дефицита; k — моделирование в течение k дней.

p(x) = 1/(x * normal_sigma * sqrt(2*pi)) * exp( -(log(x)-normal_mean)² / (2*normal_sigma²) ) для x > 0, где normal_mean = log(mean²/sqrt(sigma² + mean²)) и normal_sigma = sqrt(log(1 + sigma²/mean²)). Другими словами, "логарифмически-нормальный закон" встречается у случайных чисел, логарифм которых распределен нормально. Это распределение широко используется в теории надежности; с его помощью аппроксимируются распределения полей атмосферных и промышленных помех.

5) с логнормальным распределением:

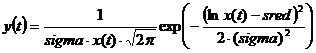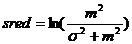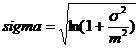, где , , где 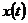– случайный процесс с равномерным распределением в диапазоне [0,1].