Создание генераторов потоков случайных событий

На рисунке 4.1 приведен алгоритм моделирования потоков события во времени по распределению Пуассона. На рисунке 4.2 приведен простейший генератор, моделирующий потоки событий во времени по распределению Пуассона, созданный средствами объектного моделирования Simulink.

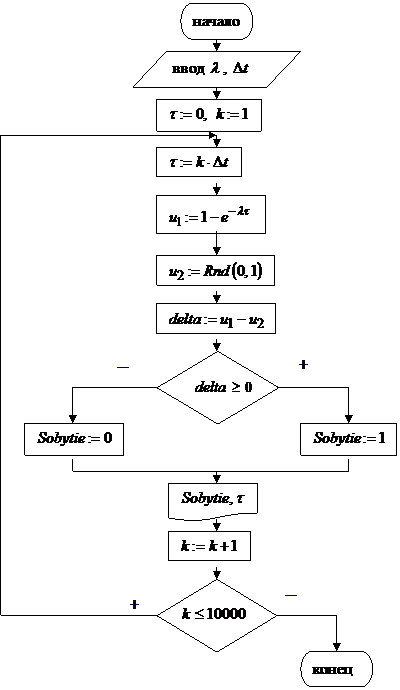
Рисунок 4.1. – Алгоритм моделирования потоков событий во времени по распределению Пуассона

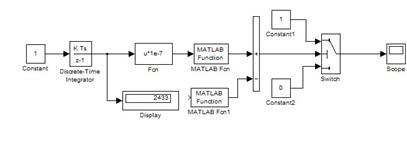
Рисунок 4.2. – Генератор, созданный средствами Simulink и моделирующий потоки событий во времени по распределению Пуассона

Генератор работает следующим образом. Задаются исходные данные: шаг во времени 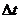, постоянная распределения Пуассона 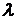, число циклов 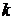. В цикле рассчитывается текущее время 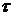, определяется с течением времени функция распределения Пуассона 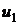и в диапазоне 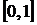генерируется равномерно распределенное случайное число 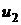. Находится разность 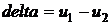. Проверяется условие: если 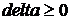, то величине 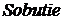присваивается 1, иначе этой величине присваивается ноль. Значение 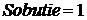означает, что во времени 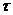произошло событие, имеющее распределение Пуассона для интервалов между событиями. Результаты выводятся на печать и визуализируются в виде временного ряда нулей и единиц. Далее проводятся вычисления цикле до тех пор, пока не достигнут конец временного интервала, например, .

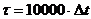Порядок выполнения

1. Разработать генераторы потоков случайных событий, имеющих заданное распределение согласно варианта.

2. Выполнить имитацию общего потока случайных событий, представляющего собой сумму потоков однородных событий согласно варианта.

3. Провести анализ статистических характеристик полученного потока.

4. Вывести результаты в виде графиков и массивов данных.

Варианты заданий

Ва-ри-ант	Виды законов распределений потоков случайных событий
Пуассона	Нестационар-ный Пуассона	Поток Эрланга	Поток Пальма	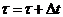Регулярный поток
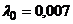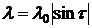			второго порядка	–	событие генерируется на каждом 10-ом шаге
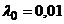		–	четвер-того порядка	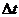генерируется по закону Вейбулла	событие генерируется при достижении коси-нусоидой значения 1/2
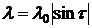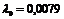	–	,	третьего порядка	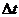генерируется по показательному закону	событие генерируется при достижении сину-соидой значения 0
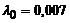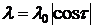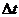			–	генерируется по Релеевскому закону	событие генерируется на каждом 7 и 9 шаге
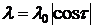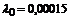	–		нулевого порядк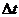а	генерируется по закону Вейбулла	событие генерируется при достижении коси-нусоидой значения 1
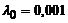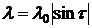			седьмого порядка	–	событие генерируется при достижении сину-соидой значения 1/2
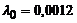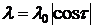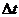			–	генерируется по нормальному закону	событие генерируется при достижении коси-нусоидой значения -1/2
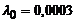		–	нулевого порядка	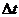генерируется по показательному закону	событие генерируется на каждом 3 и 4 шаге
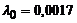		–	шестого порядка	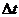генерируется по показательному закону	событие генерируется на каждом 5 и 34-ом шаге
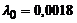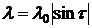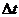			–	генерируется по показательному закону	событие генерируется на каждом 37-ом шаге
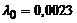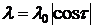			восьмого порядка	–	событие генерируется при достижении коси-нусоидой значения 1/3
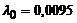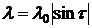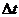			–	генерируется по Релеевскому закону	событие генерируется при достижении си-нусоидой значения 1/5
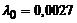		–	второго порядк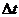а	генерируется по закону Вейбула	событие генерируется на каждом 7-ом шаге
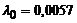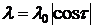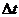			–	генерируется по равномерному закону	событие генерируется при достижении коси-нусоидой значения 0
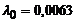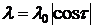			девятого порядка	–	событие генерируется на каждом 13-ом шаге
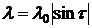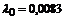	–		13-ого порядка	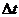генерируется по показательному закону	событие генерируется при достижении си-нусоидой значения 1/8
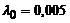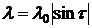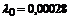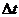			–	генерируется по Релеевскому закону	событие генерируется при достижении си-нусоидой значения -1/8
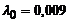		–	15-ого порядк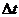а	генерируется по закону Вейбула	событие генерируется на каждом 3-ем шаге
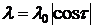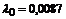	–		нулевого порядка	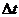генерируется по показательному закону	событие генерируется при достижении си-нусоидой значения -1/2
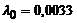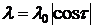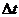			–	генерируется по Релеевскому закону	событие генерируется при достижении си-нусоидой значения -1
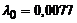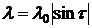			двадца-того порядка	–	событие генерируется при достижении коси-нусоидой значения -1
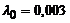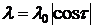			пятого порядка	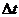генерируется по закону Вейбула	–
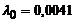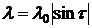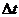			–	генерируется по Релеевскому закону	событие генерируется на каждом 6-ом шаге

4.5 Контрольные вопросы

1. Основные свойства простейшего потока?

2. Что описывает закон распределения Пуассона?

3. Что представляет собой последействие в случайном потоке?

4. Каковы особенности потока Пальма?

5. Каким образом можно получить поток Эрланга 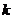-го порядка?

4.6 Рекомендуемая литература

1. Е.В. Вентцель. Теория вероятностей. М.: наука, 1969. – 576 с.

2. Е.И. Гурский. Теория вероятностей с элементами математической статистики: уч. пос. для вузов. – М.: Вс. шк., 1971. – 328 с.

3. В.М. Дрибан, Г.Г. Пенина. Теория вероятностей. Уч. пос. – Донецк: ДонГУЭТ, 2003. – 519 с.

4. И.И. Гихман, А.В. Скороход. Введение в теорию случайных процессов. М.: наука, 1971. – 664 с.

Лабораторная работа № 5