Вероятностные модели случайных потоков событий

Цель работы: изучение моделей случайных потоков; анализ статистических характеристик случайных потоков; имитационное моделирование простейших потоков событий.

Общие положения

Под потоком событий в теории случайных процессов понимается последовательность событий, происходящих одно за другим в какие-то моменты времени. Примерами могут служить: поток вызовов на телефонной станции; поток включений приборов в бытовой электросети; поток заказных писем, поступающих в почтовое отделение; поток сбоев (неисправностей) персонального компьютера; поток выстрелов, направляемых на цель во время стрельб и т.п. События, образующие поток, в общем случае могут быть различными, но чаще всего рассматривают потоки однородных событий, различающихся только моментами появления во времени.

Рассмотрим потоки событий, обладающие некоторыми особенно простыми свойствами. Среди таких потоков следует выделить стационарные потоки событий.

Поток событий называется стационарным, если вероятность попадания того или иного числа событий на участок времени протяженностью 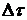зависит только от длины участка и не зависит от того, где именно на оси времени расположен этот участок.

Поток событий называется потоком без последействия, если для любых неперекрывающихся участков времени число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие участки.

Поток событий называется ординарным, если вероятность попадания на элементарный участок 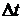двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события.

Если поток событий обладает всеми тремя свойствами (т.е. стационарен, ординарен и не имеет последействия), то он называется простейшим (или стационарным пуассоновским) потоком. Название “пуассоновский” связано с тем, что при соблюдении условий 1 – 3 число событий, попадающих на любой фиксированный интервал времени, будет распределено по закону Пуассона.

Простейший (пуассоновский поток).

Вероятность наступления 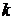событий за время 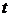для закона распределения Пуассона определяется по следующей формуле:

,

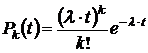где 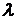– интенсивность случайного потока, т.е. среднее число событий (поступающих заявок) в единицу времени.

Плотность распределения временного интервала 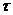между заявками в простейшем пуасоновском потоке соответствует экспоненциальному закону распределения:

, .

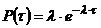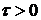В свою очередь функция распределения имеет вид:

.

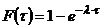Нестационарный пуассоновский поток.

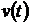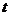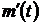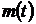Если поток обладает свойствами ординарности и отсутствия последствия, но не является стационарным, то он называется нестационарным пуассоновским потоком. Плотность такого потока – переменная величина, которая в точке , по определению, равна производной , где – математическое ожидание числа событий на участке .

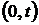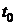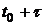Можно показать, что для такого потока вероятность появления за время от до ровно 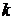событий равна:

,

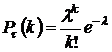где .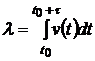

Таким образом, 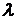является математическим ожиданием числа событий на участке от 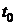до 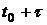, а само это число событий подчиняется закону Пуассона. Таким образом, нестационарный пуассоновский поток сводится к стационарному пуассоновскому потоку.

Поток Пальма.

Ординарный поток называется потоком Пальма (потоком с ограниченным последействием), если промежутки времени между любыми двумя последовательными событиями являются независимыми случайными величинами. Примером потока Пальма может служить поток деталей, обтачиваемых токарем, если время изготовления каждой очередной детали не зависит от времени изготовления всех предыдущих деталей.

В простейшем потоке вследствие отсутствия последствия все интервалы между двумя соседними событиями представляют собой независимые случайные величины, поэтому простейший поток является частным случаем стационарного потока Пальма. Это свойство потока Пальма играет большую роль в тех случаях, когда необслуженные заявки вновь поступают в другую систему обслуживания.

Потоки Эрланга.

Потоки Эрланга получаются путем особого преобразования (“разрежения”) простейшего потока. Это преобразование состоит в выбрасывании из простейшего потока некоторых событий.

Выбросим из простейшего потока каждое второе событие, т.е. 2-е, 4-е, 6-е и т.д. Оставшиеся события образуют новый поток, который называется потоком Эрланга 1-го порядка. Очевидно, что интервалы между соседними событиями потока Эрланга 1-ого порядка получаются суммированием двух интервалов между соответствующими событиями простейшего потока.

Поток Эрланга 2-го порядка образуется следующим образом. Выбросим два события после первого, затем два события после оставшегося четвертого, затем два события после оставшегося седьмого и т.д. Интервалы между соседними событиями потока Эрланга 2-ого порядка представляет собой сумму трех интервалов между соответствующими событиями простейшего потока.

Вообще, поток Эрланга 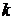-го порядка получается из простейшего потока путем выбрасывания по 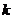событий после оставшегося (первое событие не выбрасывается).

Простейший поток можно рассматривать как поток Эрланга нулевого порядка.

Для потока Эрланга 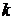-го порядка:

.

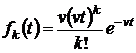
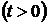Закон распределения с такой плотностью вероятности называется законом Эрланга 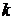-го порядка. Он представляет собой закон распределения суммы 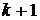независимых случайных величин, имеющих показательное распределение с одним и тем же параметром .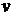