Качественный анализ технических систем. Необходимость выполнения качественного анализа технических систем, его цели.

Моделирование нелинейных систем: определение нелинейной системы, виды нелинейных характеристик элементов технических систем.

Особенности поведения и анализа нелинейных систем, методы решения систем нелинейных ДУ.

Модели нелинейных систем на фазовой плоскости. Анализ технических систем по фазовому портрету. Примеры построения фазовых портретов.

Совершенно так же, как и в линейной системе, процесс регулирования, описываемый уравнениями, содержащими нелинейности, может быть представлен на фазовой плоскости или в фазовом пространстве.

Рассмотрим и здесь в качестве основного примера случай, когда движения описываются двумя дифференциальными уравнениями первого порядка:

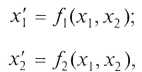
гдеf₁(x₁, х₂) и f₂(х₁,х₂) — заданные, в общем случае нелинейные функции указанных аргументов.

Дифференциальное уравнение фазовых траекторий получается, если вместо производных по времени ввести производнуюdx₁/dx₂.

Получаем:

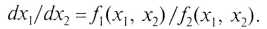
К фазовой траектории может быть проведена только одна касательная, и, следовательно, фазовые траектории не пересекаются во всех тех точках фазовой плоскости, где не обращаются одновременно в нуль f₁(х₁, x₂) и f₂(х₁, х₂). Особые точки системы находятся из условия dx₁/dx₂ = 0/0, то есть определяются как общие корни двух уравнений:

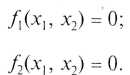
В предыдущем случае при рассмотрении линейной системы было:

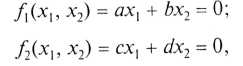
и уравнения имели только одно общее решение: х₁ = х₂ =0. В плоскости х_1, х₂ этм условия в случае линейной системы определяют две прямые линии, пересекающиеся в начале координат (рис.1, а). Если же функции f₁(х₁, x₂) и f₂(х₁, х₂) нелинейны, то кривые, соответствующие уравнениям, могут пересекаться и вне начала координат. Система имеет в этом случае, кроме ре­шения х₁, =х₂ = 0, и другие решения. В этом случае, кроме регулируемого режима, соответствующего началу координат, в системе возможны и иные положения равновесия (рис.1, б), и характер движения в системе зависит от величины отклонения от начала координат, вызванного возмущением.

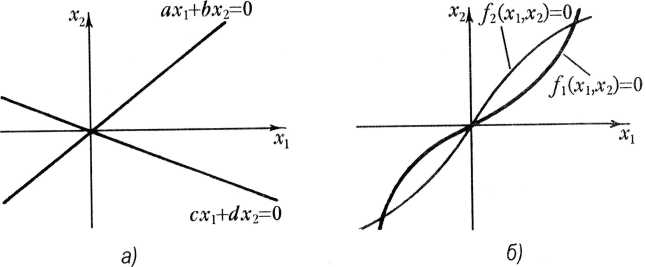
Рис.1 Графики, соответствующие уравнениям для линейной (а) и нелинейной (б) систем

В рассматриваемом нелинейном случае особые точки могут быть лишь тех же типов, что и в линейной системе (фокусы, узлы и седла). Чтобы в нелинейном случае определить тип особой точки, надо составить соответствующее этой особой точке уравнение линейного приближения, разложив в окрестности этой точки в ряды правые части уравнений и сохранив затем в этих рядах только линейные члены. Эта операция эквивалентна «локальной» линеаризации системы вблизи особой точки.

Факторные модели и модели регрессионного анализа. Примеры реализации.

С помощью факторного анализа возможно выявление факторов, отвечающих за наличие линейных статистических связей корреляций между наблюдаемыми переменными.

Таким образом, можно выделить две цели факторного анализа:

• определение взаимосвязей между переменными, их классификация, т. е. «объективная R-классификация»;
• сокращение числа переменных.

Для выявления наиболее значимых факторов и, как следствие, факторной структуры, наиболее оправданно применять метод главных компонентов. Суть данного метода состоит в замене коррелированных компонентов некоррелированными факторами. Другой важной характеристикой метода является возможность ограничиться наиболее информативными главными компонентами и исключить остальные из анализа, что упрощает интерпретацию результатов. Достоинство данного метода также в том, что он – единственный математически обоснованный метод факторного анализа.

Факторный анализ – методика комплексного и системного изучения и измерения воздействия факторов на величину результативного показателя. Существуют следующие типы факторного анализа:

1. Детерминированный (функциональный) – результативный показатель представлен в виде произведения, частного или алгебраической суммы факторов.

2. Стохастический (корреляционный) – связь между результативным и факторными показателями является неполной или вероятностной.

3. Прямой (дедуктивный) – от общего к частному.

4. Обратный (индуктивный) – от частного к общему.

5. Одноступенчатый и многоступенчатый.

6. Статический и динамический.

7. Ретроспективный и перспективный.

Обязательные условия факторного анализа:

• Все признаки должны быть количественными;
• Число признаков должно быть в два раза больше числа переменных;
• Выборка должна быть однородна;
• Исходные переменные должны быть распределены симметрично;
• Факторный анализ осуществляется по коррелирующим переменным.

· По характеру взаимосвязи между показателями различают методы детерминированного и стохастического факторного анализа

· Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, т. е. когда результативный показатель факторной модели представлен в виде произведения, частного или алгебраической суммы факторов.

Стохастический анализ представляет собой методику исследования факторов, связь которых с результативным показателем в отличие от функциональной является неполной, вероятностной (корреляционной). Если при функциональной (полной) зависимости с изменением аргумента всегда происходит соответствующее изменение функции, то при корреляционной связи изменение аргумента может дать несколько значений прироста функции в зависимости от сочетания других факторов, определяющих данный показатель.

Регрессионная модель 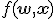— это параметрическое семейство функций, задающее отображение

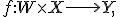
где 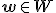— пространтсво параметров, 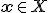— пространство свободных переменных, 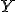— пространство зависимых переменных.

Регрессионная модель объединяет широкий класс универсальных функций, которые описывают некоторую закономерность. При этом для построения модели в основном используются измеряемые данные, а не знание свойств исследуемой закономерности.

Примеры регрессионных моделей: линейные функции, алгебраические полиномы, ряды Чебышёва, нейронные сети без обратной связи, например, однослойный персептрон Розенблатта, радиальные базисные функции и прочее.