Модель Леонтьева межотраслевого баланса

В заключение рассмотрим одну из макроэкономических моделей (т.е. модель, описывающую экономику в целом), а именно модель Леонтьева (Василий Леонтьев (1906-1998) – выдающийся экономист русского происхождения, лауреат Нобелевской премии). Предположим, что наша экономика состоит из 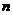отраслей. Пусть 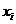− общий (валовой) объём производства 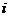-й отрасли, например, за год. Отрасли в процессе производства потребляют продукцию друг друга; пусть 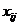− объём продукции 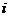-й отрасли, потребляемый 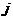-й отраслью в процессе производства. Мы предполагаем, в частности, что величина 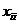может быть ненулевой; т.е. возможно производственное потребление продукта 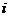-й отрасли внутри самой этой отрасли. Пусть теперь 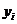− объём продукта 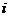-й отрасли, поставляемый потребителю. Тогда мы имеем соотношения баланса

.

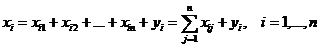Введём так называемые коэффициенты прямых затрат 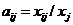, показывающие сколько единиц продукции 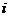-й отрасли необходимо для производства одной единицы продукции 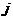-й отрасли (они полностью аналогичны технологическим коэффициентам из раздела 2). Они определяются технологиями производства в отраслях, поэтому мы будем считать их постоянными. Тогда имеем 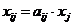, и соотношения баланса можно переписать в виде

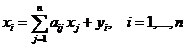(14.1)

Заметим, что по экономическому смыслу мы имеем 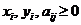при всех значениях индексов. Перепишем для краткости систему (14.1) в матричном виде, вводя векторы-столбцы валового производства 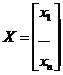и потребления 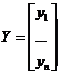, а также матрицу прямых затрат :

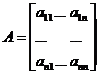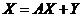(14.2)

Теперь возникает вопрос: в состоянии ли данная экономика удовлетворить произвольный спрос 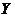или же она в значительной степени работает «сама на себя» (что имело место в истории нашей страны)? Математически этот вопрос можно переформулировать так: верно ли, что для любого неотрицательного вектора потребления 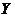существует неотрицательный вектор объёмов производства 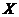, обеспечивающий данное потребление в силу уравнения (14.2)? Разумеется, верно это или неверно определяется матрицей .

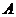Определение. Неотрицательная матрица 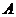(т.е. матрица, все элементы которой неотрицательны) называется продуктивной, если для любого вектора 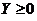существует решение 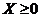уравнения (14.2). В этом случае и нашу экономику мы назовём продуктивной.

Как же узнать, является ли матрица продуктивной или нет?

Утверждение 1. Матрица 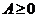является продуктивной тогда и только тогда, когда матрица 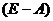имеет обратную и эта обратная матрица неотрицательна: 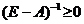. Здесь 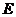−единичная матрица размера .

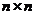Доказательство. Уравнение (14.2) можно переписать в эквивалентной форме

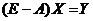. (14.3)

Поэтому, если матрица 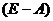имеет неотрицательную обратную, то последнее уравнение однозначно разрешимо и решение имеет вид

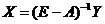. (14.4)

Поскольку вектор 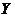и матрица 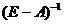неотрицательны, то, очевидно, и 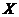в формуле (14.4) будет неотрицательным. Тем самым, матрица 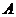продуктивна.

Обратно, допустим, что матрица 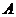является продуктивной. Тогда уравнение (14.3) имеет решение для каждого неотрицательного вектора 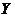. Возьмём в качестве 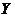неотрицательный вектор 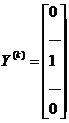, в котором единица стоит на 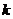-м месте. Тогда найдётся неотрицательное решение 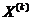соответствующего уравнения (14.3). Составим 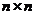матрицу 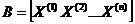из этих столбцов. Ясно, что она будет неотрицательной. Кроме того, из определения умножения матриц легко увидеть, что

.

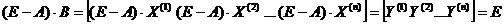Отсюда следует, что матрица 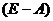имеет обратную, равную 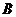, которая неотрицательна. Утверждение полностью доказано.

Данное утверждение не всегда просто проверить, т.к. нахождение обратной матрицы представляет значительную трудность для матриц больших размеров. Поэтому были найдены более простые достаточные условия продуктивности. Приведём без доказательства одно из них:

Утверждение 2. Если сумма элементов каждой строки матрицы 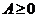меньше единицы

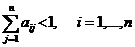, то матрица 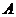продуктивна.

Приведём пример. Следующая матрица в силу утверждения является продуктивной:

.

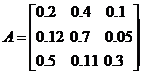Матрица 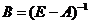имеет ясный экономический смысл. В самом деле, её 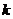-й столбец 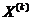, полученный при доказательстве утверждения 1, показывает объёмы производства отраслей, необходимые для поставки потребителю одной единицы продукции 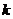-й отрасли. Исходя из этого, матрицу 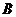называют матрицей полных затрат, а её элементы – коэффициентами полных затрат.

Рассмотрим подробно конкретный пример. Пусть для простоты в нашей экономике имеются две отрасли, и матрица прямых затрат имеет вид:

.

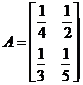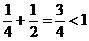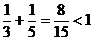Поскольку и , в силу утверждения 2 очевидно, что данная матрица продуктивна. В данном случае в этом можно убедиться и непосредственно в силу утверждения 1, вычисляя

.

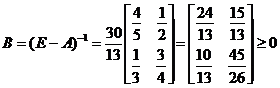Эта матрица является матрицей полных затрат. Например, чтобы поставить потребителю за один год одну единицу продукции первой отрасли, надо, чтобы валовый объём первой отрасли равнялся 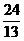единиц, а второй отрасли – 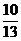единиц (естественно, мы считаем продукцию обеих отраслей бесконечно делимой). А чтобы поставить потребителю за тот же период единицу продукции второй отрасли, надо, чтобы валовый объём первой отрасли равнялся 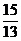единиц, а второй отрасли – 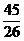единиц.

Решим теперь, например, такую задачу: каковы должны быть валовые объёмы производства отраслей, чтобы обеспечить ежегодно для потребителя 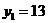единиц продукции первой отрасли и 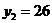единиц второй. Расписывая подробнее формулу (14.4) и используя вычисленную матрицу полных затрат, получаем искомые объёмы

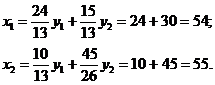
Пусть теперь нам известны прямые затраты электроэнергии и трудовых ресурсов на выпуск единицы продукции каждой отрасли (т.е. внутренние затраты в самой отрасли, обусловленные технологией производства):

	1-я отрасль	2-я отрасль
Эл.энергия, КВт ч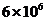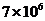
Труд.ресурсы, Чел.-часов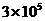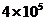

Подчитаем теперь, например, полные энергозатраты на выпуск одной единицы продукции отраслей (т.е. затраты, учитывающие взаимосвязи и усилия всех отраслей). Для первой отрасли эта величина составляет:

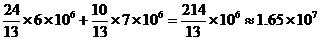(КВт ч),

а для второй

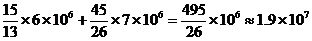( КВт ч).

Аналогично можно подсчитать и полные затраты труда на выпуск одной единицы продукции каждой отрасли. Для первой отрасли это

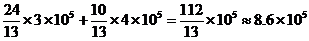(человеко-часов),

а для второй

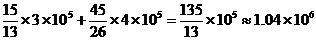(человеко-часов).

Литература

1. Н. Ш. Кремер. Исследование операций в экономике – М.: «Банки и биржи», 1997.
2. Г. И. Просветов. Математические методы в экономике – М.: Издательство РДЛ, 2005.
3. В. И. Малыхин. Математика в экономике – М.: ИНФРА-М, 2001.
4. О. О. Замков, Ю. А. Черемных, А. В. Толстопятенко. Математические методы в экономике – М.: «Дело и сервис», 1997.