Теоремы двойственности, их применение

Оптимальные значения и оптимальные решения взаимно-двойственных задач тесно связаны друг с другом. Эти связи описываются в теоремах двойственности. Разъясним их на примере задачи торга, рассмотренной выше. Для этого решим симплекс-методом двойственную задачу. Всех деталей мы приводить не будем; отметим только, что сначала мы заменяем неравенства-ограничения равенствами с помощью введения двух дополнительных переменных 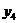и :

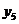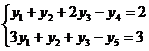
На первом шаге дополнительные переменные берём в качестве базисных, затем выполняем шаги как было рассмотрено выше; и, наконец, на последнем шаге базисными оказываются переменные 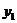и 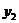, а свободными – 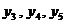. При этом целевая функция выражается через свободные переменные последнего шага так:

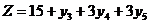, (7.1)

а соответствующее базисное решение имеет вид:

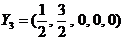. (7.2)

В силу неотрицательности всех коэффициентов при переменных в формуле (7.1) мы заключаем, что базисное решение (7.2) является оптимальным с оптимальным значением .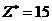

Это оптимальное значение в точности совпадает с оптимальным значением исходной задачи (2.1)-(2.2). Совпадение это не является случайным, а имеет место всегда, как утверждает

Теорема (первая теорема двойственности).Если для одной из взаимно-двойственных задач существует оптимальное решение, то и для двойственной ей задачи оптимальное решение имеется; при этом оптимальные значения целевых функций совпадают. Если целевая функция одной из задач не ограничена (в соответствующую сторону), то ограничения двойственной ей задачи несовместны.

Таким образом, найдя оптимальное значение для одной из взаимно-двойственных задач, мы автоматически узнаём оптимальное значение для другой.

Оказывается, что и оптимальное решение задачи линейного программирования мгновенно находится, если мы решили (симплекс-методом) двойственную ей задачу. Рассмотрим это явление на примере пары взаимно-двойственных задач (2.1)-(2.2) и (6.1)-(6.2). Заметим, что после введения дополнительных переменных и перехода к ограничениям-равенствам в обеих задачах мы имеем по 5 переменных: , , .., и 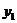, , 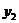.. . 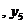Обратите внимание, что в первой задаче мы имеем две первоначальные переменные и три дополнительные, а во второй наоборот – три первоначальные и две дополнительные. Поэтому естественным образом возникает следующее соответствие между переменными наших двух задач:

переменные задачи (2.1)-(2.2)
первоначальные	дополнительные
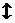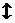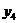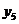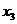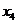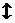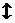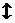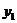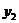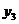дополнительные	первоначальные
переменные задачи (6.1)-(6.2)

(7.3)

Подпишем теперь соответственно выше и ниже этих переменных их значения для оптимальных решений обеих задач и сопоставим эту картинку с выражениями целевых функций через свободные переменные на последнем шаге симплекс-метода для соответствующей задачи (в этих выражениях мы переставили (для наглядности) слагаемые и добавили формально базисные переменные с нулевыми коэффициентами):

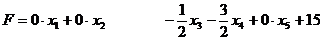(3, 3, 0, 0, 1)
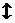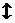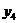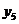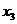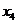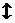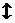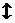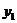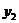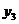(0, 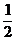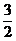0, , , 0)

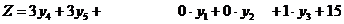(7.4)

Таблица (7.4) ясно и наглядно иллюстрирует следующее общее свойство:

Теорема (вторая теорема двойственности). Компоненты оптимального решения задачи линейного программирования равны абсолютным значениям коэффициентов при соответствующих (в силу соответствия типа (7.3)) переменных в выражении целевой функции двойственной ей задачи через свободные переменные на заключительном шаге симплекс-метода (при этом добавляются формально и базисные переменные с нулевыми коэффициентами).

Формулировка этой теоремы неизбежно тяжеловата, но для её понимания надо просто внимательнее изучить пример в таблице (7.4).

Из первой и второй теорем двойственности ясно, что, решая симплекс-методом одну из двух взаимно-двойственных задач, мы автоматически получаем оптимальное значение и оптимальное решение для другой. А отсюда и возможное практическое применение: если нам необходимо решить задачу линейного программирования, то бывает, что проще решить двойственную ей задачу (например, если для двойственной задачи возможно графическое решение из разд. 3), а затем по описанному рецепту автоматически найти решение исходной нашей задачи. Данные способ носит название двойственного симплекс-метода.

В завершение данного раздела рассмотрим третью теорему двойственности. Для этого ещё раз обратимся к задаче на оптимальное использование ресурсов (2.1)-(2.2). Разумно рассмотреть более общую задачу, когда доступные нам ежесуточно объёмы ресурсов могут меняться от квартала к кварталу или от года к году. Разумеется, можно каждый раз при таком изменении заново решать задачу линейного программирования. Но оказывается, что применение двойственной задачи позволяет избежать этого, по крайней мере, при небольших изменениях объёмов ресурсов. В самом деле, предположим, что мы решили исходную задачу (2.1)-(2.2) двойственным симплекс-методом, получив выражение (6.1) и оптимальное решение (6.2). Теперь рассмотрим обобщённую задачу типа (2.1)-(2.2), в которой доступные ежесуточно объёмы сырья 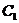, , 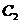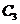составляют 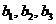единиц соответственно. Будем считать, что 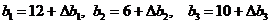; где величины 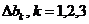− небольшие.

Будем решать обобщённую задачу также двойственным симплекс-методом. Заметим, что при этом допустимое множество в двойственной задаче будет тем же самым, и только целевая функция изменится на следующую (см. таблицу (6.3)):

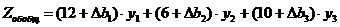(7.5)

В силу наглядных геометрических соображений графического метода (для теоретических рассмотрений он годится для любого числа переменных и выглядит практически так же как в разд. 3) ясно, что для небольших 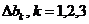оптимальное решение будет тем же самым, а именно (7.2): 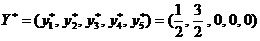. Следовательно, оптимальное значение 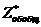, равное по первой теореме двойственности 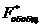, имеет вид

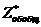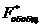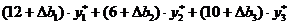= = (7.6)

Рассматривая максимальную прибыль 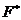в обобщённой задаче (2.1)-(2.2) как функцию доступных объёмов сырья 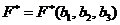, мы приходим в силу (7.6) к формулировке третьей теоремы двойственности:

Теорема.Приращения оптимального значения целевой функции задачи линейного программирования, взятые в отношении к небольшим приращениям правых частей ограничений, равны соответствующим компонентам оптимального решения двойственной задачи; иными словами,

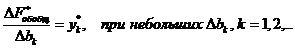
Например, если мы хотим узнать, насколько изменится максимальная прибыль на нашем заводе из задачи (2.1)-(2.2) при увеличении запаса сырья 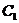на небольшую величину 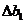, мы находим

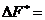
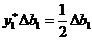. (7.7)

Формулы вида (7.7) «работают» только при небольших 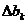. Диапазоны значений 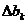, для которого эти формулы применимы, можно явно вычислить. Для этого необходимо заменить в (7.5) базисные переменные последнего шага симплекс-метода их выражения через свободные переменные этого шага, привести подобные члены и записать условия неотрицательности получившихся коэффициентов при свободных переменных (именно в этом случае соответствующее базисное решение (7.2) по-прежнему будет оптимальным и, стало быть, формулы (7.7) будут применимы). Соответствующие вычисления мы предлагаем читателям для самостоятельной работы (или см. [1], стр. 118-120).

Раздел 8

Транспортная задача

Транспортная задача – это задача нахождения оптимального (наименее затратного) плана перевозок. Рассмотрим в качестве примера ситуацию, когда у нас имеется три географически разделённых поставщика некоторого сырья, производящие 60, 10 и 90 единиц сырья в сутки, и удалённые от них четыре фабрики, использующие это сырьё в производстве, суточные потребности которых – 20, 40, 70 и 30 единиц. Пусть имеются некоторые транспортные магистрали, ведущие от каждого поставщика к каждой фабрике, причём затраты 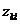на перевозку одной единицы сырья от поставщика с номером k до фабрики номер l по этим магистралям выражаются таблицей:

	№ 1	№ 2	№ 3	№ 4
№ 1
№ 2
№ 3

(8.1)

Составление плана перевозок (плана распределения поставок) означает формирование 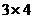матрицы ( 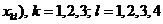; где 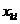− это объём сырья перевозимого ежесуточно от k-го поставщика к l-й фабрике. При этом мы хотим добиться того, чтобы

1) потребности каждой фабрики в сырье были полностью удовлетворены;

2) всё сырье, производимое каждым поставщиком, было реализовано;

3) общие затраты на перевозку сырья были минимальными.

Нахождение такого плана перевозок и составляет содержание транспортной задачи.

Совершенно очевидно, что условия 1 и 2 могут быть выполнены, только если суммарная мощность поставщиков равняется в точности суммарному спросу производителей (предполагаем, что сырье не теряется и не исчезает в ходе его транспортировки). Если это условие равенства выполнено, транспортная задача называется закрытой. В противном случае она называется открытой. Вначале мы будем рассматривать закрытые задачи. Наш конкретный пример является закрытой задачей, т.к. 60+10+90=20+40+70+30=160.

Запишем математически требования 1, 2, 3 для нашего примера:

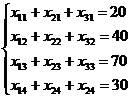
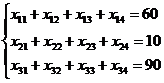(8.2)

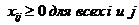
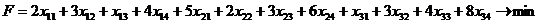
Мы видим, что транспортная задача является задачей линейного программирования, и можно было бы этим замечанием и ограничиться, если бы не тот факт, что непосредственное применение описанной выше техники симплекс-метода в данном случае не очень-то удобно. Для транспортной задачи разработана специальная модификация симплекс-метода, рассмотрением которой мы и займёмся.

Первое, что рекомендуется сделать при решении транспортной задачи с m поставщиками и n потребителями – это проверить её на закрытость. Если она является закрытой, то далее мы вычисляем некоторое важное число: ( 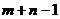). Оно выражает количество базисных переменных в симплекс-методе для нашей транспортной задачи. В нашем примере мы будем иметь 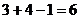базисных переменных (и, стало быть, 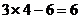свободных).

Следующий этап решения – нахождение первоначального распределения поставок. Существует несколько способов его построения, но мы рассмотрим только метод наименьших затрат. Этот метод удобен тем, что для несложных задач он иногда сразу же выдаёт оптимальное распределение поставок. Модифицируем таблицу (8.1) и условимся помещать объёмы планируемых поставок 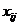в правый нижний угол клетки (i, j).

(8.3)

Выбираем клетку (клетки) с наименьшей ценой перевозки одной единицы сырья:

клетки (1, 3) и (3, 1) в данном случае (клетка (1, 3) означает клетку первой строки третьего столбца). Какую максимальную перевозку можно осуществить в клетке (1, 3)? Первый поставщик может дать максимум 60 единиц, а третья фабрика имеет потребность 70 единиц. Следовательно, максимально возможная перевозка составляет 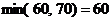единиц. Для клетки (3, 1): третий поставщик может выдать до 90 единиц, но первой фабрике необходимо лишь 20 единиц. Значит, для клетки (3, 1) наибольшая поставка составляет 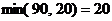единиц сырья. Разумно было бы сразу же побольше «загрузить» наименее затратные линии, поэтому принимаем решение отправлять ежесуточно 60 ед. по маршруту «первый поставщик − третья фабрика»; т.е. ставим 60 в правом нижнем углу клетки (1, 3). После этого перечёркиваем жирной линией эту клетку в знак того, что она стала базисной. Все остальные клетки первой строки будут иметь нулевые поставки (первый поставщик свои мощности уже полностью реализовал) и будут свободными. Мы их перечеркнём прерывистой чертой, но нули ставить явно не будем (как говорится, мы вычеркнем первую строку):

Заметим сразу же, раз и навсегда (внимание!), что если бы в этой ситуации и потребности третьей фабрики были тем самым удовлетворены полностью, то всё же третий столбец «вычёркивать» не надо, т.е. на каждом шаге мы будем «вычёркивать» либо строку, либо столбец!

Теперь в оставшейся части таблицы наименее затратной является клетка (3, 1). Мы ставим туда наибольшую возможную поставку 20 единиц и «вычёркиваем» первый столбец (потребности первой фабрики уже полностью удовлетворены):

Продолжаем аналогично: в оставшейся части таблицы наименее затратная – это клетка (2, 2). Помещаем в неё максимально возможную для неё в данной ситуации поставку 10 ед. и «вычёркиваем» вторую строку:

Теперь мы будем иметь дело с клеткой (3, 2). У третьего поставщика из 90 единиц остались доступными 90-20=70 единиц. А второй фабрике необходимо ещё 40-10=30 единиц. Таким образом, наибольшая возможная поставка в эту клетку будет составлять 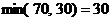единиц сырья.

Рассуждая аналогично относительно двух оставшихся клеток, приходим к первоначальному распределению поставок:

(8.4)

Обратите внимание, что «жирно» перечёркнутых (т.е. базисных) – ровно 6 клеток,

как и должно быть. Общие затраты на перевозку при таком плане составят

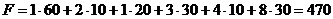денежных единиц.

Но нельзя ли добиться лучшего?

Для выяснения того, является ли данный план перевозок оптимальным, применяют так называемый метод потенциалов. Опишем его. Отметим в таблице затрат (8.1) клетки, соответствующие базисным. И вновь нам предстоит некоторая (несложная на этот раз) игра. Мы будем изменять числа в этой таблице таким образом, чтобы добиться всех нулей в отмеченных клетках. Разрешается при этом прибавлять одно и то же число ко всем элементам строки или столбца. (Эти числа и называются потенциалами строки или столбца.) Утверждается, что требуемой цели всегда можно добиться: в клетках, соответствующих базисным, будут стоять нули. При этом можно доказать, что в остальных клетках, соответствующих свободным, будут стоять коэффициенты при соответствующих свободных переменных в выражении целевой функции через них. Таким образом, план перевозок будет оптимальным тогда и только тогда, когда в конце рассматриваемой игры мы не увидим в таблице никаких отрицательных чисел (это следует из общего критерия оптимальности для задач линейного программирования).

Если же в таблице будет некоторое отрицательное значение, то это значит, что, размещая вместо нулевой некоторую положительную поставку в этой клетке, мы добьёмся экономии общих затрат. Вернёмся к примеру.

Мы рекомендуем вначале отметить те из выделенных клеток, которые «в одиночестве» стоят либо в строке, либо в столбце. С ними нет проблем: их можно «занулить» в любой момент. Займёмся более «трудными» клетками (в примере – клетки (3, 2) и (3, 3)). Чтобы получить в них нули, прибавим ко всем элементам второго столбца (-3), а ко всем элементам третьего столбца – (-4). Получим

		-3
	-1	-1

А теперь без труда справляемся с остальными:

		-3	-4
	-1	-1	-2

			-1
			-1

Игра окончена, и мы видим, что наше распределение поставок не является оптимальным. В силу последней таблицы мы можем написать выражение для целевой функции:

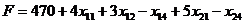, (8.5)

из которого видно, что на каждую дополнительную единицу поставок в клетку (1, 4) (или в клетку (2, 4)) мы получаем экономию в одну денежную единицу. Выбираем одну из них, например, клетку (1, 4), и постараемся поместить в неё наибольшую возможную поставку. Как её вычислить? Это делается путём построения так называемых циклов пересчёта. Пусть в клетке (1, 4) помещена поставка z единиц вместо нулевой. В таблице поставок (8.4) мы имели «бухгалтерский» баланс, т.е. сумма поставок по строкам равна мощностям поставщиков, а сумма поставок по столбцам равна потребностям фабрик. Поместив z единиц в клетку (1, 4), мы нарушили баланс и теперь надо его восстановить только за счёт изменения поставок в базисных клетках. Для первой строки единственным вариантом является поставка 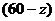в базисной клетке (1, 3). Теперь нарушился баланс в третьем столбце и для его восстановления есть один выход: увеличить на z поставкув клетку (3, 3). Наконец, для восстановления баланса в третьей строке помещаем 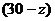единиц в клетку (3, 4); чем замыкается цикл пересчёта, т.к. и в последнем столбце баланс восстановился. Удобно обозначать цикл пересчёта лишь знаками «+» и « −» (соответственно, прибавление z к поставке или вычитание z из неё).

Замечание. Разумеется, в более сложных примерах и циклы пересчёта могут оказаться более сложными – могут представлять собой более сложные замкнутые ломаные. При этом их нахождение может быть своего рода игрой «в лабиринт», если на некоторых шагах имеется более одного варианта восстановления баланса. Тогда нам необходимо выбирать, по какому «туннелю» пойти дальше: ведь при неверном выборе мы попадём в «тупик» − нарушим баланс в строке или столбце без возможности восстановления. Таким образом, придётся просчитывать заранее дальнейшие «пути». И всё же можно доказать, что выход из «лабиринта» всегда может быть найден – мы всегда сможем «замкнуть» цикл пересчёта и вернуться в исходную клетку, полностью восстановив, тем самым, баланс в таблице.

Вернёмся к нашему примеру:

			1 −	4 +   z
			4 +	8 −

Какое же наибольшее z мы можем здесь взять? Очевидно, что ограничения возникают лишь в клетках цикла со знаком «−», и в нашем примере 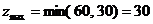. Пересчитывая поставки с этим конкретным значением z, получаем новое распределение поставок (на 30 денежных единиц более экономное в силу формулы (8.5)):

(8.6)

Обратите внимание, что клетка (1, 3), получив 30 единиц, стала базисной; а клетка (3, 4), в которой поставка стала нулевой, превратилась в свободную (обычная «замена игроков» симплекс-метода). При этом количество базисных клеток по-прежнему осталось равным 6.

Замечания.

1. Если при пересчёте по циклу в двух или более клетках образовались нули, то только одну из них (любую) мы превращаем в свободную. Остальные остаются базисными с нулевыми поставками. Это необходимо для сохранения количества базисных клеток.
2. Может случиться, что 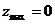. Действуем тогда аналогично, просто пересчитывая нулевую поставку по циклу. При этом начальная клетка (с поставкой z) становится базисной с нулевой поставкой, а какая-то из клеток цикла – свободной.

Теперь мы должны выяснить, является ли план поставок таблицы (8.6) оптимальным. Это делается методом потенциалов, описанным выше. Мы исходим из таблицы затрат на перевозку, в которой отметим новые базисные клетки:

Теперь прибавляем к строкам или столбцам некоторые потенциалы, чтобы добиться нулей в отмеченных клетках (как описано выше). В конце концов, мы приходим к таблице:

Мы видим, что таблице отсутствуют отрицательные числа; значит, распределение из таблицы (8.6) обеспечивает абсолютный минимум транспортных затрат: 470−30=440 денежных единиц. Задача решена.

Конечно же, в других подобных задачах количество шагов до достижения оптимального распределения может быть больше.

Рассмотрим, наконец, вкратце открытые транспортные задачи. Пусть имеется три потребителя сырья с суточными потребностями в 20, 50 и 30 единиц (суммарная потребность – 100 ед.) и три поставщика с ежесуточными мощностями производства 40, 25 и 15 единиц (суммарная мощность производителей – 80 ед.). При этом стоимости доставки одной единицы сырья по различным маршрутам выражается таблицей:

	№ 1	№ 2	№ 3
№ 1
№ 2
№ 3

Возникает, как и раньше, задача нахождения наименее затратного плана перевозок. Однако в данном примере невозможно удовлетворить всем условиям 1,2,3 из начала раздела, т.к. суммарная суточная мощность поставщиков меньше общей потребности потребителей. Задача оказывается открытой. Метод её решения состоит в введении фиктивного поставщика, который компенсировал бы дефицит поставок: в данном случае, в ежесуточном объёме 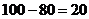единиц сырья. Что же нам взять в качестве транспортных издержек на перевозку одной единицы сырья от этого фиктивного поставщика к нашим потребителям; например, к первой фабрике? Рассуждаем так: одна единица сырья, «поставленная» от фиктивного производителя на первую фабрику … её там на самом деле не будет, т.к. производитель – фиктивный! Следовательно, фабрика потерпит определённый убыток из-за нехватки сырья для производства. Вот этот убыток и следует считать «транспортной издержкой» при «перевозке» одной единицы сырья от фиктивного поставщика на первую фабрику. Аналогично и для остальных потребителей. Итак, если для каждой фабрики данные величины (убытки) известны, мы помещаем их в клетки последней строки таблицы, в левый верхний угол, в качестве транспортных издержек. А если данная информация неизвестна, то считаем данные убытки одинаковыми для всех фабрик и ставим в соответствующие клетки одинаковое число, которое (как можно показать из метода потенциалов) можно считать нулём. Итак, приходим к новой закрытой транспортной задаче:

Далее мы решаем эту закрытую задачу методом, описанным выше, и находим оптимальный план перевозок. Естественно, что при этом объёмы «перевозок» в последней строке будут обозначать объёмы дефицита сырья на соответствующих фабриках (если они равны нулю, значит, потребности соответствующих фабрик будут удовлетворены полностью).

Если, наконец, открытость транспортной задачи обусловлена тем, что суммарная мощность поставщиков больше общего спроса потребителей (перепроизводство!), то мы вводим фиктивного потребителя и соответствующие транспортные издержки на перевозку одной единицы сырья от поставщика к несуществующему потребителю следует положить равными, например, суточным затратам производителя на хранение этой единицы сырья на своих складах. (Если эти данные известны; а иначе, как и выше, положить их все нулями.)

Раздел 9