Обработка и анализ результатов моделирования систем

Общие положения

Для обработки данных эксперимента существуют различные методы, зависящие от целей исследования и вида получаемых при моделировании характеристик.

В результате эксперимента получают набор данных, между которыми может существовать или отсутствовать функциональ­ная либо структурная связь. Если такая связь между факторами и откликом существует, то она проявляется в эксперименте в не­явном виде, а для использования результатов эксперимента в практических целях неявную зависимость следует сделать явной и представить ее в виде функции, системы уравнений, номограм­мы, графика и т. п. Если функциональная зависимость между факторами и откликом не существует, то следует обработать их независимо друг от друга по правилам математической статисти­ки.

Первым шагом при записи аналитического выражения, ап­проксимирующего требуемую зависимость, является нанесение экспериментальных точек на график в прямоугольной системе координат. В результате будет получена диаграмма разброса (рис.1.22), из которой часто удается визуально найти плавную кривую и определить соответствующую ей функциональную зависи­мость. Точки, изображенные на рис.1.22, а, группируются около прямой, а точки, показанные на схеме б, соответствуют кривой. Описание точек схемы в зависит от задач эксперимента: это может быть прямая линия или некоторая периодическая функ­ция. При построении диаграммы разброса нужно иметь в виду постоянно возникающую трудность графического изображения соотношений, связывающих большое число переменных. Частич­но эту трудность можно преодолеть, построив несколько графи­ков, каждый из которых отражает зависимость функции отклика от одной переменной при фиксированных значениях всех оста­льных.

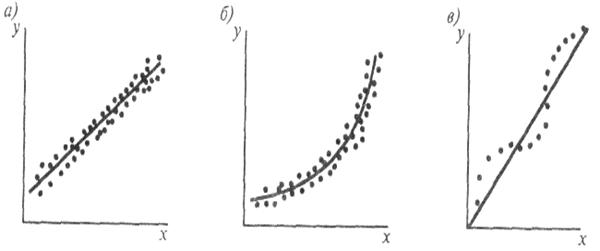Рис. 1.22. Диаграммы разброса

Задачу подбора вида функции, наилучшим образом соответст­вующей конфигурации кривой, называют подгонкой кривых по точкам. Для этой цели используют графические изображения наиболее характерных функций, некоторые из которых показаны на рис. 1.23.

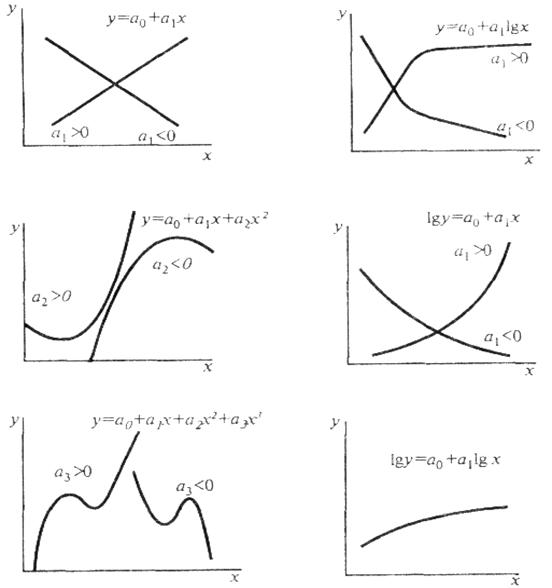
Рис. 1.23. Различные виды регрессионных кривых

При подгонке кривых по точкам, прежде всего, следует опреде­лить количественный принцип соответствия теоретической функ­ции экспериментальным точкам. В качестве меры такого соответ­ствия было бы логичным принять минимальные отклонения по всем точкам, т. е. суммы всех отклонений. Но поскольку отклонения теоретических значений от экспериментальных могут быть положительными и отрицательными, то с математической точки зрения проще предварительно возвести эти отклонения в квадрат и обеспечить минимум для суммы квадратов отклонений. Этот метод, названный методом наименьших квадратов, соответствует критерию наилучшего приближения.

Для поиска математических зависимостей между переменны­ми по накопленным экспериментальным данным обычно исполь­зуют методы регрессионного и корреляционного анализов. Ре­грессионный анализ дает возможность построить по эксперимен­тальным данным уравнение, а корреляционный анализ позволяет судить, насколько хорошо экспериментальные точки согласуются с выбранным уравнением, а также насколько тесна связь между двумя и более величинами, наблюдаемыми и фиксируемыми при моделировании.

Регрессионный анализ. Математический метод, обеспечива­ющий такую подгонку выбранной кривой, при которой она в смысле критерия наименьших квадратов наилучшим образом описывает экспериментальные точки называют регрессионным анализом.

Корреляционный анализ.Наилучшее приближение теоре­тической кривой к экспериментальным данным еще не означа­ет, что реально существующая физическая зависимость соответ­ствует именно этой кривой. Наглядный этому пример дает рис.1.22,в. Описание экспериментальных точек прямой линией впол­не соответствует методу наименьших квадратов, но не соот­ветствует физической сущности явления, если мы не постулируем приближенное представление последнего в линейной поста­новке.

Для оценки согласованности экспериментальных точек с те­оретическими прогнозами используют понятие корреляции. Если регрессия определяет эту согласованность по форме, то кор­реляция показывает, насколько точно она отражает действитель­ность. Вместе с тем корреляция между переменными означает лишь то, что их изменения взаимосвязаны, однако это еще не доказывает наличие причинно-следственной связи между пере­менными.

Мерой корреляционной связи между переменными X и Y слу­жит коэффициент корреляции r_xy, представляющий собой отно­шение корреляционного момента (математического ожидания произведения отклонений X и Y) к произведению средних квадратических отклонений этих величин r_ху = μ_ху /(σ_хσ_у).

Для случая простой линейной регрессионной задачи (т. е. для случая, когда имеются одна зависимая и одна независимая переменные, связанные между собой линейно) коэффициент корреля­ции вычисляют по формуле

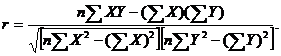(1.84)

Коэффициент корреляции лежит в пределах от -1 до +1. Коэффициент корреляции, равный нулю, соответствует полному отсутствию корреляции (рис.1.24, а). При наличии слабой (схема б) или сильной (схема в) положительной корреляции коэффици­ент корреляции соответственно равен +1 или близок к нему. Если этот коэффициент равен - 1, то имеет место сильная от­рицательная корреляция (схема г).

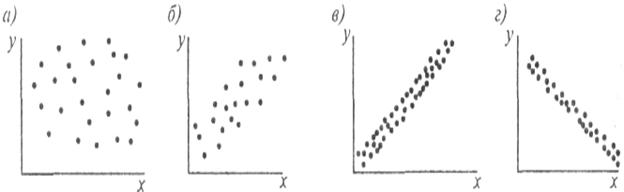
Рис. 1.24. Виды корреляции

Метод наименьших квадратов

Рассмотрим особенности регрессионного анализа результатов моделирования на примере построения линейной регрессионной модели [16], [24].

Основы метода

На рис.1.24 показаны точки (x_i, у_i), полученные в эксперименте. Делаем предположение, что функция отклика может быть пред­ставлена в виде прямой линии

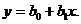(1.85)

Требуется получить такие значения коэффициентов b₀ и b₁, при которых сумма квадратов ошибок будет минимальной. На ри­сунке ошибки e_t для каждой экспериментальной точки равны расстояниям по вертикали от этой точки до линии регрессии (1.85).

Обозначим (y_t)_i=b₀ + b₁ x_i (здесь (у_t)_i — величина, предсказыва­емая регрессионной моделью), тогда выражение для ошибок будет иметь вид

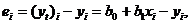а функция ошибки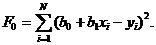

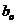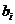Для получения коэффициентов и , при которых функция F₀ будет минимальной, приравняем нулю част­ные производные 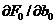и 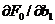. Бу­дем иметь:

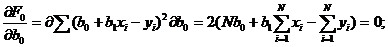
(1.86)

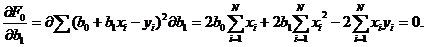
Таким образом, получена система двух линейных алгебра­ических уравнений:

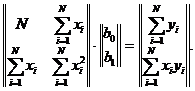(1.87)

Решая систему этих уравнений, получим

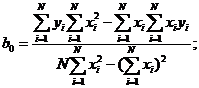
(1.88)

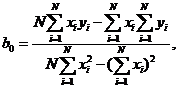
где N - число реализаций при моделировании.

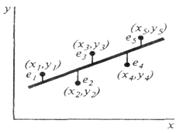
Рис.1.25. К построению рег­рессионной модели

Мы рассмотрели частный случай для уравнения (1.85). В более общем случае, когда эмпирическую функцию принимают в виде полинома

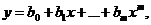(1.89)

система уравнений типа (1.86), (1.87) будет иметь вид

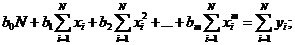
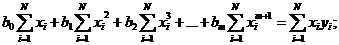(1.90)

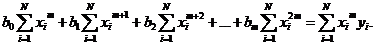
Для оценки точности совпадения теоретических и эксперимен­тальных данных следует определить среднюю квадратичную ошибку на единицу веса

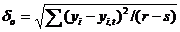(1.91)

или среднее абсолютное отклонение

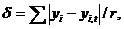(1.92)

где r - число вычисляемых (табличных) значений; s - число параметров.