Фиктивные переменные в уравнении регрессии

Фикт пер-сконструированные переменные (качественные переменные преобразованные в количественные)

Фиктивная переменная — это индикаторная переменная, отражающая качественную характеристику. Чаще всего применяются бинарные фиктивные переменные, принимающие два значения, 0 и 1, в зависимости от определенного условия. Например, в результате опроса группы людей 1 может означать, что опрашиваемый — мужчина, а 0 — женщина. К фиктивным переменным иногда относят регрессор, состоящий из одних единиц (т.е. константу, свободный член), а также временной тренд. Фиктивные переменные, будучи экзогенными, не создают каких-либо трудностей при применении ОМНК. Фиктивные переменные являются эффективным инструментом построения регрессионных моделей и проверки гипотез.

В общем случае, когда качественный признак имеет более двух значений, вводится несколько бинарных переменных. При использовании нескольких бинарных переменных необходимо исключить линейную зависимость между переменными, так как в противном случае, при оценке параметров, это приведет к совершенной мультиколлинеарности. Поэтому применяется следующее правило: если качественная переменная имеет k альтернативных значений, то при моделировании используются только k -1 фиктивная переменная. В регрессионных моделях применяются фиктивные переменные двух типов: переменные сдвига и переменные наклона.

Фиктивные переменные сдвига. Пример

Фиктивная переменная — качественная переменная, принимающая значения 0 и 1, включаемая в эконометрическую модель для учёта влияния качественных признаков и событий на объясняемую переменную. Фиктивная переменная сдвига - это переменная, которая меняет точку пересечения линии регрессии с осью ординат в случае применения качественной переменной.

Фиктивная переменная сдвига. Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых лиц уравнение регрессии имеет вид: 𝒚= 𝒃𝟎+𝒃𝟏∗𝒙+𝜺, где y - количество потребляемого кофе; x - цена. Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола: 𝑦1=𝑏0+𝑏11∗𝑥1+𝜀1 и женского - 𝑦2=𝑏0+𝑏12∗𝑥2+𝜀2. Различия в потреблении кофе проявятся в различии средних 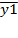и .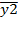

Вместе с тем сила влияния x на y может быть одинаковой, т.е. 𝑏1≈𝑏11≈𝑏12. В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения у1 и у2 и, вводя фиктивные переменные, можно прийти к следующему выражению: 𝑦=𝑎1∙𝑧1+𝑎2∙𝑧2+𝑏1∙𝑥+𝜀, (8.2) где 𝑧1 и 𝑧2 - фиктивные переменные, принимающие значения:

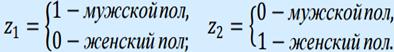
В общем уравнении регрессии зависимая переменная у рассматривается не только как функция цены 𝑥, но и пола (𝑧1;𝑧2). Переменная z рассматривается как двоичная переменная, принимающая всего два значения: 1 и 0. При этом когда 𝑧1 = 1, то 𝑧2 = 0, и наоборот. Для лиц мужского пола, когда 𝑧1 = 1 и 𝑧2 = 0, объединенное уравнение регрессии составит: у = а1 + 𝑏1∙𝑥, а для лиц женского пола, когда 𝑧1 = 0 и 𝑧2 = 1 уравнение регрессии у = а2 + 𝑏1∙𝑥. Иными словами, различия в потреблении кофе для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: 𝑎1≠𝑎2. Параметр 𝑏1 является общим для всей совокупности лиц, как для мужчин, так и для женщин.

Однако при введении двух фиктивных переменных 𝑧1 и 𝑧2 в модель у = а1∙𝑧1 + а2∙𝑧2+𝑏1∙𝑥 +𝜀 (8.4) применение МНК для оценивания параметров а1 и а2 приведет к вырожденной матрице исходных данных, и невозможности получения оценок коэффициентов уравнения регрессии. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т.е. уравнение примет вид у = 𝑏0 + а1∙𝑧1 + а2∙𝑧2+𝑏1∙𝑥 +𝜀.

Предполагая при параметре 𝑏0 независимую переменную, равную 1, имеем следующую матрицу исходных данных (объясняющих переменных):

В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего столбцов. Поэтому матрица исходных факторов вырождена

Выходом из создавшегося затруднения может явиться переход к уравнениям y = 𝒃𝟎+𝑏1𝑥+𝑏2𝑧1+𝜀, или y = 𝒃𝟎+𝑏1𝑥+𝑏2𝑧2+𝜀, т.е. каждое уравнение включает только одну фиктивную переменную 𝑧1 или 𝑧2.

Предположим, что определено уравнение 𝑦=𝑏0+𝑏1∙𝑥+𝑏2∙𝑧+𝜀, где z принимает значения 1 для мужчин и 0 для женщин. Теоретические значения размера потребления кофе для мужчин будут получены из уравнения 𝑦=𝑏0+𝑏1∙𝑥+𝑏2. Для женщин соответствующие значения получим из уравнения 𝑦=𝑏0+𝑏1∙𝑥. Сопоставляя эти результаты, видим, что различия в уровне потребления мужчин и женщин состоят в различии свободных членов данных уравнений: 𝑏0 - для женщин и 𝑏0+𝑏2 - для мужчин.

Теперь качественный фактор принимает только два состояния, которым соответствуют значения 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Вывод: Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели

Пример. Проанализируем зависимость цены двухкомнатной квартиры от ее полезной площади. При этом в модель могут быть введены фиктивные переменные, отражающие тип дома: «хрущевка», панельный, кирпичный. При использовании трех категорий домов вводятся две фиктивные переменные: z1 и z2. Пусть переменная z1 принимает значение 1 для панельного дома и 0 для всех остальных типов домов; переменная z2 принимает значение 1 для кирпичных домов и 0 для остальных; тогда переменные z1 и z2 принимают значения 0 для домов типа «хрущевки».

Предположим, что уравнение регрессии с фиктивными переменными имеет вид: у = 320 + 500x+2200z1 +1600z2. Частные уравнения регрессии для отдельных типов домов, свидетельствуя о наиболее высоких ценах квартир в панельных домах, будут иметь следующий вид: «хрущевки» - у = 320 + 500x; панельные - у = 2520 + 500x; кирпичные - у = 1920 + 500x. Параметры при фиктивных переменных z1 и z2 представляют собой разность между средним уровнем результативного признака для соответствующей группы и базовой группы. В рассматриваемом примере за базу сравнения цены взяты дома «хрущевки», для которых z1 = z2 = 0

Параметр при z1, равный 2200, означает, что при одной и той же полезной площади квартиры цена ее в панельных домах в среднем на 2200 ден.ед. выше, чем в «хрущевках». Соответственно параметр при z2 показывает, что в кирпичных домах цена выше в среднем на 1600 ден.ед. при неизменной величине полезной площади по сравнению с указанным типом домов.