Анализ мультиколлинеарности в нелинейных моделях

При нелинейной связи между факторами в моделях множественной регрессии, анализ мультиколлинеарности проводится с помощью частных коэффициентов корреляции. Частные коэффициенты корреляции рассчитываются между одним из факторов и результатом, при устранении влияния других факторов, а так же между отдельными факторами при устранении влияния других. Выборочный коэффициент частной корреляции вычисляется по формуле:

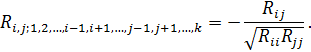
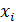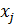Этот коэффициент отражает тесноту связи между и при постоянных значениях других факторов. Здесь 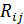– алгебраическое дополнение элемента 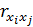корреляционной матрицы R. Очевидно, частный коэффициент корреляции изменяется от -1 до +1. Вычисление коэффициентов частной корреляции используется при отборе факторов в линейную модель регрессии с целью исключения мультиколлинеарности, а так же – целесообразности включения в модель того или иного фактора.

Для двухфакторной модели регрессии 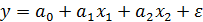частные коэффициенты корреляции между результативным признаком y и одним из факторов 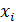при элиминировании его взаимодействия с другим фактором 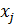даются формулами:

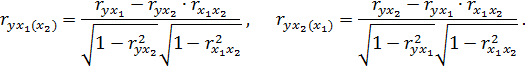
Если окажется, например, что 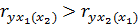, то возможно, что включение в модель фактора 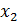нецелесообразно и надо искать другой фактор. Для уравнения регрессии 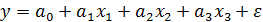возможны уже три коэффициента частной корреляции: 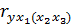, , 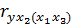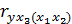. В частности,

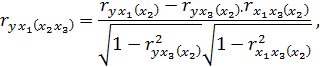
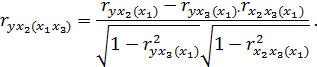
В случае мультиколлинеарности объясняющих факторов, совокупно воздействующих на результативный признак, оценки параметров 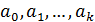полученные по МНК, оказываются особенно чувствительными к незначительным изменениям объема выборки.

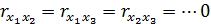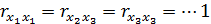О наличии мультиколлинеарности в целом можно судить по величине определителя корреляционной матрицы. В частности, если все факторы линейно независимы, т.е. , а , то

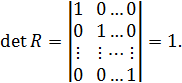
Если между факторами существует полная линейная зависимость, то

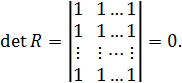
Чем ближе 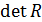к нулю, тем сильнее выражена мультиколлинеарность факторов модели и тем ненадежнее результаты регрессии. Матрица с таким определителем плохо обусловлена и дает большие погрешности при определении силы раздельного влияния факторов на результат. Более детальный анализ мультиколлинеарности позволяют сделать коэффициенты множественной и частной корреляции.

Замечание. Коэффициенты множественной корреляции не сравниваются и самостоятельного экономического смысла не имеют, они в основном используются на стадии формирования модели.

Вопросы для обсуждения

1. Почему необходимо часто строить модель множественной регрессии; приведите примеры экономических процессов и явлений, в которых Вы бы применяли данную модель?

2. В чем отличие целей построения модели парной регрессии и модели множественной регрессии?

3. В чем Вы идите особенность спецификации модели множественной регрессии?

4. Каким требованиям должны отвечать факторы модели множественной регрессии и почему?

5. Как должны соотноситься коэффициенты детерминации для k и k+1 факторов модели?

6. Объясните практическое применение в экономике частных коэффициентов эластичности. Как они вычисляются?

7. В чем заключается смысл расчета скорректированного индекса корреляции и какова связь его с индексом корреляции при различных количествах вводимых в модель факторах?

8. Что при проверке статистических гипотез называют уровнем значимости?

9. Как проверяется значимость уравнения регрессии?

10. Как проверяется значимость коэффициентов уравнения регрессии: в однофакторной и многофакторной моделях?

11. Как вычисляется коэффициент детерминации?

12. Как вычисляются частные коэффициенты корреляции?

13. Что понимается под гомоскедастичностью остатков?

14. Как проверяется гипотеза о гомоскедастичности ряда остатков?

Динамические ряды

Динамическим рядом называется упорядоченная совокупность значений одного экономического показателя (результативного признака) в зависимости от другого (фактора). Например, величина процентной ставки кредитования зависит от процентной ставки рефинансирования, устанавливаемой ЦБ РФ, можно так же рассмотреть зависимость величины приведенной стоимости инвестиций от процентной ставки и др. Если упорядочение экономического показателя проводится по времени, то такой ряд называется временным. Далее термины динамический и временной мы будем употреблять как синонимы.

Примерами динамических рядов являются: показатели заработной платы или пенсий за некоторый период времени; показатели валового внутреннего продукта за ряд лет. Такие ряды характеризуются изменением показателя, т.е. являются нестационарными.

Уровнями ряда называются одномоментные значения экономического показателя. Интервальными называются ряды, полученные агрегированием показателя за некоторый интервал времени.

Длиной временного ряда называют отрезок времени от начального до конечного момента наблюдения. Под длиной временного ряда понимают так же количество входящих в него уровней.

При исследовании динамических рядов различают: 1) задачу анализа уровней временных рядов 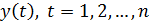и 2) задачу прогнозирования значений экономического показателя в будущем 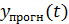для 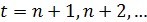Обычно оптимальный горизонт прогнозирования не должен превышать 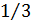объема данных.

Первая задача решается методом покомпонентного анализа с выявлением внутренних связей уровней ряда со временем без установления причин, вторая задача решается методом адаптивных моделей.

При анализе временных рядов традиционно различают разные виды динамики, которые вообще говоря, могут комбинироваться. Тем самым задается разложение временного ряда на составляющие. С экономической точки зрения они имеют разное содержание.

Статистически временной ряд принято характеризовать четырьмя структурными составляющими:

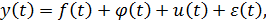где

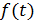– тренд, долговременная составляющая устойчивого изменения экономического показателя, которая выражается аналитической функцией;

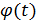– сезонная компонента, характеризует колебания показателя в течение одного года;

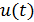– циклическая конъюнктурная компонента, характеризует колебания за период более одного года; 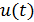– рассматривается в специальных исследованиях.

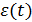– остаточная компонента или случайная составляющая ряда, отражает воздействие многочисленных случайных факторов.

Аддитивная форма ряда более предпочтительна, если значения сезонной компоненты предполагаются постоянными для различных периодов.

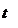
Пример. Пусть аддитивная модель формируется под воздействием трех факторов 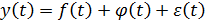. Требуется определить какие данные соответствуют условиям моделирования: а) 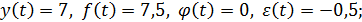б) .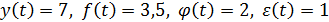

Ответ. Поскольку условиям аддитивного моделирования соответствуют требования суммирования факторов, определяющих результативный признак, то требованиям модели будет удовлетворять набор а): 7=7,5+0-0,5. Набор б) этим требованиям не удовлетворяет: .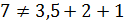

Построение модели динамического ряда включает:

1) предварительный анализ, устраняющий аномальные значения, и выравнивание исходного ряда методом скользящей средней; 2) расчет сезонной компоненты; 3) расчет циклической компоненты (если она присутствует); 4) расчет абсолютных и относительных ошибок.

Динамический ряд может представляться так же в мультипликативной форме:

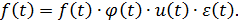
Использование мультипликативной модели целесообразно, если амплитуда колебаний от периода к периоду непостоянна, например, возрастает или уменьшается.

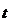
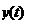
Пример. Пусть мультипликативная модель формируется под воздействием трех факторов 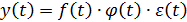. Требуется определить какие данные соответствуют условиям моделирования:

а)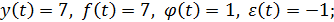

б) ;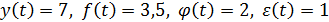

в) .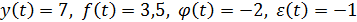

Ответ. Поскольку условиям мультипликативного моделирования соответствуют требования произведения факторов, определяющих результативный признак, то требованиям модели будут удовлетворять наборы б) и в), для которых: 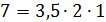и 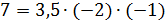. Набор а) этим требованиям не удовлетворяет: .

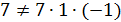Временной ряд называется стационарным, если его свойства с вероятностной точки зрения не зависят от времени. Если эти свойства со временем изменяются, ряд называется нестационарным.

В практической работе стационарные ряды характеризуются отсутствием: тренда; систематических изменений дисперсии экономического показателя; взаимосвязи между уровнями ряда, периодических изменений. Стационарный ряд характеризуется как ряд с показателями: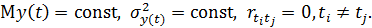

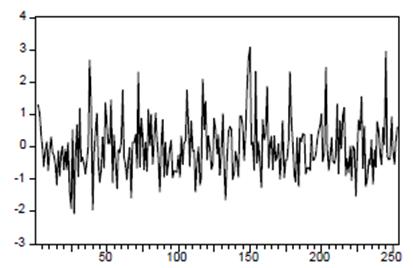
Белым шумом называется случайный процесс, характеризующийся рядом независимых одинаково распределенных случайных величин. Процесс - белый шум некоррелирован по времени, не определяет его значений: в конкретные моменты они могут быть произвольными с точностью до главного статистического свойства (однако постоянная составляющая такого процесса должна быть равна нулю).

В генераторах случайных чисел белый шум используется для генерирования случайных чисел и последовательностей.

Пример стационарного процесса – белый шум изображен на рисунке.