Оценка тесноты связи в многофакторной модели

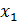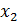Оценки тесноты связи между факторами рассмотрим на примере линейнойдвухфакторной модели. Они определяются как коэффициенты парной корреляции результативной переменной yс каждым из факторов и , а так же факторов между собой:

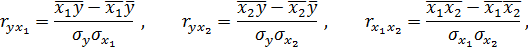
где 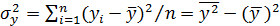– общая дисперсия признака y.

Через вычисленные коэффициенты парной корреляции выражается совокупный коэффициент, или по-другому, коэффициент множественной корреляции:

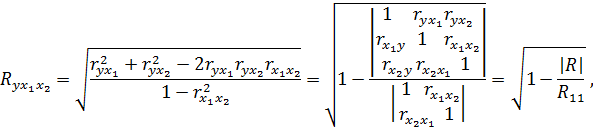
где 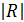– определитель расширенной корреляционной матрицы, 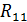– определитель матрицы межфакторной корреляции. Об этом еще будет сказано. Коэффициент корреляции 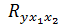обладает свойствами: .

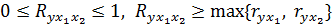Чем ближе 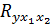к 1-це тем в большей степени учтены факторы, влияющие на результативный признак. Коэффициент 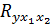характеризует степень совокупного воздействия факторов на экономический результат. Другое представление коэффициента множественной корреляции дается формулой:

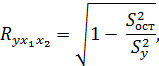
где 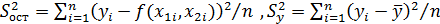– остаточная и общая дисперсия, соответственно.

Теснота связи одного из k факторов модели с остальными 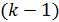дается выборочным коэффициентом множественной корреляции:

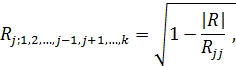
где 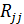– алгебраическое дополнение элемента 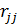корреляционной матрицы R. При обнаружении мультиколлинеарности обычно исключают фактор, наиболее зависимый от комплекса остальных. При этом следует помнить о сохранении экономического смысла факторов. Величина 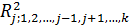определяет долю случайного разброса фактора .

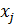Значимость одного и того же фактора в многофакторной модели будет зависеть от последовательности введения его в модель и общего количества факторов модели, в силу имеющейся, практически всегда, корреляции между отдельными факторами. Это обстоятельство затрудняет определение значимости коэффициентов множественной корреляции. Для определения целесообразности включения нового фактора в модель служит частный F-критерий, т.е. 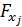. Предположим, что требуется оценить значимость влияния вновь вводимого в модель фактора 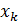на результативный признак y. Формула, по которой оценивается значимость влияния вновь вводимого фактора, имеет вид:

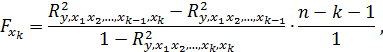
где 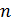– число наблюдений, 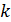– число коэффициентов при факторных переменных (т.е. число параметров модели без свободного члена), 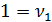– число степеней свободы равное приросту за счет включения в модель одного дополнительного фактора, 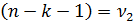– число степеней остаточной суммы квадратов отклонений. Вычисленное значение сравнивается с табличным 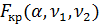и делается заключение о целесообразности включения в модель нового фактора. Если 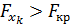, то включение в модель фактора 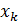статистически оправдано, а коэффициент регрессии 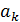при этом факторе признается значимым.

4.3. Оценка качества модели

Качество модели в целом характеризует коэффициент множественной детерминации, который равен квадрату коэффициента (индекса) множественной корреляции 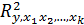. Однако не стоит передоверяться слишком высокому значению 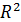, так как величины y и какая-тоx_i могут иметь общий тренд, не связанный с причинно-следственной зависимостью. В большей степени это, впрочем, относится к временным рядам.

Величина коэффициента детерминации приближается к единице при увеличении числа факторов и приближении их количества к – числу степеней свободы общей дисперсии, поскольку остаточная дисперсия в этом случае имеет систематическую ошибку в сторону преуменьшения. При этом, не важно имеют ли вводимые в модель факторы экономический смысл или нет. Чтобы исключить эту неэкономическую погрешность, рассчитывается скорректированный на число степеней свободы, а точнее сказать на их потерю, исправленный коэффициент детерминации:

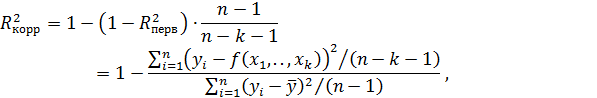
где n – число наблюдений, k – число коэффициентов при переменных x_i, 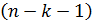– число степеней свободы остаточной дисперсии, 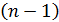– число степеней свободы в целом по совокупности, .

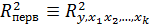Для дисперсионного уравнения множественной регрессии

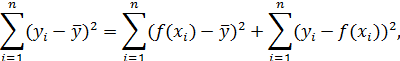
значения дисперсий на одну степень свободы представим таблицей

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Дисперсия на одну степень свободы
Общая		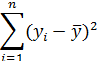n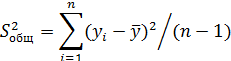
Факторная		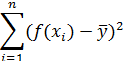k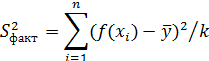
Остаточная		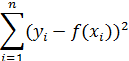n-k-1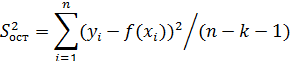

Степени свободы – это количества элементов, которые можно варьировать, не изменяя заданных характеристик.

Значимость модели множественной регрессии в целом оценивается с помощью критерия Фишера:

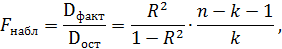
где 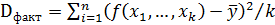– факторная дисперсия на одну степень свободы, 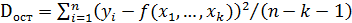– остаточная дисперсия на одну степень свободы, k– число параметров при переменных 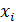(в линейной регрессии совпадает с числом факторов модели). Для парной модели регрессии 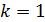, тогда, в частности, будет

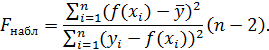
Если вычисленное значение больше табличного, то совокупная связь признаков считается существенной, а коэффициент множественной корреляции – значимым.

В случае двухфакторной модели, общее число параметров 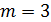и, соответственно, 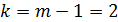, тогда

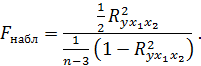
Наблюдаемое значение, сравнивается с табличным 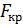при заданном уровне значимости α и числе степеней свободы 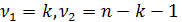, для факторной и случайной дисперсии, соответственно. Если оказывается 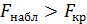, то уравнение в целом признается значимым.

При большом количестве факторов, корреляционно-регрессионный анализ проводится с помощью стандартных статистических программ. Величина 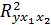показывает долю изменения результативного признака, обусловленную изменением факторов 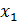и 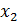, включенных в модель.