Оценка тесноты связи и качества нелинейной модели

При нелинейной зависимости между фактором xи результатом y, для оценки тесноты связи используется корреляционное отношение, или по-другому, индекс корреляции. Исходя из общего соотношения

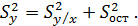
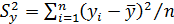– общая дисперсия для совокупности из n наблюдений, учитывающая действие всех факторов нелинейной модели, а именно: фактора x и тех, которые моделью не учтены.

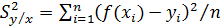– дисперсия, возникающая в результате вариации только фактора x.

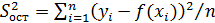– остаточная дисперсия, отражающая вариацию результативного показателя за счет всех остальных, кроме x, факторов, не учтенных в модели нелинейной регрессии.

Индекс корреляции

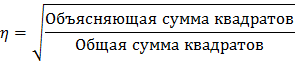
применим ко всем случаям корреляционной зависимости безотносительно к форме этой связи (линейной, нелинейной, многофакторной). В этом смысле он является универсальным показателем тесноты связи. Исходя из общего дисперсионного соотношения, можем написать

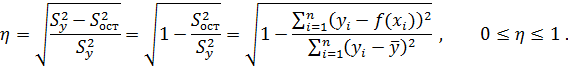
Величина 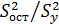– характеризует долю остаточной дисперсии.

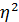Качество модели, ее адекватность, тем выше, чем ближе к 1-це. Квадрат индекса корреляции имеет тот же смысл, что и коэффициент детерминации 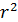. Он оценивает близость линии регрессии к фактическим данным. Выраженный в процентах, квадрат индекса корреляции показывает: насколько процентов общая вариация экономического результата y зависит от объясняющего фактора x.

Для проверки значимости (адекватности) уравнения нелинейной регрессии в целом используется F-критерий Фишера, который представляет собой отношение оценок факторной и остаточной дисперсий, рассчитанных на одну степень свободы. Пусть n – число наблюдений; m – число параметров в уравнении регрессии (оно на 1-цу больше чем число независимых переменных модели); 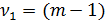– число степеней свободы для факторной дисперсии; 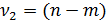– число степеней свободы для остаточной дисперсии.

При такой трактовке входящих параметров, критерий Фишера дается формулой

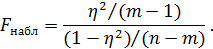
Часто вместо m вводится число коэффициентов регрессии k (в многофакторной модели – это число коэффициентов при переменных 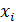), которое на 1-цу меньше числа параметров в уравнении регрессии. Например, в представлении 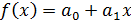есть 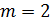параметра 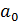и 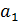, но только один коэффициент регрессии 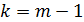. При такой трактовке формула для критерия принимает вид

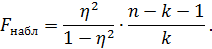
Примеры.

а) , тогда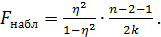

б) 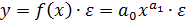, в уравнении регрессии есть два параметра 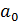и 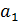, т.е. 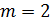и, следовательно, 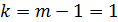. Формула для критерия Фишера 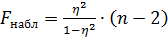, т.е. имеет вид такой же, как при линейной зависимости.

Вычисленное значение 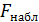сравнивается с табличным 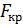для числа степеней свободы 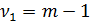и 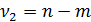и заданного уровня значимости α. Если 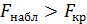, то уравнение признается значимым.

Замечание. Чем больше кривизна линии регрессии, тем более отличается индекс 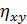от 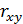, а именно 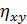растет по отношению к .

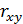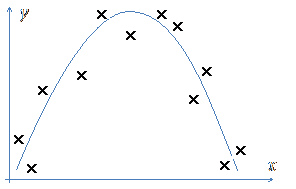Пример. Рассмотрим процесс, в котором результативная переменная y под влиянием фактора xсначала растет с положительным ускорением, а затем с таким же по величине, но отрицательным ускорением замедляется. Точки корреляционного облака статистических данных очевидно можно представить полиномом второй степени – параболой с ветвями, направленными вниз, см. рис. Подобная зависимость хорошо описывает рост урожайности зерновых от количества выпавших осадков. Пусть 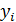– урожайность 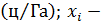осадки (см). Визуально определяем, что корреляционное облако можно аппроксимировать параболой 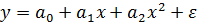. Для нахождения неизвестных коэффициентов 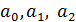можно непосредственно, т.е. без всяких ограничений, использовать метод наименьших квадратов. Представим только общую схему метода:

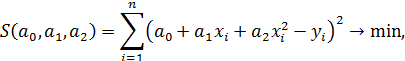
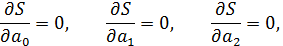
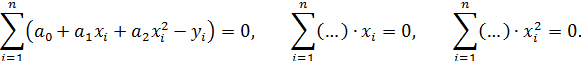
Можно показать, что определитель этой системы отличен от нуля. Тогда решение системы существует, оно единственно и позволяет найти коэффициенты параболы 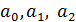.