Нелинейныеоднофакторные модели регрессии

По типу функциональной зависимости факторных и результативных признаков различают линейные и нелинейные модели регрессии. Если зависимость случайной величины от факторного признака носит явно нелинейный характер, то использование линейных моделей может давать большие погрешности. В таких случаях выбор функции требует предварительных исследований. Нелинейными являются процессы динамики социальных и большей частью экономических явлений.

Пример.Пусть fхарактеризует динамику уровня образования населения за последние tлет. Уровень образования –количество людей с высшим образованием на 1000 жителей региона в возрасте лет. Тогда для одного из регионов России была получена функция Гомперца:

.

Пример. Эмпирически установлено, что кривая Гомперца , где c – асимптота функции, хорошо описывает динамику роста уровня жизни, численности населения.

Пример.Процесс изменения спроса на непродовольственные товары в зависимости от доходов семьи хорошо описывается функцией Гомперца . Весь процесс можно разбить на четыре этапа:

1) сначала, с ростом доходов, имеется небольшой рост потребления непродовольственных товаров и, соответственно, небольшой прирост; 2) затем прирост потребления становится весьма существенным; 3) потом начинается замедление прироста; 4) появляется участок-плато и приближение к асимптоте .

Пример. Известно, что кривая Филлипса хорошо описывает зависимостьy–годового темпа прироста заработной платы (в процентах) отx– общего уровня безработицы (в процентах).

Напомним, что прирост означает: .

Для моделирования нелинейных экономических процессов используют функции:

1) – полулогарифмическая;

2) – полиномиальная (при n=2 модель хорошо описывает зависимость спроса от цены, при n=3 хорошо описывает общие издержки в зависимости от объема выпуска продукции, а так же зависимость урожайности от количества внесенных удобрений);

3) – гиперболическая (хорошо описывает зависимость себестоимости y от урожайности x, при выращивании хлопка);

4) – степенная (при модель хорошо описывает трудоемкость в с/х производстве, используется так же при исследовании спроса и потребления);

5) – показательная (находит применение при моделировании процессов с постоянным темпом роста);

6) – обратная;

7) – логистическая;

8) .

Методы линеаризации

Различают модели: а) нелинейные по переменным и линейные по параметрам; б) нелинейные по параметрам. Говорят, что модель внутренне нелинейная, если с помощью элементарных преобразований или замены переменных ее нельзя привести к линейному виду. Таковой является, например, модель 4).

Функции 1)-3) – линейны по оцениваемым параметрам и нелинейны по объясняющим переменным. Остальные функции – нелинейны и по параметрам и по переменным. В случаях 1), 3) и 6) модель можно линеаризовать, положив, соответственно, , и . После этого, для определения коэффициентов, можно воспользоваться МНК. Без формальных ограничений, с помощью МНК, можно определить коэффициенты и для модели 2).

Остальные случаи так же можно исследовать с помощью МНК, если уравнения регрессии должным образом модифицировать.

При после двойного логарифмирования функция Гомперца линеаризуется к виду: . Для нахождения параметров по МНК минимизируем функционал:

.

После проведения всех процедур МНК коэффициенты находим потенцированием, полученных по МНК значений и .

Прологарифмируем уравнение 4), тогда получим

.

Сделаем замены , , , и перепишем исходное уравнение в виде:

Полученное уравнение является линейным относительно новых переменных и для определения его параметров можно воспользоваться МНК. Однако теперь оценка параметров модели будет основываться уже на минимизации суммы квадратов отклонений в логарифмах, т.е.

Пример. Пусть построено уравнение регрессии в логарифмах исходных показателей . Вычисленный коэффициент корреляции между логарифмами исходных показателей составил . Тогда коэффициент детерминации для модели в исходных показателях равен .

Степенная функция 4) получила в экономике большое распространение. Это связано с тем, что параметр 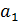имеет ясный экономический смысл – он является коэффициентом эластичности

Ниже приведены зависимости результата y от фактора x, моделирующие процессы с постоянной эластичностью переменной f по переменной x.

Известно, что зависимость объема спроса от цены характеризуется постоянной эластичностью. Поэтому моделирование спроса от цены целесообразно проводить на основе степенной функции, так как из всех нелинейных функций только степенная характеризуется постоянной эластичностью.

Пример. После исследования сети торговых точек было построено уравнение нелинейной регрессии , где f – спрос на продукцию, x – цена продукции. Наблюдаемое (расчетное) значение t-критерия Стьюдента, после линеаризации уравнения регрессии и применения к нему стандартного алгоритма как для уравнения парной регрессии, составило . По таблице были найдены критические значения: , , . Тогда при уровне значимости будет и можно считать эластичность спроса по цене равной . При других уровнях значимости коэффициент 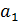– незначим.

Примеры. Приведем коэффициенты эластичности для некоторых других моделей регрессии.

а) – гипербола: ,

б) – показательная: , , , отсюда .

в) – обратная: ,

г) – полулогарифмическая: ,

Прологарифмируем уравнение 5), тогда получим

.

Следуя МНК можно написать систему уравнений:

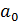Потенцируя найденные из этой системы выражения , , найдем параметры и 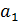исходной модели.

К замене переменных в нелинейных моделях следует относиться с осторожностью и понимать, что минимизация суммы квадратов отклонений для исходных переменных преобразовывается в модифицированную сумму квадратов, что не одно и то же.

Ранее мы уже отмечали, что выбор уравнения регрессии не всегда прост и однозначен, поскольку между одними и теми же признаками x и y зависимость можно выразить разными формулами (уравнениями). Предпочтение следует отдавать тем уравнениям, параметры которых рассчитываются наиболее просто и имеют ясный экономический смысл.