Линейная модель парной регрессии

Рассмотрим зависимость 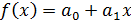. Имеется выборка из nпар значений 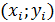. Линейная парная регрессионная модель имеет вид:

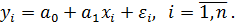
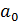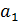Согласно идеологии МНК, требуется найти такие и , которые минимизируют функционал

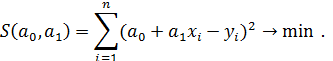
Поскольку 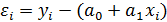, то это условие можно переписать в виде: 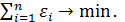Запишем необходимые условия экстремума функционала

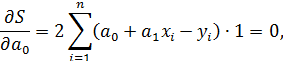
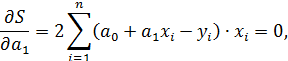
или

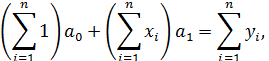
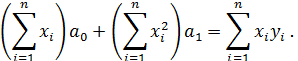
Полученная система, по предположению удовлетворяющая предпосылкам МНК, называется системой нормальных уравнений. Можно показать, что ее определитель отличен от нуля. Она имеет единственное решение и поэтому позволяет однозначно найти параметры регресси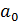и и 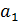. Разделим оба уравнения на количество точек n, тогда получим

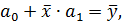
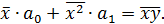
Решаем систему двух линейных уравнений относительно 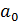и 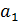. Имеем,

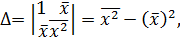
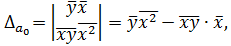
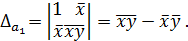
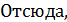
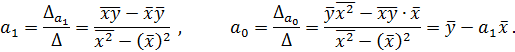
Коэффициент 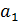называется коэффициентом линейной регрессии. Он имеет экономический смысл и показывает: насколько в среднем изменится результативный признак y при изменении фактора x на 1-цу. Действительно

.

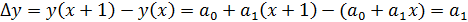Параметр 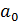экономического смысла не имеет.

Для линейной зависимости легко записать средний коэффициент эластичности:

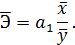
Эластичностьпоказывает насколько процентов, в среднем по совокупности, изменится экономический результат y от своего среднего значения при изменении фактора x на 1% от своего среднего значения. В общем случае коэффициент эластичности Э – переменная величина. Поэтому, если не привязываться к средним значениям экономических факторов x и y, то для линейной зависимости коэффициент эластичности примет вид:

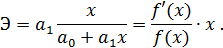
Замечание. Коэффициенту эластичности не всегда можно приписать экономический смысл. Например, бессмысленно измерять изменение в процентах заработной платы при изменении возраста работника на 1%. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения в процентах.

Пример.Требуется построить математическую модель объема продаж yв зависимости от расходов на рекламу x,имея данные распределения двумерной случайной величины 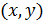. Решение задачи разбивается на 6 этапов и сводится к заполнению таблицы:

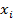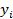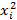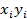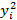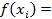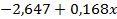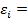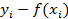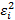№										Пр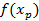
		8,9	43,56	587,4	79,21	8,44	0,46	0,21	0,142
		9,0	47,61		81,0	8,95	0,05	0,003	0,128
		9,3	51,84	669,6	86,49	9,45	-0,15	0,0225	0,092
		9,6	56,25		92,16	9,95	0,05	0,0025	0,058
		10,0	59,29			10,29	-0,29	0,084	0,016
		10,9	67,24	893,8	118,81	11,13	-0,23	0,0529	0,068
		11,6	68,89	962,8	134,56	11,30	0,3	0.09	0,124
		12,0	73,96			11,80	0,2	0.4	0,153
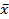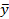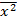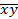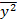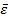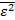									0,978
76,3	10,16	5858,0	782,08	104,53		0,05	0,063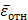

1 этап.Расположение точек на плоскости (нанесите эти точки) дает основание предположить линейную зависимость между xи y. Будем искать .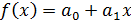

2 этап. Коэффициенты 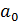и 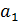находим по методу наименьших квадратов. Для этого сначала вычисляем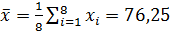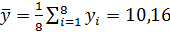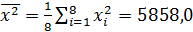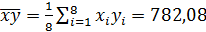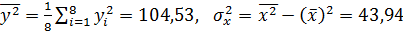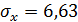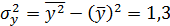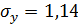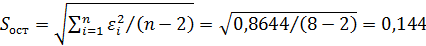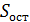: , , , , , , , , . – называется стандартной ошибкой регрессии, 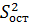– является несмещенной оценкой дисперсии случайных отклонений .

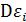Подставим вычисленные значения в формулы для коэффициентов и получим:

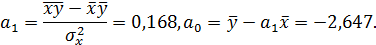
Таким образом, уравнение линейной регрессии имеет вид:

.

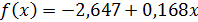3 этап.Вычисляем коэффициент парной корреляции:

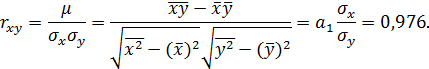
Коэффициент 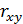, определяющий тесноту связи результативной переменной y и фактора x, стандартизирован. Он выражается в долях среднего квадратического отклонения результативного признака. Отклонение признака-фактора x от его среднего значения на величину своего среднего квадратического отклонения в среднем по совокупности, приводит к отклонению результативного признака y от своего среднего значения на 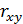его среднего квадратического отклонения.

Поскольку 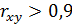, то связь между затратами на рекламу и объемом продаж – весьма высокая.

4 этап.Поскольку 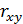, , 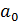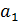определяются по выборочной совокупности и являются лишь оценками статистической закономерности, то необходимо определить значимость коэффициента корреляции и параметров линейной регрессии. Оценим значимость параметров линейной регрессии 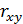, , 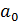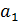и уравнения в целом. Эти оценки в общем итоге зависят от дисперсии результативного признака. Дисперсия всегда имеет место в силу неучета в модели факторов, оказывающих влияние на результативный признак. Оценка значимости линейного коэффициента корреляции базируется на сопоставлении вычисленного значения 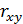с его средней квадратической ошибкой : .

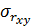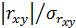Если число элементов выборки велико 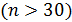, то есть основания полагать, что выборка близка по качеству к генеральной совокупности и, следовательно, все оценки имеют нормальный закон распределения. Тогда средняя квадратическая ошибка коэффициента оказывается несмещенной и может рассчитываться по формуле 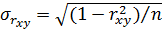, 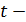критерий можно полагать равным 2. Обычно, при большом n,коэффициент 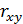превышает среднюю ошибку более чем в три раза, т.е. 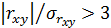. Это всегда означает, что коэффициент корреляции значим, а связь xи yреальна.

Если число элементов выборки невелико 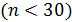, тосредняя квадратическая ошибка коэффициента корреляции является смещенной и рассчитывается по формуле 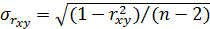. В этом случае значимость коэффициента проверяется с использованием статистики Стьюдента. Об этом еще будет сказано.

Нахождение пригодной линии регрессии для прогноза, а это является нашей главной целью, зависит от того какая часть общей вариации признака yприходится на объясненную вариацию.

В случае парной регрессии коэффициент детерминации совпадает с квадратом коэффициента корреляции 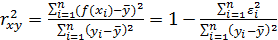. Величина 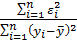определяет долю разброса зависимой переменной, необъясненную регрессией y на x.

Если остаточная сумма квадратов меньше суммы квадратов, обусловленной регрессией, то уравнение статистически значимо и тогда коэффициент детерминации близок к единице. Он показывает, какая доля вариации результативного признакаyнаходится под воздействием фактора x. В нашем случае 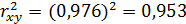. Отсюда заключаем, что вариация результата yболее чем на 95% объясняется вариацией фактора x. На долю прочих факторов, влияющих на результат y, приходится менее 5%. Таким образом, доля остаточной дисперсии в общей дисперсии составляет .

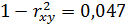Построенная модель достаточно качественно согласует объем продаж с затратами на рекламу.