Некоторые сведения из математической статистики
Вариацией признака называется наличие различий в численных значениях признака внутри однородной совокупности у отдельных элементов. Различают случайную и систематическую вариации.
Генеральной совокупностью называется множество всех теоретически возможных, мыслимых значений (измерений, наблюдений) случайных величин, характеризующих экономический процесс или явление. Характеристики случайной величины, полученные по генеральной совокупности, называются теоретическими.
Выборкой из генеральной совокупности называется ограниченный набор значений случайной величины, характеризующей процесс или явление. Количество этих значений называется объемом выборки. Характеристики случайной величины, полученные по выборке, называются выборочными, или эмпирическими. Выборка из генеральной совокупности должна обладать следующими свойствами: 1) каждый элемент выбирается случайно; 2) все элементы имеют равную вероятность попасть в выборку; 3) объем выборки должен быть репрезентативным и достаточным для решения поставленной задачи с требуемым качеством.
Оценкой 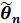 истинной характеристики
истинной характеристики 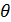 называется случайная величина
называется случайная величина 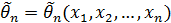 – функция выборочных значений
– функция выборочных значений 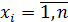 .
.
Несмещенной называется оценка 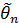 , если ее математическое ожидание равно оцениваемому параметру:
, если ее математическое ожидание равно оцениваемому параметру:
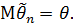
Выполнение этого условия говорит об отсутствии в наблюдениях систематической ошибки. Поскольку в общем случае 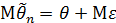 , где
, где 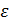 – случайная ошибка (случайный остаток), то несмещенность означает, что
– случайная ошибка (случайный остаток), то несмещенность означает, что 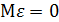 . В математической статистике разность
. В математической статистике разность 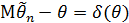 называется смещением оценки
называется смещением оценки 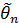 . Дисперсия несмещенной оценки параметра
. Дисперсия несмещенной оценки параметра 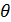 удовлетворяет неравенству Рао-Фреше-Крамера:
удовлетворяет неравенству Рао-Фреше-Крамера:
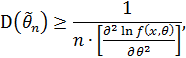
где n – объем выборки, 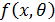 – плотность распределения случайной величины.
– плотность распределения случайной величины.
Состоятельной называется оценка 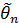 , если при неограниченном увеличении объема выборки, она сходится по вероятности к оцениваемому параметру:
, если при неограниченном увеличении объема выборки, она сходится по вероятности к оцениваемому параметру:
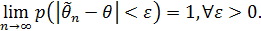
Замечание.В большинстве конкретных случаев несмещенная оценка оказывается и состоятельной.
Эффективной называется оценка, если она имеет минимальную дисперсию в определенном классе оценок, т.е. не существует другой несмещенной оценки с меньшей дисперсией. Границей эффективности является тот средний квадрат отклонения оценки от оцениваемого параметра 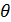 , который уменьшить уже невозможно.
, который уменьшить уже невозможно.
Оценка 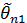 считается эффективнее оценки
считается эффективнее оценки 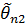 той же характеристики, если для несмещенных оценок
той же характеристики, если для несмещенных оценок 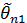 и
и 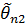 выполняется соотношение:
выполняется соотношение: 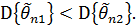 Если оценки
Если оценки 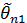 и
и 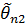 – смещенные, то сравнение эффективности имеет вид:
– смещенные, то сравнение эффективности имеет вид: 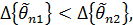 где
где 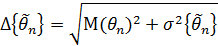 – средний квадрат отклонения оценки. Можно показать, что дисперсия несмещенной оценки не может быть произвольно малой.Мерой эффективности может служить величина:
– средний квадрат отклонения оценки. Можно показать, что дисперсия несмещенной оценки не может быть произвольно малой.Мерой эффективности может служить величина:
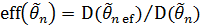 – для несмещенных оценок;
– для несмещенных оценок;
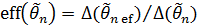 – для смещенных оценок.
– для смещенных оценок.
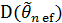 и
и 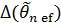 – дисперсия и средний квадрат отклонения, соответственно, более эффективной оценки
– дисперсия и средний квадрат отклонения, соответственно, более эффективной оценки 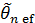 по сравнению с анализируемой оценкой
по сравнению с анализируемой оценкой 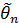 .
.
Примеры. Дисперсией называется средний квадрат отклонений отдельных значений признака от его среднего значения. По-другому, дисперсия – это математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Величина 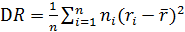 – характеризует рассеяние случайной величины R и называется сгруппированной выборочной дисперсией;
– характеризует рассеяние случайной величины R и называется сгруппированной выборочной дисперсией; 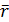 – среднее значение случайной величины R по выборочным данным. Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е.
– среднее значение случайной величины R по выборочным данным. Выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. 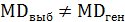 . Поэтому в качестве оценки генеральной дисперсии применяют исправленную дисперсию
. Поэтому в качестве оценки генеральной дисперсии применяют исправленную дисперсию 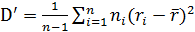 , которая является несмещенной оценкой
, которая является несмещенной оценкой 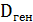 . На практике исправленной дисперсией пользуются, если
. На практике исправленной дисперсией пользуются, если 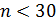 .
.
Величина 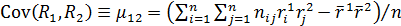 – называется сгруппированной выборочной ковариацией случайных величин
– называется сгруппированной выборочной ковариацией случайных величин 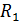 и
и 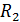 . Здесь
. Здесь 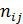 – частота наблюдавшейся пары значений
– частота наблюдавшейся пары значений 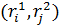 ;
; 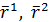 – выборочные средние значения случайных величин
– выборочные средние значения случайных величин 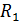 и
и 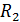 . Ковариация служит для характеристики тесноты связи между случайными величинами. Если
. Ковариация служит для характеристики тесноты связи между случайными величинами. Если 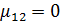 , то
, то 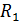 и
и 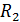 – независимы; если
– независимы; если 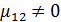 ,
, 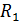 и
и 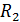 – зависимы.
– зависимы.
Величина 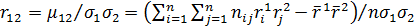 – называется коэффициентом сгруппированной выборочной корреляции случайных величин
– называется коэффициентом сгруппированной выборочной корреляции случайных величин 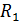 и
и 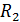 ;
; 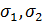 – средние квадратические отклонения
– средние квадратические отклонения 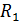 и
и 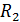 .
.
Смысл 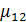 и
и 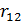 один и тот же. Преимущество коэффициента корреляции перед коэффициентом ковариации состоит в том, что
один и тот же. Преимущество коэффициента корреляции перед коэффициентом ковариации состоит в том, что 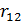 – безразмерная величина. В случае зависимости случайных величин
– безразмерная величина. В случае зависимости случайных величин 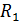 и
и 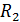 , говорят об уравнении
, говорят об уравнении 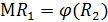 как регрессии
как регрессии 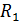 на
на 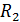 , или
, или 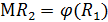 как регрессии
как регрессии 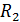 на
на 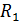 .
.
Пусть 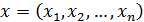 и
и 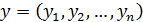 – зависимые случайные величины. Требуется сделать заключение о степени зависимости y и x. Для простоты данные будем считать не сгруппированными. Величина
– зависимые случайные величины. Требуется сделать заключение о степени зависимости y и x. Для простоты данные будем считать не сгруппированными. Величина 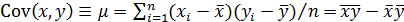 – называется ковариацией совокупности. Величина
– называется ковариацией совокупности. Величина 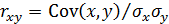 – называется коэффициентом корреляции совокупности. Здесь
– называется коэффициентом корреляции совокупности. Здесь 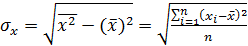 ,
, 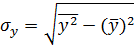 – средние квадратические отклонения случайных величин x и y;
– средние квадратические отклонения случайных величин x и y; 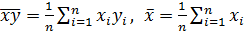 ,
, 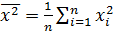 .
.
Располагая только выборочной совокупностью, мы должны понимать, что она сама является случайной величиной. Значит 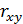 и прочие характеристики, полученные на ее основе, так же будут случайными величинами. Для оценки статистической значимости и построения интервальной оценки, например, выборочного коэффициента корреляции
и прочие характеристики, полученные на ее основе, так же будут случайными величинами. Для оценки статистической значимости и построения интервальной оценки, например, выборочного коэффициента корреляции 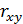 необходимо знать закон распределения оценки
необходимо знать закон распределения оценки 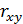 как случайной величины.
как случайной величины.
