Общая характеристика и принципы системного анализа

Анализ сложных процессов и систем должен производится с системный позиций. Термин «системный подход», подчеркивает необходимость исследования объекта с разных сторон, комплексно, в отличие от ранее принятого разделения исследований на физические, химические и др. процессы. Оказалось, что с помощью многоаспектных исследований можно получить более правильные представления о реальных объектах, выявить их новые свойства, лучше определить взаимоотношения объекта с внешней средой, другими объектами.

Системный подход позволяет лучше увидеть существенные стороны объекта исследования, позволяет подняться на новый уровень осмысления системы в целом, выйти за рамки "узкого" отношения к ней. В настоящее время системный анализ является наиболее конструктивным направлением теории систем.

В системном анализе широко используются все базовые категории общей теории систем: элемент, связь, система, большая система, сложная система, структура, иерархия, декомпозиция системы, модули, информация и состояния системы, процесс, целенаправленная система и управление.

Сформулируем общие положения (принципы), обобщающие опыт человека при исследовании сложных систем:

· принцип конечной цели: абсолютный приоритет конечной (глобальной) цели,

· принцип единства: совместное рассмотрение системы как целого и как совокупности частей (элементов),

· принцип связности: рассмотрение любой части совместно с ее связями и окружением,

· принцип модульного построения: полезно выделение модулей в системе и рассмотрение ее как совокупности модулей,

· принцип иерархии: полезно введение иерархии частей и (или) их ранжирование,

· принцип функциональности: совместное рассмотрение структуры и функции с приоритетом функции над структурой,

· принцип развития: учет изменяемости системы, ее способности к развитию, расширению, замене частей, накапливанию информации,

· принцип децентрализации: сочетание в принимаемых решениях и управлении централизации и децентрализации,

· принцип неопределенности: учет неопределенностей и случайностей в системе.

Все принципы обладают очень высокой степенью общности. Для любой конкретной системы принципы должны быть конкретизированы. Многократное применение принципов системного подхода приводит к развитию особого (системного) типа мышления. Такое мышление характеризуется умением более правильно (адекватно) ставить, а нередко и решать задачи, связанные со сложными системами.

Системный анализ ставит перед системой ряд требований, несоблюдение которых может привести к неэффективному, а иногда и опасному по последствиям, результату.

Первое требование системного анализа — рассматривать совокупность элементов системы как одно целое; это есть запрет на рассмотрение системы как простого объединения элементов.

Второе требование заключается в признании того, что свойства системы не просто сумма свойств ее элементов. Система обладает особыми свойствами, которых может и не быть у отдельных элементов.

Важным атрибутом системы является ее эффективность. Теоретически доказано, что всегда существует функция ценности системы — в виде зависимости ее эффективности (это, как правило, экономический показатель) от условий построения и функционирования. Кроме того, эта функция ограничена, а, значит, имеет максимум. Максимум эффективности считается третьим требованием, предъявляемым к системе.

Четвертое требование запрещает рассматривать систему в отрыве от окружающей ее среды. Это означает обязательность учета внешних связей или, в более общем виде, требование рассматривать анализируемую систему как часть (подсистему) некоторой более общей системы.

Рассмотрение данной системы как части некоторой большей системы приводит к возможности деления данной системы на части, подсистемы. Если эти части оказываются сложными для анализа, с ними поступают точно также. Но в процессе такого деления нельзя нарушать предыдущие принципы — пока они соблюдены, деление оправдано в том смысле, что гарантирует применимость практических методов, приемов, алгоритмов решения задач системного анализа.

Все изложенное выше позволяет дать другую формулировку термина система: система — многоуровневая конструкция из взаимодействующих элементов, объединяемых в подсистемы нескольких уровней для достижения единой цели функционирования (целевой функции).

Системы и моделирование

Исследование системы по разным причинам (сложность, громоздкость, недоступность и т.д.) обычно заменяется формальным описанием тех ее особенностей, которые являются наиболее существенными. Такое формальное описание принято называть моделью.

Приведем пример, когда можно рассматривать и саму систему, и ее модель. Для исследования радиотехнического элемента можно подать на его входы все интересующие нас комбинации сигналов и снять соответствующие выходные сигналы. Это будет полный натурный эксперимент. Если же описать прохождение сигнала внутри элемента формальным образом (например, дифференциальными уравнениями), то мы сможем без самой системы определять выходные сигналы по входным. Это – работа с моделью.

С ростом сложности системы возможности натурного эксперимента резко падают. Он становится дорогим, трудоемким, длительным по времени, маловариантным. Тогда предпочтительнее работа с моделью. В ряде случаев мы вообще не имеем возможности наблюдать систему, но это не мешает ее познавать.

Рассмотрение вместо самой системы (явления, процесса) ее модели практически всегда несет идею упрощения. При моделировании фиксируются лишь те особенности системы, которые существенны для целей рассмотрения.

В разработке модели различают три стадии: первую (основную) –построение модели, вторую – пробную работу с ней, третью – корректировку и изменение по результатам пробной работы. После этого модель считается готовой к использованию. Построение принципиально новой модели носит характер открытия.

Достаточно сложным является и вопрос о том, кто должен создавать модель. Специалисту в данной практической области часто не хватает математических знаний, сведений о моделировании вообще, для сложных задач – знаний системного анализа. Прикладному математику трудно ориентироваться в предметной области. Их совместная работа над моделью будет иметь смысл лишь при полном понимании друг друга.

1.7. Принятие решений. Основные понятия и определения

Искусство принятия наилучших решений, основанное на опыте и интуиции, является сущностью любой сферы человеческой деятельности. Наука о выборе приемлемого варианта решения сложилась сравнительно недавно, а математической теории принятия решений – около 50 лет.

В последующие годы была создана прикладная теория статистических решений, позволяющая анализировать и решать широкий класс управленческих задач, связанных с ограниченным риском – проблемы выбора, размещения, распределения и т.п.

В настоящее время теория принятия решений применяется преимущественно для анализа тех деловых проблем, которые можно однозначно формализовать, а результаты исследования адекватно интерпретировать. Методы теории принятия решений используют в самых различных областях управления – при проектировании сложных технических и организационных систем, планировании развития городов, выборе программ развития экономики и энергетики регионов, организации новых экономических зон и т.п.

Необходимость использования подходов и методов теории принятия решений в управлении очевидна: быстрое развитие и усложнение экономических связей, выявление зависимости между отдельными сложными процессами и явлениями, которые раньше казались не связанными друг с другом, приводят к резкому возрастанию трудностей принятия обоснованных решений. Затраты на их осуществление непрерывно увеличиваются, последствия ошибок становятся все серьезнее, а обращение к профессиональному опыту и интуиции не всегда приводит к выбору наилучшей стратегии. Использование методов теории принятия решений позволяет решить эту проблему, причем быстро и с достаточной степенью точности.

Задачи принятия решений бывают совершенно разные по сложности математического аппарата. Рассмотрим достаточно простую задачу по безопасности жизнедеятельности, в которой требуется принять ответственное решение.

Пример 1.1. Оценить условия труда работника, непосредственно работающего с источником ионизирующего излучения, находящегося 100 дней в году в течение 1 часа на расстоянии 1м от радионуклида ⁵⁷Со, активностью 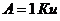(Ки – кюри).

Решение. Согласно нормам радиационной безопасности [19] предельная доза персонала, непосредственно работающего с источником ионизирующего излучения, составляет ПД=20 мЗв/год (мЗв – милизиверт).

Оценка условий труда сводится к определению годовой эффективной дозы и сопоставлении её с предельной дозой. При данных условиях облучается всё тело, поэтому согласно [9] годовая эффективная доза равна

,

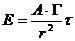где

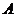– активность излучения, Бк (беккерель), ,

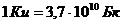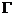– гамма-постоянная радионуклида, для 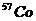по таблице из [8] 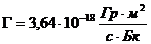(Гр – грей),

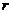– расстояние от радионуклида, м,

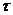– годовое время облучения, с.

Определим годовое время облучения:

.

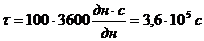Определим годовую эффективную дозу:

.

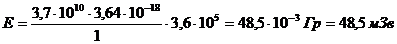Сравнивая полученное значение с предельной дозой, следует принять решение, что радиационная обстановка не соответствует нормам – условия труда недопустимы.

В данной задаче решение было принято на основе справочников и некоторых математических соотношений. В более сложных ситуациях этого часто оказывается не достаточно и требуется более серьезное исследование проблемы. Основными причинами могут быть отсутствие достоверных исходных данных, многовариантность, неопределенность ситуации, в которой принимается решение, наличие нескольких целей, сложность разработки математической модели.

Задача принятия решений должна быть направлена на определение наилучшего (оптимального) способа действий для достижения поставленной цели (целей). Под целью понимается идеальное представление желаемого результата деятельности. Если фактическое состояние не соответствует желаемому, то имеет место проблема. Выработка плана действий по устранению проблемы составляет сущность задачи принятия решений.

Проблема всегда связана с определенными условиями, которые обобщенно называют ситуацией. Совокупность проблемы и ситуации образует проблемную ситуацию. Выявление и описание проблемной ситуации дает исходную информацию для постановки задачи принятия решений.

Субъектом всякого решения является лицо, принимающее решение (ЛПР). Это лицо может быть одним человеком или несколькими. Для помощи ЛПР необходимы эксперты, осуществляющие сбор, анализ информации и формирование вариантов решений. Принятие решений происходит во времени, поэтому вводится понятие процесса принятия решений. Этот процесс состоит из последовательности этапов и процедур, направленных на устранение проблемной ситуации.

В процессе принятия решений формируются взаимоисключающие варианты – альтернативы 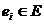, и оценивается их предпочтительность. Предпочтительность – это интегральная функция качества вариантов, основанная на объективном анализе (знании, опыте, проведении расчетов) и субъективном понимании их ценности. Предположим, что каждому варианту 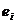однозначно соответствует количественная оценка 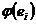. Это может быть, например, выигрыш, полезность, прибыль, надежность и др.

Основополагающий принцип теории принятия решений, сформулировали Дж.фон Нейман и О.Моргенштерн: лицо, принимающее решение, должно всегда выбирать альтернативу с максимально ожидаемой полезностью. Поэтому чем полезнее, предпочтительнее альтернатива – тем выше ее численная оценка.

Цель выбора состоит в определении альтернативы 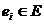, имеющей наибольшую предпочтительность, то есть такой альтернативы, для которой величина 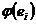является наибольшей. Противоположную ситуацию с оценкой затрат, потерь или риска можно исследовать точно так же путем минимизации оценки или, как это делается чаще, с помощью рассмотрения отрицательных величин выигрыша.

Выбор наилучшего варианта в соответствии с описанным способом не является, вообще говоря, однозначным, поскольку максимальная предпочтительность 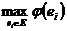может достигаться на нескольких альтернативах. Тогда возникает необходимость выбрать одно из нескольких одинаково хороших решений.

Рассмотренный случай принятия решения, при котором каждой альтернативе соответствует единственная оценка 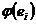, с точки зрения его практических применений является простейшим. На самом деле, в более реальных ситуациях каждой альтернативе 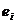вследствие различных внешних условий могут соответствовать различные, подчас противоречивые оценки. Тогда возникают многокритериальные задачи выбора решения и наиболее приемлемым, как правило, оказывается компромиссное решение.

Таким образом, под принятием решений понимается выбор наиболее предпочтительного решения из множества допустимых альтернатив.

Проблема принятия правильного, наилучшего в данной ситуации решения стоит перед человеком всегда. Искусством принятия решений должны владеть политики и военоначальники, менеджеры и руководители всех уровней, любой человек, имеющий минимальный жизненный опыт. Важность владения таким искусством бесспорна: от правильности выбранной альтернативы может зависеть не только судьба конкретного человека, но и общества в целом.

Трудности выбора решения могут скрываться в самой постановке задачи, если требуется достижение нереальных результатов: получение максимальной прибыли при минимальном риске, строительство в минимальные сроки при максимальном качестве, максимальный ущерб противнику в военных действиях при минимальных собственных потерях и т.п.

Принципы оптимальности в теории принятия решений прямо или косвенно должны отражать идеи устойчивости, выгодности и справедливости. Решение считается устойчивым с той точки зрения, что участникам процесса принятия решений не выгодно от него отклоняться. Такое решение называется равновесным, оно обеспечивает всем участникам максимально гарантированный выигрыш.

Если реализация принципов выгодности и устойчивости основана на исходных условиях задачи, то принцип справедливости устанавливается извне. Участники процесса принятия решений должны заранее их оговорить. Часто компромиссное решение, основанное на принципах справедливости, не совпадает с равновесным. В договоре между участниками может участвовать еще одно постороннее лицо: арбитр, который и предлагает компромиссное решение, отвечающее некоторым "принципам справедливости". Эти принципы часто формулируются в виде набора аксиом, отвечающим нормам морали общества и отраженным в существующем законодательстве.