Глава 1. Системный анализ и моделирование

Роль компьютерных технологий в системном анализе

Становление и развитие системного анализа характеризуется широчайшим проникновением вычислительной техники в процесс моделирования и принятия решений в сложной системе. Можно выделить три стороны взаимодействия человека и ЭВМ.

· Партнерство в выполнении операций, названное диалогом с ЭВМ. Суть диалога заключается в чередовании формализованных (ЭВМ) и неформализованных (человек) процедур, который обычно осуществляется специальными диалоговыми системами. Удачно организованные диалоговые системы значительно усиливают возможности как машины, так и человеческого мозга.

· Человек является создателем программных средств. Программные средства и другие компьютерные технологии выступают как средства исследования сложной системы. Именно человек оценивает решение или другую информацию, полученную с помощью вычислительной техники.

· Вычислительная техника, предназначенная для хранения, преобразования, изображения, расчетов и управления, является как неотъемлемой частью самих сложных систем, так и важнейшим средством их исследования.

Владение аппаратом системного анализа невозможно без использования ЭВМ, баз данных и знаний, вычислительных сетей, современных компьютерных технологий.

Определение системы. Основные понятия и базовые категории, характеризующие строение системы

Цель общей теории систем состоит в создании арсенала идей и средств, которые были бы в равной степени полезны специалистам во многих различных областях, таких как механика, физиология, электротехника, лингвистика. Эта цель может быть достигнута путем рассмотрения системы (которая может представлять собой живой организм, промышленное предприятие, управляемый снаряд) не через ее внутреннюю структуру, а через математические законы, определяющие ее наблюдаемое поведение. При использовании такого подхода, называемого методом «черного ящика», было найдено, что системы, представляющие совсем разные физические построения, могут все же быть охарактеризованы в одинаковых терминах и проанализированы с помощью одного и того же набора правил.

Термин системаиспользуют в тех случаях, когда хотят охарактеризовать исследуемый или проектируемый объект как нечто целое (единое) сложное, о котором невозможно сразу дать представление, показав его, изобразив графически или описав математическим выражением.

Определение понятия система изменялось по мере развития теории систем в течение 30 лет. Например, основоположник теории систем Берталанфи определял систему как комплекс взаимодействующих элементов или как совокупность элементов, находящихся в определённых отношениях друг с другом и средой. А. Холл определял систему как множество предметов вместе со связями между предметами и между их признаками. Позднее в определении системы появляется понятие цели. Так, в “Философском словаре”, система определяется как “совокупность элементов, находящихся в отношениях и связях между собой определённым образом и образующих некоторое целостное единство”.

В зависимости от количества учитываемых факторов и степени абстрактности существует несколько определений системы. Рассмотрим в символьной форме наиболее характерные из них:

1. S = ({m},{n},{r}),

где m – вещи, n – свойства, r – отношения. Система — множество вещей, свойств и отношений между ними.

2. S = ( UN, ST, BE, E),

где UN – элементы, ST – структура, BE – поведение, E – среда. Согласно этому определению система – множество элементов, образующих структуру и обеспечивающих определённое поведение в условиях окружающей среды.

3. S = (X, Y, Z, H, G),

где X – входы, Y – выходы, Z – состояния, H – операторы переходов из состояния в состояние, G – операторы выходов. Здесь система – множество входов, множество выходов, множество состояний, характеризуемых операторами переходов и выходов. Данное определение учитывает все основные компоненты, рассматриваемые в автоматике.

4. S = (P, R₀, R_j, E_x, PR, D_T, C, RD, E_f),

где P – цели и планы, R₀ – внешние ресурсы, R_j – внутренние ресурсы, E_x – исполнители, PR – процесс, D_T – помехи, C – контроль, RD – управление, E_f – эффект. Это определение ориентировано на организационные системы.

Важно отметить, что на разных этапах представления системы, в различных конкретных ситуациях можно пользоваться разными определениями. Причем, по мере уточнения представлений о системе или при переходе на другой уровень её исследования определение не только может, но и должно уточняться.

Рассмотрим основные понятия, характеризующие строение системы.

Под элементом принято понимать некоторый объект (материальный, энергетический, информационный), обладающий рядом важных для нас свойств, но внутреннее строение которого для нас безразлично.

Будем обозначать элементы через M, а всю совокупность элементов – через {M}. Принадлежность элемента совокупности принято записывать MÎ{M}.

Связью называется важный для целей рассмотрения обмен между элементами веществом, энергией, информацией.

Единичным актом связи выступает воздействие. Обозначая все воздействия элемента M₁ на элемент M₂ через x₁₂, элемента M₂ на M₁ – через x₂₁, можно изобразить связи графически (рис. 1.1).

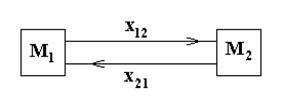
Рис. 1.1. Связь двух элементов

Связь характеризуетсянаправлением, силой и характером (или видом).По первым двум признакамсвязи можно разделить на: направленные или ненаправленные, сильные илислабые,по характерусвязи разделяются на: связи подчинения, связи порождения (генетические), равноправные, связи управления. Связи можно разделить также по месту приложения (внутренние и внешние), по направленности процессов в системе в целом или в отдельных ее подсистемах (прямые и обратные). Связи в конкретных системах могут быть одновременно охарактеризованы несколькими из названных признаков.

Важную роль в системах играет понятие обратной связи. Обратная связь может быть положительной, сохраняющей тенденции происходящих в системе изменений того или иного выходного параметра, и отрицательной – противодействующей тенденциям изменения выходного параметра, т. е. направленной на сохранение, стабилизацию требуемого значения параметра (например, стабилизацию выходного напряжения, или в системах организационного управления количества выпускаемой продукции, ее себестоимости и др.).

Уточним теперь понятие системы.

Системой будем называть совокупность элементов, обладающих следующими признаками:

· связями, которые позволяют соединить любые два элемента,

· свойством (назначением, функцией), отличным от свойств отдельных элементов.

Первый признак называется связностью, а второй признак – функцией системы. Применяя кортежное (последовательное в виде перечисления) определение системы, можно записать:

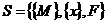, (1.1)

где 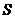– система, {M} – совокупность элементов в ней, {x} - совокупность связей, F – функция (новое свойство) системы. Запись (1.1) будем рассматривать как наиболее простое описание системы. Формы записи систем, приведенные выше, включают в себя большее количество членов кортежной последовательности.

Практически любой объект с определенной точки зрения может рассматриваться как система. Так системой можно считать радиотехническую плату, преобразующую входной сигнал в выходной. Для специалиста по элементной базе системой будет слюдяной конденсатор в этой плате, а для геолога – и сама слюда, имеющая достаточно сложное строение.

Системой с точки зрения механики является собранная из стержней стрела крана, или, например, труба газопровода. Элементами последней будут ее участки между сварными швами или опорами. Связи в данном случае имеют силовой (энергетический) характер – каждый элемент действует на соседний.

Важный класс сложных систем (с разнородными элементами и связями) образуют автоматизированные системы с определяющей ролью элементов двух типов: в виде технических средств и в виде действий человека. Символьная запись автоматизированной системы:

,

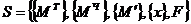где 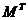– технические средства, в первую очередь, ЭВМ, 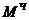– решения и другие действия человека, 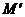– остальные элементы в системе. В совокупности 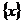в этом случае могут быть выделены связи между человеком и техникой .

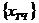Система может быть разделена на элементы не сразу, а последовательным расчленением на более крупные (чем элементы) составляющие: подсистемы или компоненты.

Понятие подсистема подразумевает, что выделяется относительно независимая часть системы, обладающая свойствами системы и другими свойствами. Если же части системы не обладают такими свойствами, а представляют собой просто совокупности однородных элементов, то такие части принято называтькомпонентами.

Системы и моделирование

Исследование системы по разным причинам (сложность, громоздкость, недоступность и т.д.) обычно заменяется формальным описанием тех ее особенностей, которые являются наиболее существенными. Такое формальное описание принято называть моделью.

Приведем пример, когда можно рассматривать и саму систему, и ее модель. Для исследования радиотехнического элемента можно подать на его входы все интересующие нас комбинации сигналов и снять соответствующие выходные сигналы. Это будет полный натурный эксперимент. Если же описать прохождение сигнала внутри элемента формальным образом (например, дифференциальными уравнениями), то мы сможем без самой системы определять выходные сигналы по входным. Это – работа с моделью.

С ростом сложности системы возможности натурного эксперимента резко падают. Он становится дорогим, трудоемким, длительным по времени, маловариантным. Тогда предпочтительнее работа с моделью. В ряде случаев мы вообще не имеем возможности наблюдать систему, но это не мешает ее познавать.

Рассмотрение вместо самой системы (явления, процесса) ее модели практически всегда несет идею упрощения. При моделировании фиксируются лишь те особенности системы, которые существенны для целей рассмотрения.

В разработке модели различают три стадии: первую (основную) –построение модели, вторую – пробную работу с ней, третью – корректировку и изменение по результатам пробной работы. После этого модель считается готовой к использованию. Построение принципиально новой модели носит характер открытия.

Достаточно сложным является и вопрос о том, кто должен создавать модель. Специалисту в данной практической области часто не хватает математических знаний, сведений о моделировании вообще, для сложных задач – знаний системного анализа. Прикладному математику трудно ориентироваться в предметной области. Их совместная работа над моделью будет иметь смысл лишь при полном понимании друг друга.

1.7. Принятие решений. Основные понятия и определения

Искусство принятия наилучших решений, основанное на опыте и интуиции, является сущностью любой сферы человеческой деятельности. Наука о выборе приемлемого варианта решения сложилась сравнительно недавно, а математической теории принятия решений – около 50 лет.

В последующие годы была создана прикладная теория статистических решений, позволяющая анализировать и решать широкий класс управленческих задач, связанных с ограниченным риском – проблемы выбора, размещения, распределения и т.п.

В настоящее время теория принятия решений применяется преимущественно для анализа тех деловых проблем, которые можно однозначно формализовать, а результаты исследования адекватно интерпретировать. Методы теории принятия решений используют в самых различных областях управления – при проектировании сложных технических и организационных систем, планировании развития городов, выборе программ развития экономики и энергетики регионов, организации новых экономических зон и т.п.

Необходимость использования подходов и методов теории принятия решений в управлении очевидна: быстрое развитие и усложнение экономических связей, выявление зависимости между отдельными сложными процессами и явлениями, которые раньше казались не связанными друг с другом, приводят к резкому возрастанию трудностей принятия обоснованных решений. Затраты на их осуществление непрерывно увеличиваются, последствия ошибок становятся все серьезнее, а обращение к профессиональному опыту и интуиции не всегда приводит к выбору наилучшей стратегии. Использование методов теории принятия решений позволяет решить эту проблему, причем быстро и с достаточной степенью точности.

Задачи принятия решений бывают совершенно разные по сложности математического аппарата. Рассмотрим достаточно простую задачу по безопасности жизнедеятельности, в которой требуется принять ответственное решение.

Пример 1.1. Оценить условия труда работника, непосредственно работающего с источником ионизирующего излучения, находящегося 100 дней в году в течение 1 часа на расстоянии 1м от радионуклида ⁵⁷Со, активностью 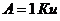(Ки – кюри).

Решение. Согласно нормам радиационной безопасности [19] предельная доза персонала, непосредственно работающего с источником ионизирующего излучения, составляет ПД=20 мЗв/год (мЗв – милизиверт).

Оценка условий труда сводится к определению годовой эффективной дозы и сопоставлении её с предельной дозой. При данных условиях облучается всё тело, поэтому согласно [9] годовая эффективная доза равна

,

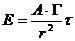где

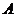– активность излучения, Бк (беккерель), ,

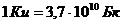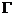– гамма-постоянная радионуклида, для по таблице из [8] 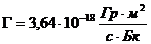(Гр – грей),

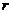– расстояние от радионуклида, м,

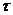– годовое время облучения, с.

Определим годовое время облучения:

.

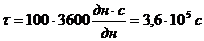Определим годовую эффективную дозу:

.

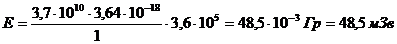Сравнивая полученное значение с предельной дозой, следует принять решение, что радиационная обстановка не соответствует нормам – условия труда недопустимы.

В данной задаче решение было принято на основе справочников и некоторых математических соотношений. В более сложных ситуациях этого часто оказывается не достаточно и требуется более серьезное исследование проблемы. Основными причинами могут быть отсутствие достоверных исходных данных, многовариантность, неопределенность ситуации, в которой принимается решение, наличие нескольких целей, сложность разработки математической модели.

Задача принятия решений должна быть направлена на определение наилучшего (оптимального) способа действий для достижения поставленной цели (целей). Под целью понимается идеальное представление желаемого результата деятельности. Если фактическое состояние не соответствует желаемому, то имеет место проблема. Выработка плана действий по устранению проблемы составляет сущность задачи принятия решений.

Проблема всегда связана с определенными условиями, которые обобщенно называют ситуацией. Совокупность проблемы и ситуации образует проблемную ситуацию. Выявление и описание проблемной ситуации дает исходную информацию для постановки задачи принятия решений.

Субъектом всякого решения является лицо, принимающее решение (ЛПР). Это лицо может быть одним человеком или несколькими. Для помощи ЛПР необходимы эксперты, осуществляющие сбор, анализ информации и формирование вариантов решений. Принятие решений происходит во времени, поэтому вводится понятие процесса принятия решений. Этот процесс состоит из последовательности этапов и процедур, направленных на устранение проблемной ситуации.

В процессе принятия решений формируются взаимоисключающие варианты – альтернативы 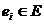, и оценивается их предпочтительность. Предпочтительность – это интегральная функция качества вариантов, основанная на объективном анализе (знании, опыте, проведении расчетов) и субъективном понимании их ценности. Предположим, что каждому варианту 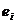однозначно соответствует количественная оценка 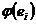. Это может быть, например, выигрыш, полезность, прибыль, надежность и др.

Основополагающий принцип теории принятия решений, сформулировали Дж.фон Нейман и О.Моргенштерн: лицо, принимающее решение, должно всегда выбирать альтернативу с максимально ожидаемой полезностью. Поэтому чем полезнее, предпочтительнее альтернатива – тем выше ее численная оценка.

Цель выбора состоит в определении альтернативы 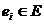, имеющей наибольшую предпочтительность, то есть такой альтернативы, для которой величина 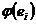является наибольшей. Противоположную ситуацию с оценкой затрат, потерь или риска можно исследовать точно так же путем минимизации оценки или, как это делается чаще, с помощью рассмотрения отрицательных величин выигрыша.

Выбор наилучшего варианта в соответствии с описанным способом не является, вообще говоря, однозначным, поскольку максимальная предпочтительность 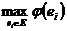может достигаться на нескольких альтернативах. Тогда возникает необходимость выбрать одно из нескольких одинаково хороших решений.

Рассмотренный случай принятия решения, при котором каждой альтернативе соответствует единственная оценка 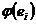, с точки зрения его практических применений является простейшим. На самом деле, в более реальных ситуациях каждой альтернативе 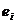вследствие различных внешних условий могут соответствовать различные, подчас противоречивые оценки. Тогда возникают многокритериальные задачи выбора решения и наиболее приемлемым, как правило, оказывается компромиссное решение.

Таким образом, под принятием решений понимается выбор наиболее предпочтительного решения из множества допустимых альтернатив.

Проблема принятия правильного, наилучшего в данной ситуации решения стоит перед человеком всегда. Искусством принятия решений должны владеть политики и военоначальники, менеджеры и руководители всех уровней, любой человек, имеющий минимальный жизненный опыт. Важность владения таким искусством бесспорна: от правильности выбранной альтернативы может зависеть не только судьба конкретного человека, но и общества в целом.

Трудности выбора решения могут скрываться в самой постановке задачи, если требуется достижение нереальных результатов: получение максимальной прибыли при минимальном риске, строительство в минимальные сроки при максимальном качестве, максимальный ущерб противнику в военных действиях при минимальных собственных потерях и т.п.

Принципы оптимальности в теории принятия решений прямо или косвенно должны отражать идеи устойчивости, выгодности и справедливости. Решение считается устойчивым с той точки зрения, что участникам процесса принятия решений не выгодно от него отклоняться. Такое решение называется равновесным, оно обеспечивает всем участникам максимально гарантированный выигрыш.

Если реализация принципов выгодности и устойчивости основана на исходных условиях задачи, то принцип справедливости устанавливается извне. Участники процесса принятия решений должны заранее их оговорить. Часто компромиссное решение, основанное на принципах справедливости, не совпадает с равновесным. В договоре между участниками может участвовать еще одно постороннее лицо: арбитр, который и предлагает компромиссное решение, отвечающее некоторым "принципам справедливости". Эти принципы часто формулируются в виде набора аксиом, отвечающим нормам морали общества и отраженным в существующем законодательстве.

Требования, предъявляемые к математическим моделям

Основными требованиями, предъявляемыми к математическим моделям, являются требования адекватности, непротиворечивости, универсальности и экономичности.

Модель считается адекватной, если она отражает заданные свойства объекта с приемлемой точностью.

Непротиворечивость модели заключается в том, что она не должна содержать зависимостей, которые бы противоречили друг другу.

Универсальность модели состоит в том, что она служит математическим описанием для целого класса (близких или далеких по характеру) задач. Например, дифференциальные уравнения являются математическими моделями для колебаний математического маятника, описывают колебательные процессы в механической и электрической системах, описывают колебания арки моста, процессы, протекающие в струнах музыкальных инструментов, и т.д. Универсальность определяется также числом и составом учитываемых в модели входных и выходных параметров.

Экономичность модели характеризуется затратами вычислительных ресурсов для ее реализации, а именно, затратами машинного времени и памяти. Эти затраты зависят как от особенностей выбранной модели, так и от методов решения соответствующих математических задач.

Требования адекватности и универсальности, с одной стороны, и высокой экономичности, с другой, очевидно, являются противоречивыми. Поэтому для удовлетворения всем указанным требованиям разработчик модели должен идти на компромисс.

Моделирование систем на ЭВМ

Эффективность экспериментальных исследований сложных систем оказывается крайне низкой, поскольку проведение натурных экспериментов с реальной системой либо требует больших материальных затрат и значительного времени, либо вообще практически невозможно, например, на этапе проектирования, когда реальная система отсутствует.

Появление современных ЭВМ явилось решающим условием широкого внедрения методов математического моделирования в исследование сложных систем вообще, и информационных систем, в частности. Математические модели и аналитические методы их исследования могут решить многие проблемы, определяющие качество функционирования сложных систем. Однако, одновременно с этим появились причины, препятствующие применению в инженерной практике аналитических методов исследования систем:

- наличие случайных зависимостей между параметрами, характеризующие процессы в системе,

- необходимость учета стохастических свойств системы.

Это приводит к необходимости разработки более адекватных математических моделей. С этой целью шире стали применяться методы имитационного моделирования.

Современные ЭВМ можно разделить на две группы: универсальные, предназначенные для выполнения расчетных работ и управляющие, предназначенные, прежде всего, для управления объектами в реальном масштабе времени. Управляющие ЭВМ могут быть использованы как для управления технологическими процессами, так и для реализации имитационных моделей. Эксперимент с имитационной моделью требует серьезной подготовки [25], поэтому имитационная модель характеризуется наличием математического, программного, информационного, технического и других видов обеспечения.

Математическое обеспечение имитационных моделей включает в себя совокупность математических соотношений, описывающих поведение реального объекта, совокупность алгоритмов, обеспечивающих работу с моделью: алгоритмы ввода исходных данных, имитации, вывода, обработки.

Программное обеспечение включает в себя совокупность программ: планирования эксперимента, имитационной модели, проведения эксперимента, обработки и интерпретации результатов.

Информационное обеспечение включает в себя средства и технологию организации и реорганизации базы данных моделирования, формы документов, описывающих процесс моделирования и его результаты.

Техническое обеспечение имитационной модели включает в себя средства вычислительной техники, связи и диалоговую систему обмена между оператором и ЭВМ, ввода и вывода информации, управления проведением эксперимента.

Таким, образом, имитационная система может рассматриваться как машинный аналог сложного реального процесса. Он позволяет заменить эксперимент с реальным процессом функционирования системы экспериментом с математической моделью этого процесса в ЭВМ.

Имитационное моделирование на ЭВМ имеет достоинства и недостатки, проявляющиеся в конкретных приложениях. Основные достоинства:

- машинный эксперимент с имитационной моделью дает возможность исследовать особенности процесса функционирования системы в любых условиях,

- применение ЭВМ в имитационном эксперименте существенно сокращает продолжительность испытаний по сравнению с натурным экспериментом,

- имитационная модель позволяет включать результаты натурных испытаний реальной системы для проведения дальнейших исследований,

- имитационная модель обладает гибкостью варьирования структуры, алгоритмов и параметров моделируемой системы, что важно с точки зрения поиска оптимального варианта системы,

- имитационное моделирование сложных систем часто является единственным практически реализуемым методом исследования процесса функционирования таких систем на этапе их проектирования.

Основным недостатком имитационного моделирования на ЭВМ является то, что решение, полученное при анализе имитационной модели, всегда носит частный характер. Поэтому для полного анализа характеристик процесса функционирования системы приходится многократно воспроизводить имитационный эксперимент, варьируя исходные данные задачи. При этом, как следствие, возникает увеличение затрат машинного времени на проведение эксперимента с имитационной моделью. Эффективность имитационного моделирования может оцениваться рядом критериев, в том числе точностью и достоверностью результатов моделирования, временем построения и работы с моделью, затратами машинных ресурсов (времени и памяти), стоимостью разработки и эксплуатации модели.

Специалисты в области проектирования, исследования и эксплуатации больших систем должны в совершенстве знать методологию машинного моделирования, сложившуюся к настоящему времени, чтобы быть готовыми к появлению ЭВМ следующих поколений, которые позволят сделать следующие шаги в направлении автоматизации построения моделей и использования имитационного моделирования систем.

Глава 1. Системный анализ и моделирование

1.1. Системный анализ как научная дисциплина

В научных исследованиях и технических разработках, на производстве, в социальных областях мы постоянно сталкиваемся с совокупностями объектов, которые принять называть сложными системами. Их отличительные особенности – это многочисленные и разные по типу связи между отдельными элементами системы и наличие у системы функции (назначения), которой нет у составляющих ее частей. Каждая конкретная система имеет только ей присущую организацию, то есть определенный порядок, внутренние свойства связей между элементами, направленность на выполнение функции системы. Примерами систем являются человек, трактор, ЛТА.

Задача изучения системы и ее организации – понять поведение системы (это задача анализа). Задачей более высокого уровня выступает создание нужной нам системы и управление ею (это задача синтеза). Ведущей операцией при этом является принятие решения, то есть некоторый формализованный или неформализованный выбор, позволяющий достичь некоторой цели или продвинуться в ее направлении. Принятие решений в сложной системе производится техническим средством или человеком и основано на сравнении и оценке вариантов действий. Изучение процедур принятия решения и связанной с этим организации системы составляют актуальную проблему создания и эксплуатации сложных систем. Решение указанной проблемы невозможно без применения системного анализа.

В современном понимании системный анализ – это научная дисциплина, занимающаяся разработкой методов и моделей анализа и синтеза систем, а также проблемами принятия решений в условиях анализа большого количества информации различной природы.

В системном анализе могут быть выделены методология, аппаратная реализация, опыт применения в различных областях науки и практики.

Методология есть базовое начало системного анализа. Она включает определения используемых понятий, принципы системного подхода, а также постановку и общую характеристику основных проблем организации системных исследований.

Под аппаратной реализацией понимаются стандартные приемы моделирования сложных систем и общие способы работы с моделями.

Опыт применения системного анализа в различных областях в настоящее время чрезвычайно велик. Важнейшими областями применения являются научно-технические разработки, экономика, биология, экология, военное дело, социология, психология, управление государством и регионами, обучение, выработка научного мировоззрения и др.

1.2. Взаимосвязь системного анализа со смежными дисциплинами

В связи с развитием науки образовалась сложная иерархия узкоспециализированных дисциплин. В конце 19-го – начале 20 в. появилась жизненная необходимость в выполнении комплексных проектов. Появились новые науки: «Кибернетика», «Теория информации», «Исследование операций» и др. Начиная с 50-х годов 20 в. стала формироваться общенаучная дисциплина «Общая теория систем» или «Системология». Системный анализ тесно связан с этими дисциплинами.

Общая теория систем занимается всевозможными вопросами исследования систем, а не только проблемами принятия решений, как это делается в системном анализе. В этом смысле системный анализ составляет существенную, важную в прикладном отношении часть теории систем. Значительным достижением по теории систем выступают теория организации русского экономиста Александра Богданова и общая теория систем американского биолога Людвига фон Берталанфи (изобретатель модели человеческого мозга – персифтона). Истоки образования общей теории систем относят к 1954 г., когда группа из четырех ученых по моделированию в биологии, психологии и экономике образовали общество системных исследований. Достаточно сформировавшейся является математическая теория сложных систем (Р.Калман, М.Месарович, Н.П.Бусленко, Г.С.Поспелов, В.М.Глушков). В нашей стране эти работы особенно интенсивно стали выполняться после 60 г., когда был снят запрет на кибернетику.

Частью теории систем следует считать кибернетику, которая традиционно определяется как наука об управлении, связи и переработке информации. Понятие управление близко, но не совпадает с принятием решения. Системный анализ перенял у кибернетики значительное количество терминов, такие как входы и выходы в системе, модули, потоки информации, структурные схемы.

Системотехника определяется и как применение теории систем к области техники, и как применение техники, прежде всего вычислительной, при исследовании сложных систем. Еще более узко – как использование системного анализа для проектирования ЭВМ и сетей ЭВМ, а также создания их программного обеспечения.

Понятие информатика чаще всего понимается как исследование проблем хранения, использования и преобразования информации при помощи средств вычислительной техники. Эта ветвь знания является одной из основ при проведении системного анализа при помощи ЭВМ.

В отечественной научной литературе исследование операций традиционно обозначает математическую дисциплину, занимающуюся исследованием математических моделей для выбора параметров, оптимизирующих некоторый критерий (или критерии) эффективности системы. Системный анализ может сводиться к решению ряда задач исследования операций, но обладает свойствами, не охватываемыми этой дисциплиной. В литературе США термин «исследование операций» не является чисто математическим и приближается к термину «системный анализ».

Системный анализ взаимодействует со всеми перечисленными дисциплинами, а наиболее тесно связан с теорией систем. Системный анализ в значительной мере опирается на такие ее части, как структуризация, иерархия в системе, связь системы с «не системой» (внешней средой), законы протекания процессов в системе, эволюция системы, в том числе, самоорганизация. Специфические части самого системного анализа: целенаправленная система, выделение действий и приемы работы с ними, сочетание формализованных и неформализованных процедур, действия лица, принимающего решения, системные вопросы информатики. Широкая опора на исследование операций, которая имеет место, по крайней мере, в технике и экономике, приводит его к таким математическим разделам, как постановка задач принятия решения, описание множества альтернатив, методы и модели задач оптимизации, исследование многокритериальных задач и др.