Операции с рациональными неотрицательными числами

Операции с числами в множестве 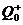также вводятся на основе системы аксиом.

Аксиома III. Под суммой двух дробей 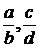понимается дробь вида 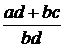. Обозначается: .

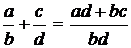Сумма двух дробей обладает свойствами:

а) коммутативности: ;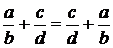

б) ассоциативности: ;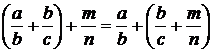

в) аддитивности : ;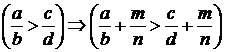

г) монотонности: .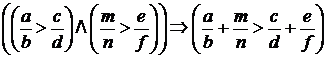

Действительно, если 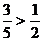(так как 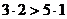), прибавим к обеим частям дробь 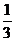, 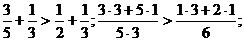откуда 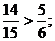(так как 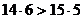), неравенство сохраняется.

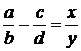Вычитание двух дробей в вводится по определению, как нахождение одного из слагаемых по известным сумме и второму слагаемому. Обозначается: , где 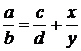, 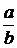-уменьшаемое, 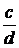-вычитаемое, 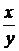- разность. Вычитание двух дробей возможно только при .

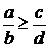Аксиома 1V. Под произведением двух дробей 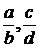понимается дробь вида 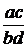. Обозначается: .

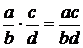Произведение двух дробей обладает свойствами:

а) коммутативности: ;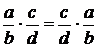

б) ассоциативности: ;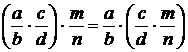

в) дистрибутивности относительно суммы и разности дробей: ;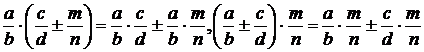

г) мультипликативности: ;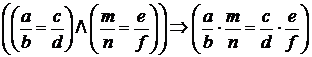

д) монотонности : .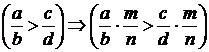

Деление двух дробей вводится также по определению, как нахождение одного из сомножителей по известным произведению и второму сомножителю. Обозначается : 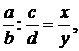где 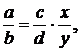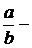делимое, 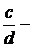делитель, 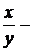частное. Деление двух дробей возможно всегда, т.е. частное дробей всегда существует.

Аксиома V. 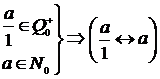. Аксиома V осуществляет связь между множествам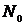и и , из этой аксиомы следует, что числа и числа 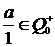обладают одними и теми же свойствами.

Например, пусть 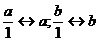, тогда:

1)

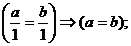
2) 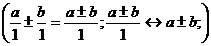, т.е. ;

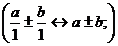3) 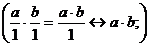, т.е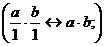

4) Пусть 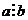, тогда a=bq, или 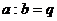. С другой стороны:

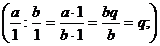, т.е. имеем 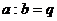и 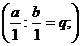, поэтому

.

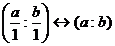Следствие: частное от деления двух целых неотрицательных чисел можно выразить неотрицательным рациональным числом, у которого первая компонента – это делимое, а вторая компонента – это делитель.

Действительно: 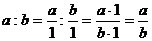, или .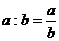

ТЕМА XII – ОСНОВНЫЕ ПОНЯТИЯ ВЕЛИЧИНЫ

Общее понятие величины.

Длина отрезка как величина.

Площадь плоской фигуры как величина.

Общее понятие величины

Геометрические фигуры обладают некоторыми свойствами, эти свойства обладают особенностями.

Во – первых, отмечается наличиеили отсутствие конкретного свойства у данной геометрической фигуры: ограниченность (отрезка), равенство всех сторон у квадрата.

Во – вторых, про некоторые свойства геометрических фигур можно утверждать, что они обладают этими свойствами в большем или меньшем количестве. Даже можно утверждать, какое количество единиц данного свойства содержит эта фигура. К таким свойствам относятся:

- свойство отрезка иметь длину;

- свойство плоской фигуры иметь площадь;

- свойство тела иметь объем.

При рассмотрении такого свойства фигур ставятся задачи:

1) Когда следует считать, обладает или нет фигура интересующим нас свойством?

2) Каким способом можно определить количество этого свойства у данной фигуры?

Другими словами: каким способом можно сопоставить данной фигуре некоторое неотрицательное число, показывающее сколько единиц данного свойства имеется у фигуры. Если фигура обладает одним из указанных свойств, то количество этого свойства называют:

- мера длины;

- мера площади,

- мера объема, или просто: длина, площадь, объем.

Длина, площадь, объем – это числовые характеристики геометрических фигур. Нахождение численного значения данной величины фигуры называется измерением.

Опр. 1.Геометрическая фигура обладает свойством величины, если ей можно по определенному закону поставить в соответствие некоторую числовую характеристику, обладающую свойствами инвариантности и аддитивности.

Замечание 1. Смысл терминов «инвариантность» и «аддитивность» рассмотрим позже.

Сформулируем определение понятия величины, опираясь на аксиоматический метод разработки теории.

1) Зададим некоторое множество элементов – S.

2) В построенном множестве S введем отношения между элементами:

- отношение эквивалентности;

- состоять из (т.е. элемент «а» состоит из элементов «b» и «с»).

Опр.2.На множестве S определена величина, если можно поставить в соответствие неотрицательное действительное число f(a) так, чтобы выполнялись условия:

(1)

(2) - свойство аддитивности (add – сложить, прибавить);

(3) некоторому элементу «е» из множества S соответствует число единица;

(4) пусть в множестве S установлено два вида соответствий (два вида измерений), удовлетворяющих условиям (1), (2), (3).

I – элементу соответствует число

II – элементу соответствует число ,

тогда существует число к>0 такое, что - свойство инвариантности (неизменности).

Длина отрезка как величина

Пусть задано некоторое множество отрезков S={a,b,c,…m}, Введем в этом множестве отношение , означающее равенство отрезков a=b, выражение означает, что отрезок «а» состоит из отрезков «b» и «с». обозначим через некоторое положительное действительное число, назовем его мерой отрезка «а».

Опр. 3. Число называется длиной отрезка , если для можно поставить в соответствие некоторое число так, чтобы выполнялись условия:

(1) = );

(2) ; (свойство аддитивности);

(3) - существует единичный отрезок «е», которому сопоставляется число единица;

(4) если для отрезков множества S существуют два единичных отрезка «е» и «f», то можно найти такое число , что (свойство инвариантности).

Например, е=1см, f=1м, и пусть см, м, тогда , т.е. к=0,01.

Из предыдущего имеем следствия:

1) - при замене единичного отрезка «е» на равный ему единичный отрезок «f» длина отрезка не изменится.

2) - если меры отрезков одинаковы, то отрезки измерены одним и тем же единичным отрезком.