Возникновение и развитие аксиоматической теории геометрии Евклида

Уже в древние века набралось достаточно математических сведений о методах учета при товарообороте, об измерении участков земли, однако эти сведения были разрозненными, часто не связанными между собой, что создавало трудности в развитии общества. Встает вопрос о приведении математических сведений об окружающем мире в строгую систему.

В Ш веке до н.э древнегреческому ученому Евклидупервому удалось осуществить теоретическую обработку математического материала. Он написал книгу под названием «Начала», в которой сделал попытку впервые привести в некоторую систему известные к тому времени геометрические сведения. В средние века «Начала» были единственным научным источником по геометрии, эта книга явилась основой для разработки традиционного школьного курса геометрии до настоящего времени.

«Начала» состоят из 13 книг, содержащих научные сведения по планиметрии, стереометрии и арифметике в геометрическом изложении. Евклид, как ученый и философ, понимал, что для разработки научной теории математики (геометрии), необходимо выделить какие – то исходные, первоначальные понятия, с которыми позже можно будет работать. Поэтому в каждой совей книге изложение материала начинается со знакомства с математическими понятиями, которые читателю встречаются впервые. Так в первой книге в начале приводятся 23 определения понятий, которые, по его мнению, должны лежать в основе математики. Так Евклид сделал попытку дать определения основных понятий геометрии, например:

(1) Точка есть то, что не имеет частей.

(2) Прямая линия есть та, которая равно расположена по отношению к точкам на ней.

Далее Евклид формулирует предложения, описывающие отношения между объектами и принимаемые без доказательства, их он делит на две группы: аксиомы и постулаты. Аксиомы носят общий характер, а постулаты относятся только к геометрическим объектам, например:

А I. Равные порознь третьему равны между собой.

А II. Если к равным прибавим равные, получим равные, и др. или

П I. От всякой точки до всякой другой точки можно провести линию.

П IV. Все прямые углы равны между собой.

П V. Если при пересечении двух прямых, лежащих в одной плоскости, третьей, сумма двух внутренних односторонних углов не равна удвоенному прямому углу, то данные две прямые пересекаются и именно с той стороны, где эта сумма меньше .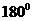

Далее следуют предложения (теоремы), расположенные в строгой последовательности так, что доказательство следующего предложения опирается на предыдущее.

Хотя «Начала» Евклида были долго образцом для сравнения, они не достигают уровня современной строгости. Второй этап развития аксиоматического метода относится к началу XIX века, когда крупнейшие математики, анализируя работу Евклида, выявили в ней крупные недостатки.

Во – первых, нечетко выделены первичные, неопределяемые понятия, например, если это определение является определением через род и видовое отличие, то понятия «то» и « часть» должны быть определены.

Во – вторых, ни в «Началах», ни в любой другой работе современников не раскрывается смысл «логического доказательства». Часто доказательства представляли смесь логических умозаключений с интуитивными догадками и ссылками на геометрическую наглядность. Строгое доказательство без наглядности и интуиции Евклид и не мог построить из – за недостаточной базы основных предложений (теорем, аксиом).

В – третьих, стоял вопрос о сокращении числа постулатов и аксиом, путем решения этого вопроса было превращение некоторых аксиом в теоремы (т.е. их доказательство). И действительно, Д. Гильберт в 1898 году доказал теорему о равенстве всех прямых углов (у Евклида этот факт подается как аксиома).

Наконец, особое внимание было уделено пятому постулату. В процессе развития геометрии – науки этот постулат преобразовался в известную из курса геометрии основной школы аксиому о параллельных прямых: через данную точку «Р» , не лежащую на данной прямой «а», можно провести не более одной прямой, не пересекающей прямую «а». Такие прямые впоследствии получили название параллельных прямых. По своей структуре пятый постулат Евклида громоздкий по своей формулировке; расположен в конце списка постулатов, большая часть геометрического материала в изложении Евклида не зависит от него (он используется Евклидом только после 29 предложения). Геометрический раздел математики разделился как бы на две части: первая часть (включая 29 предложение) впоследствии получила название «абсолютной геометрии», вторая часть содержит предложения, которые не могут быть доказаны без использования пятого постулата: теория подобия, теория пропорциональных отрезков, теорема о сумме углов треугольника ( 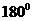) и др. Дополнение «абсолютной геометрии»

второй частью геометрического материала образовало Евклидову геометрию. Но перед учеными стоял вопрос: нельзя ли пятый постулат доказать, (т.е. считать пятый постулат теоремой)? Доказательством пятого постулата занимались крупнейшие ученые того времени (Д.Саккери, И.Г. Ламберт, Ф. Гаусс, Я. Больяи и др.). Все попытки доказательства постулата были безуспешными. И только наш соотечественник, профессор Казанского Университета Н. И. Лобачевский (1792 – 1856 г.г.) добился значительных результатов.

Выше было показано, что пятый постулат эквивалентен современной аксиоме о параллельных: через точку вне прямой проходит не более одной прямой, не пересекающей данную прямую. Н.И. Лобачевский заменил пятый постулат предложением о том, что через точку вне данной прямой проходит по крайней мере две прямых, не пересекающих данную прямую. Получив новую систему аксиом, Н. И. Лобачевский рассчитывал, что в процессе доказательства следующих свойств, следствий из «неверной» системы аксиом будут получены противоречии, которые и докажут пятый постулат. Однако, продолжая разработку теории, н. И. Лобачевский получил стройную теорию, фактически новый раздел науки, который позже назвали «геометрией Лобачевского» и которая сыграла большую роль в дальнейшем развитии математики. Интересными фактами в этой теории являются: (1) два перпендикуляра к одной прямой беспредельно расходятся (в Евклидовой геометрии они параллельны); (2) не существует подобных фигур (в Евклидовой геометрии – есть теория подобия фигур) и др.

В XIX веке в процессе исследования достижений Евклида и анализа его ошибок и недоработок в разработке аксиоматической теории немецкий математик Д Гильберт пересмотрел всю аксиоматику Евклида, переработал раздел геометрии в соответствии с идеями того времени и построил аксиоматическую теорию геометрии, которая называется «геометрией Евклида».

Соответствующая аксиоматика была разработана Д.Гильбертом и для пространства.

Разработанная Д. Гильбертом аксиоматическая теория геометрии называется «геометрией Евклида», ее изучают на средней ступени образования, с элементами геометрии Евклида знакомятся и учащиеся начального образования.

ТЕМА X – ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИИ ЕВКЛИДА

1. Система аксиом Д.Гильберта на плоскости (геометрия Евклида)