Понятие уравнения, свойства уравнений

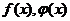По определению 1, математическое выражение – это последовательность букв латинского алфавита, чисел, знаков действий и скобок, например, . Если выражение содержит буквы латинского алфавита, обычно обозначающие переменные (x;y;z…), то имеем выражение с переменными (или с одной переменной). Выражение с переменной обозначается и т. д.

Если два выражения 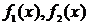с переменной соединить знаками равенства (=), то получим равенство с переменной. Например, если 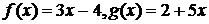то 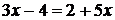- равенство с переменной, Равенство с переменной называют уравнением с одной переменной.

Опр.5.Уравнением с одной переменной на числовом множестве 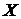называется предикат вида .

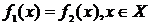Множество истинности Т этого предиката называется множеством решений уравнения. Решить уравнение - это значит найти его множество истинности Т. Если уравнение 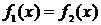становится истинным при любых значениях переменной, то уравнение является тождеством. Иначе говоря, в тождестве множество истинности Т совпадает с областью определения Х. Например, уравнение 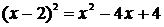истинно при любых значениях переменной , поэтому это уравнение – тождество. Говорят, что выражения 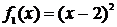и 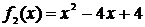тождественно равны: 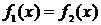. Замена выражения 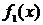тождественно равным ему выражением 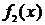называется тождественным преобразованием выражения 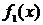в выражение .

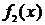Опр.6. Равносильными называются два уравнения 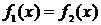(1) и 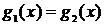(2), если каждое решение уравнения (1) является решением уравнения (2), и обратно, каждое решение уравнения (2) является решением уравнения (1). Иначе: уравнения (1) и (2) равносильны, если множества их истинности совпадают.

Обозначается: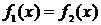

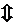
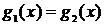или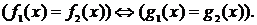

Теорема 1. Если к обеим частям уравнения 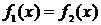, заданного на множестве Х, прибавить выражение , имеющее смысл при всех допустимых значениях переменной, то получим уравнение, равносильное данному. Обозначается: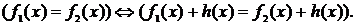

Эта теорема применяется для решения уравнений. Например, при решении линейного уравнения 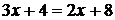прибавим к обеим частям выражение ( 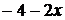): 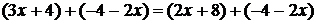, откуда .

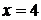На практике используют более короткие пути решения:

(1) В курсе математики средней школы для решения линейных уравнений применяют следствие из теоремы 1: перенос члена уравнения из одной части равенства в другую с противоположным знаком. Например, в уравнении 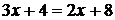перенесём число 4 в правую часть равенства со знаком минус (-), выражение 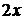перенесем в левую часть равенства также со знаком минус(-), получаем: 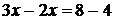, откуда .

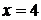(2) В курсе математики начальной школы для решения линейного уравнения используют зависимость между компонентами действий. Например, в уравнении 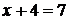неизвестная переменная - первое слагаемое, число 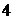-второе слагаемое, число -сумма, по свойствам суммы неизвестное слагаемое равно разности суммы и второго слагаемого : .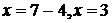

Квадратное уравнение 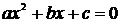решается по формуле:

.

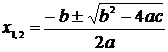Например, надо решить квадратное уравнение .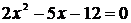

Решение:

.

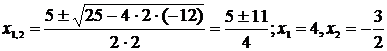Теорема 2. Если обе части уравнения 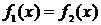, заданного на множестве Х, умножить на выражение 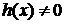, имеющее смысл для всех допустимых значений переменной, то получим уравнение, равносильное данному.

Обозначается: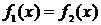

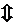
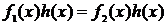
Эта теорема также применяется для решения линейных уравнений. Например, при решении уравнения 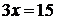(1) достаточно обе части уравнения умножить на число 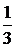; 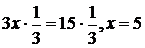.В курсе математики начальной школы уравнение (1) тоже решается на основе зависимости между компонентами действий: в уравнении (1) число 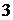- известный сомножитель, неизвестный сомножитель, 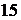-произведение; тогда для вычисления неизвестного сомножителя достаточно произведение 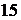разделить на известный сомножитель: .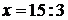