Общий признак делимости Б. Паскаля (1623 – 1662гг.).

Частные признаки делимости чисел в множестве N.

Делители чисел в множестве N.

Общие делители чисел в множестве N.

Общие кратные чисел в множестве N.

1. Отношение делимости чисел в N 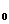и его свойства

Выше мы рассмотрели множество натуральных чисел N, операции с натуральными числами и их свойства. Однако, практика вычислений уже в начальном образовании показывает, что в различных ситуациях производить расчеты без использования числа 0 невозможно. Например, при вычитании равных чисел получаем «ничего». Для разрешения этой ситуации уже в начальных классах вводится в практику число «0», которое в приложении к теории множеств характеризует пустое множество. При дальнейшем изучении математики «0» становится полноправным числом изучаемого множества чисел. Поэтому множество N (натуральных чисел) превращается в расширенное множество N 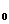, которое в дальнейшем будем называть множеством целых неотрицательных чисел.

Пусть имеем два целых неотрицательных числа a,b, кратко записывается: .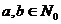

Опр.1. Число 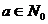называется делящимся на число 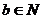с остатком, если существуют два таких числа 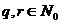, что выполняется равенство:

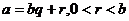. a - делимое, b – делитель, q – неполное частное, r – остаток.

Например:

1) а=47, b=6, тогда 47=6*7+5, q=7, r=5;

2) а=24, b=4, тогда 24=4*6+0, q=6, r=0;

3) а=35, b=64, тогда 35=64*0+35, q=0, r=35;

Если r=0, то a=bq, а – делимое, b – делитель, q – частное. В этом случае говорят, что «а» делится на «b», обозначается .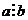

Замечание:Если в множестве 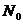рассматривается операция деления (вычисление частного или неполного частного), то говорят, что в 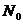задано отношение делимости.

Отношение делимости в 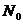обладает рядом свойств.

1. 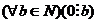- число «0» делится на любое натуральное число;

2. 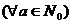: «а» не делится на 0 – любое целое неотрицательное число не делится на ноль;

3. 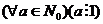- любое целое неотрицательное число делится на единицу;

4. 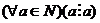- любое натуральное число делится само на себя;

5. 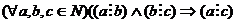- свойство транзитивности отношения делимости в N;

Общий признак делимости Б. Паскаля (1623 – 1662гг.)

Очевидно, ответ на вопрос о том, делится ли данное натуральное число «а» на натуральное число «b» может быть получен путем непосредственного деления «а» на «b». Однако, при больших числах этот процесс может быть продолжительным. Французский математик Б. Паскаль сформулировал признак, применимый к любой паре натуральных чисел и дающий возможность определить, делится ли заданное число «а» на другое данное число «b».

Признак делимости.

1. Выберем два числа: 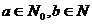, разложим число «а» по основаниям системы счисления – числа 10: 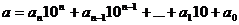(1) и будем искать условие, при котором .

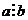1) Разделим на число «b» каждую из разрядных единиц числа «а»: :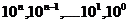

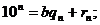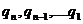- - неполные частные;

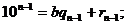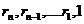- - остатки от деления степеней 10 на число «b».

………………..

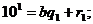
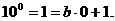
2) Подставим результаты деления в соотношение (1):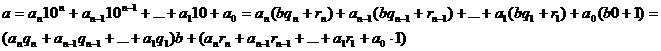

3) Обозначим S= 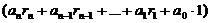- это сумма произведений чисел, обозначаемых цифрами 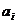числа «а», на остатки от деления соответствующих степеней 10 на число «b».

4) 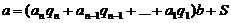, число 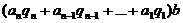делится на число «b», поэтому «а» разделится на число «b», если на «b» разделится число «S».