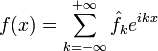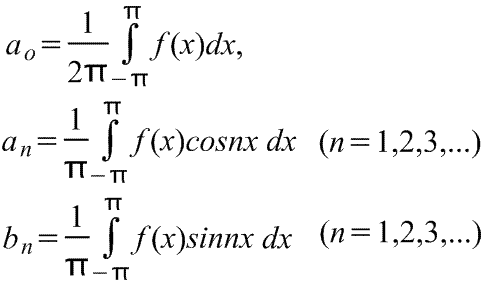Предел и непрерывность функции двух переменных

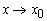Определение 1.Число А называется пределом функции в точке (или при и 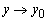), если для любого сколь угодно малого положительного числа 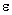найдется положительное число 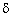такое, что для всех точек 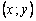, отстоящих от точки 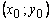на расстояние, меньшее чем 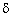, выполняется неравенство

.

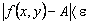Обозначается предел .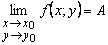

Определение 2.Функция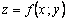
называется непрерывной в точке 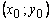, если предел функции в этой точке существует и .

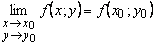Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва.

На функции нескольких переменных переносятся все свойства и методы теории пределов функции одной переменной.

2)Случайная величина — одно из основных понятий теории вероятностей. Случайная величина — этоизмеримая функция, заданная на каком-либо вероятностном пространстве

Дискретной называется случайная величина, которая при испытаниях может принимать одно из изолированных значений, количество которых конечно. К ним относятся величины из первой группы.
Непрерывной называют случайную величину, которая в пределах ее изменения может принимать любые значения , которые могут быть конечными или бесконечными . К ним относятся величины из второй группы.

Билет №6

1)Возведение в степень — бинарная операция, первоначально происходящая из многократного умножения натурального числа на самого себя. Обозначение: 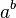называетсястепенью с основанием 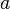и показателем .

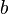Формула Муавра для комплексных чисел 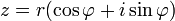утверждает, что

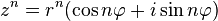
для любого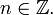

Формула названа по имени установившего её в 1707 году математика И. Муавра, друга великого И. Ньютона; современный вид формуле придал Л. Эйлер.

Доказательство [править]

Формула Муавра сразу следует из формулы Эйлера 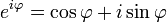и тождества для экспонент 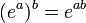, где b — целое число.^[1]

Применение [править]

Аналогичная формула применима также и при вычислении корней n-ой степени из ненулевого комплексного числа:

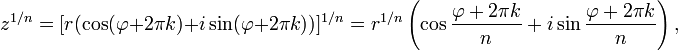
где k = 0, 1, …, n—1.

Вероятность гипотез

Вероятность гипотез.

Пусть событие А может наступить при условии появления одного из несовместных событий В1,В2,?Вn, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности:

Р(А) = Р(В1)?РВ1(А) + Р(В2) ?РВ2(А)+ ? +Р(Вn) ?РВn(А)

Формула Байеса:

,

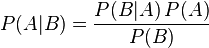где

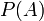— априорная вероятность гипотезы A (смысл такой терминологии см. ниже);

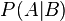— вероятность гипотезы A при наступлении события B (апостериорная вероятность);

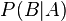— вероятность наступления события B при истинности гипотезы A;

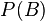— полная вероятность наступления события B.

Пример:

Пример расчёта

Пусть вероятность брака у первого рабочего 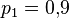, у второго рабочего — 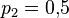, а у третьего — 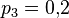. Первый изготовил 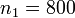деталей, второй — 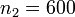деталей, а третий — 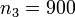деталей. Начальник цеха берёт случайную деталь, и она оказывается бракованной. Спрашивается, с какой вероятностью эту деталь изготовил третий рабочий?

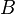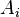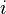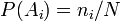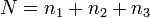Cобытие — брак детали, событие — деталь произвёл рабочий . Тогда , где , а 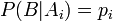. По формуле полной вероятности

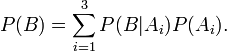
По формуле Байеса получим:

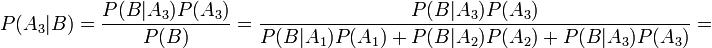
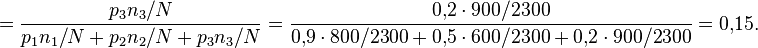
Билет №12

1. Тригонометрический ряд Фурье — представление произвольной функции 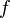с периодом 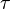в виде ряда

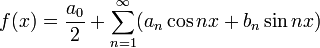или используя комплексную запись, в виде ряда:

коэффициентыao,an и bn называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a1cosx+b1sinx) называется первой или основной гармоникой,

Ряд Фурье периодических функций с периодом 2π.

Ряд Фурье

Стандартная (=обычная) запись через сумму sinx и cosx

f(x)=ao+ a1cosx+a2cos2x+a3cos3x+...+b1sinx+b2sin2x+b3sin3x+...,

где ao, a1,a2,...,b1,b2,.. - действительные константы, т.е.

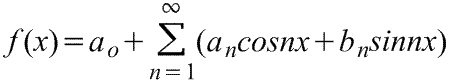
2.Противоположные события.
Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через A, то другое принято обозначать

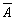
Теорема. Сумма вероятностей противоположных событий равна единице:

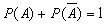
Примеры:

Пример 1. Попадание и промах при выстреле по цели — противоположные события. Если А — попадание, то противоположное событие — промах.

Пример 2. Из ящика наудачу взята деталь. События «появилась стандартная деталь» и «появилась нестандартная деталь» — противоположные

Вероятность противоположного события, очевидно, равна 10 / 21, что и утверждалось выше. [1]

Вычислим вероятность противоположного события А. Событие состоит в том, что выбранный номер не содержит ни одной из трех данных цифр. [2]

Сумма вероятностей противоположных событий равна единице. [3]

При этом вероятность противоположного события А будет больше, чем 1-а, то есть будет так же близка к единице, как вероятность события А близка к нулю

Билет №9

1. Полигоном частот называют ломанную, отрезки которой соединяют точки (x₁; n₁), (x₂; n₂), ..., (x_k; n_k). Для построения полигона частот на оси абсцисс откладывают варианты x_i, а на оси ординат - соответствующие им частоты n_i. Точки ( x_i; n_i) соединяют отрезками прямых и получают полигон частот

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению n_i / h (плотность частоты).

2. События А и В называются независимыми, если Р(АВ) = Р(А) Р(В). Несколько событий А, В, С,… называются независимыми, если вероятность их совместного осуществления равна произведению вероятностей осуществления каждого из них в отдельности: Р(АВС…) = Р(А)Р(В)Р(С)…

Иногда соотношение Р(АВ) = Р(А) Р(В|A) = P(B)P(A|B), справедливое при P(A)P(B) > 0,называют также теоремой умножения вероятностей

Билет №11

1) Случайную величину Х называют непрерывной (непрерывно распределенной) величиной, если существует такая неотрицательная функция p(t), определенная на всей числовой оси, что для всех х функция распределения случайной величины F(x) равна:

.

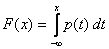
При этом функция p(t) называется плотностью распределения вероятностей непрерывной случайной величины.

Если такой функции p(t) не существует, то Х не является непрерывно распределенной случайной величиной.

Таким образом, зная плотность распределения, по формуле (6.7) можно легко найти функцию распределения F(x). И, наоборот, по известной функции распределения можно восстановить плотность распределения:

.

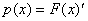
Свойства плотности распределения вероятностей

непрерывной случайной величины:

1. Плотность распределения – неотрицательная функция:

p(t)³0.

Геометрически это означает, что график плотности распределения расположен либо выше оси Ох, либо на этой оси.

2. 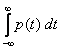=1.

Учитывая, что F(+¥)=1, получаем: 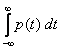=1. Т.е. площадь между графиком плотности распределения вероятностей и осью абсцисс равна единице.

Эти два свойства являются характеристическими для плотности распределения вероятностей. Доказывается и обратное утверждение:

2)

Суммой событий А и В называется третье событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.

Произведением событий А и В называется третье событие АВ, которое наступает тогда и только тогда, когда оба события: А и В.

Понятия суммы и произведения двух событий очевидным образом переносятся на случай любого множества событий.

Событием, противоположным событию А, называется событие , которое наступает тогда и только тогда, когда не наступает событие А.