Разложение в ряд Фурье по косинусам.

Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.е. не содержит членов с синусами) и может

включать постоянный член. Следовательно, 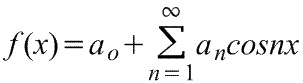где коэффициенты ряда Фурье,

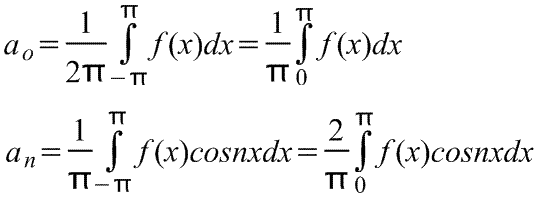
Разложение в ряд Фурье по синусам.

Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).

Следовательно,

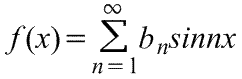где коэффициенты ряда Фурье,

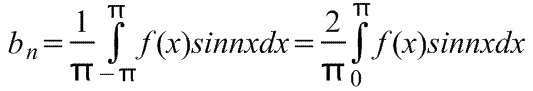
Четные и нечетные функции.

Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х² и у=cosx.

Говорят, что функция y=f(x) нечетная,если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.

14.2. Геометрическая вероятность. Примеры.Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω: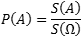

Пример 1. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения относительно большого круга. Р е ш е н и е. Площадь кольца (фигуры g) S_g = p (10² — 5²) = 75p. Площадь большого круга (фигуры G)S_G = p10² = 100p.Искомая вероятностьР = 75p / (100p) = 0,75.

Пример 2. В сигнализатор поступают сигналы от двух устройств, причем поступление каждого из сигналов равновозможно в любой момент промежутка времени длительностью Т. Моменты поступления сигналов независимы один от другого.Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше t (t < T). Найти вероятность того, что сигнализатор сработает за время T, если каждое из устройств пошлет по одному сигналу.Р е ш е н и е. Обозначим моменты поступления сигналов первого и второго устройств соответственно через х и у. В силу условия задачи должны выполняться двойные неравенства: 0 <= x <= Т, 0 <= y <= Т. Введем в рассмотрение прямоугольную систему координат хОу. В этой системе двойным неравенствам удовлетворяют координаты любой точки квадрата ОТ AT. Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют все возможные значения моментов поступления сигналов.Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше t, т. е. если
у — х < t при у > х и х — у < t при х > у, или, что то же,y< x + t при у > х, (*)y > х - t при y < х. (**)Неравенство (*) выполняется для тех точек фигуры G, которые лежат выше прямой у = х и ниже прямой y = x + t, неравенство (**) имеет место для точек, расположенных ниже прямой у = х и выше прямой у = х - t.Все точки, координаты которых удовлетворяют неравенствам (*) и (**), принадлежат заштрихованному шестиугольнику. Таким образом, этот шестиугольник можно рассматривать как фигуру g, координаты точек которой являются благоприятствующими моментами времени х и у. Искомая вероятность Р = Пл.g / Пл.G = (Т² — (Т — t)²) / T² = (t (2T — t)) / T².

Билет №4

1) Функция комплексного переменного. Это понятие — обобщение предыдущего варианта: 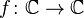.Такими функциями занимается отдельная область математического анализа — теория функций комплексного переменного, или комплексный анализ.Функция также может быть представлена в виде

,

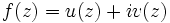однако имеется более глубокая связь между u и v. Например, для того, чтобы функция 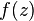была дифференцируема, должны выполняться условия Коши — Римана:

;

.

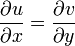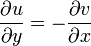Определение 1: Комплексным числом z называется пара действительных чисел (x,y), такая что z = x + i*y. x является действительной частью комплексного числа z и обозначается x = Re(z), а y - мнимая часть комплексного числа z и обозначается y = Im(z), i - мнимая единица : i*i = - 1, т.е. мнимая единица в квадрате равна минус единице.