Метрические задачи. Две главные метрические задачи.

Метрическиминазываются задачи, в которых необходимо определить значения геометрических величин – длин отрезков, размеры углов расстояние между геометрическими фигурами, площади, объемы, а также задачи на построение геометрических фигур по заданным метрическим характеристикам.

1. Группа задач, включающих в себя определение расстояний от точки до другой точки; от точки до прямой; от точки до плоскости; от точки до поверхности; от прямой до другой прямой; от прямой до плоскости; от плоскости до плоскости. Причем расстояние от прямой до плоскости и между плоскостями измеряется в тех случаях, когда они параллельны.

2. Группа задач, связанная с определением истинной величины плоской фигуры и части поверхности (развертки).

27. Способы определения расстояния между двумя точками.

Определение расстояния от точки до плоскости.

Для определения расстояния от точки до плоскости необходимо из точки опустить перпендикуляр на плоскость. Известно, что прямая перпендикулярна плоскости, если она перпендикулярна любым двум пересекающимся прямым, принадлежащим плоскости. При этом перпендикуляр может не проходить через точку пересечения прямых, а скрещиваться с ними.

Сечения. Классификация сечений.

Сечение, это воображаемый срез части предмета, образованный пересечением его с плоскостью. Профиль сечения указывается на чертеже с целью детального отображения геометрических особенностей и размеров отдельного участка детали.

Сечения подразделяются на виды отображения. К одному из таких подразделов относится, наложенное сечение, которое непосредственно располагается на изображении исходного предмета.

Вынесенное симметричное сечение ещё один способ визуализации среза предмета, который в виду своей практичности, является более предпочтительным. Такой вид зрительного воспроизведения может компоноваться в непосредственной близости от основного изображения, причём ось симметрии должна совпадать с местоположением секущей плоскости и пересекать внешнее очертание предмета.

Разрезы. Классификация разрезов.

Разрез - мысленное рассечение предмета одной или несколькими плоскостями. На разрезе показываются также и те детали и их части, которые расположены за секущей плоскостью.

1. В зависимости от числа секущих плоскостей разрезы делятся на:

· Простой разрез — для формирования используется одна плоскость. Можно не обозначать, если изображение разреза находится на месте основного вида, на одном листе с главным видом, не отделено от главного вида другими изображениями.

· Сложный разрез — для формирования используются две и больше секущих плоскостей. Обозначается всегда.

· Ломаный разрез — для формирования используются две (бо́льшее количество используется редко) пересекающиеся плоскости.

· Ступенчатый разрез — для формирования используются две и более параллельные плоскости.

2. В зависимости от положения плоскости относительно горизонтальной плоскости проекции разрезы разделяются на:

· Горизонтальные— секущая плоскость параллельна горизонтальной плоскости проекции.

· Вертикальные— секущая плоскость перпендикулярна к горизонтальной плоскости проекции.

· Наклонные— секущая плоскость составляет с горизонтальной плоскостью угол, отличный от прямого.

3. В зависимости от положения секущей плоскости относительно основных измерений предмета различают разрезы:

· Продольные — секущая плоскость направлена вдоль длины или высоты предмета.

· Поперечные— секущая плоскость перпендикулярна к длине или высоте предмета.

4. В зависимости от полноты изображения разрезы бывают:

· Полные— секущая плоскость пересекает весь предмет и изображение внутреннего его строения показывается по всему сечению.

· Местные— секущая плоскость пересекает только ту часть предмета, в которой требуется показать его внутреннюю форму. Границы местного разреза показываются тонкой сплошной волнистой линией. Местные разрезы не обозначают.

Правила нанесения размеров.

Величину изображённой детали можно определять только по размерным числам. Их наносят над размерны­ми линиями возможно ближе к их середине (рис. 4).

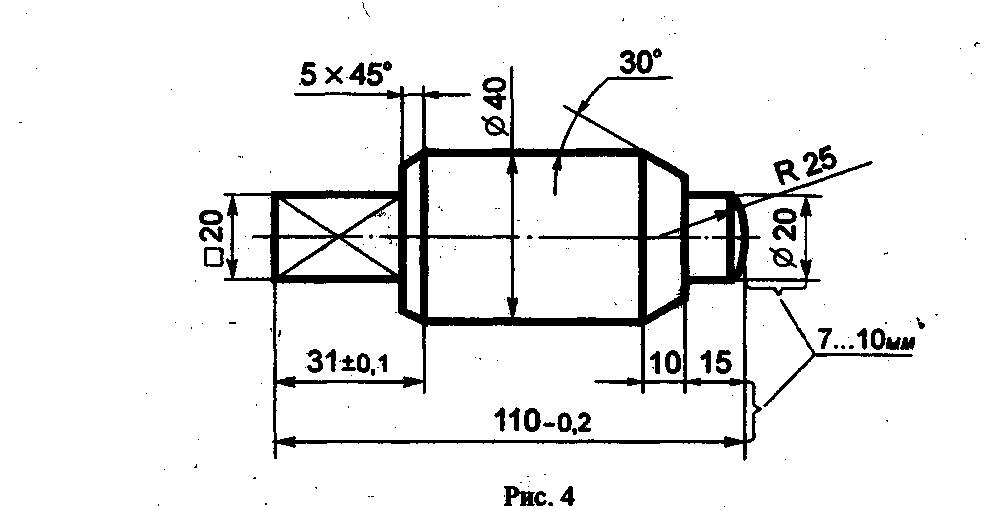
Размерные линии 'Ограничивают стрелками, кото­рые остриём должны касаться выносных линий (размеры 110, 30, 15, 0 20 и другие на рис. 4), линий контура (размер 040) или осевых линий.

Размерную линию следует проводить параллельно отрезку, размер которого указывают по возможности вне контура изображения. Расстояние между параллельными размерными линиями и от размерной линии до парал­лельной ей линии контура берут от 7 до 10 мм.

Нельзя допускать, чтобы размерные линии пересе­кались с выносными или являлись продолжением линий контура, осевых, центровых и выносных. Запрещается использовать линии контура, осевые, центровые и вы­носные в качестве размерных.

Чтобы размерные линии не пересекались с вынос­ными, меньший размер наносят ближе к изображению, а больший - дальше (размеры 15, 30 и размер 110 на рис. 4).

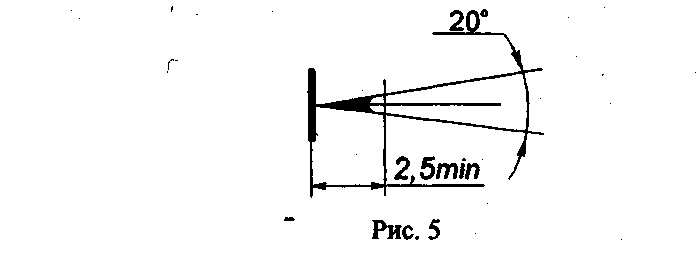
Форма стрелки показана на рис. 5. Размер стрелок следует выдерживать приблизительно одинаковым на всём чертеже.

Каждый размер на чертеже указывают только один раз.

Размерные числа линейных размеров наносят в со­ответствии с положением размерных линий, как показа­но на рис. 6. Если размерная линия вертикальная, то размерное число ставят справа (рис. 6а). На наклонных размерных линиях цифры пишут так, чтобы они оказа­лись в удобном для чтения положении, если дать раз­мерной линии "упасть" в горизонтальное положение, как это указано стрелками на рис. 6 а, б, в.

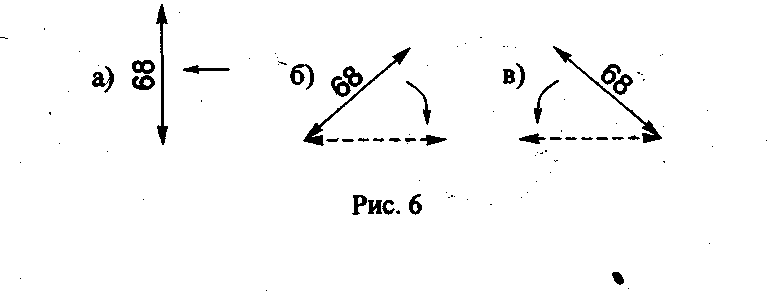
Линейные размеры на машиностроительных чер­тежах указывают в миллиметрах; если размеры нанесены у изображений, то единицы измерений (мм) не простав­ляют (см. рис.4).

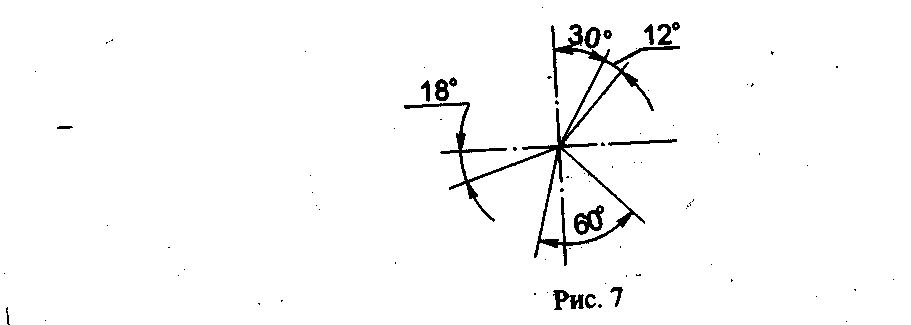
Угловые размеры наносят, как показано на рис. 7. Их указывают в градусах (°), минутах (') и секундах ("), проставляя единицы измерения, например, размер 30° на рис. 7. Размерную линию при этом проводят в виде дуги окружности с центром в вершине угла.

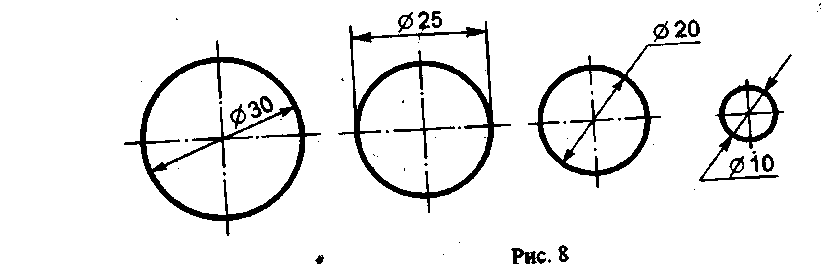
Для обозначения диаметра перед размерным чис­лом во всех случаях наносят знак - кружок, перечеркнутый прямой линией под углом 75°. Применение и по­строение этого знака показано на рис. 8.

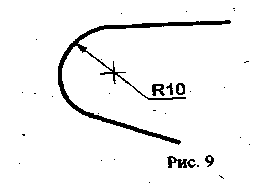Для обозначения радиуса перед размерным числом всегда наносят знак R - латинская прописная буква (см. рис. 4). Стрелку наносят с одной стороны (см. рис. 9)

Если деталь имеет не­сколько одинаковых отвер­стий или других элементов (кроме скруглений), то нано­сится размер одного из них, а количество отверстий или других элементов указывают перед размерным числом, на­пример 3 отв. 16 (рис. 10а).

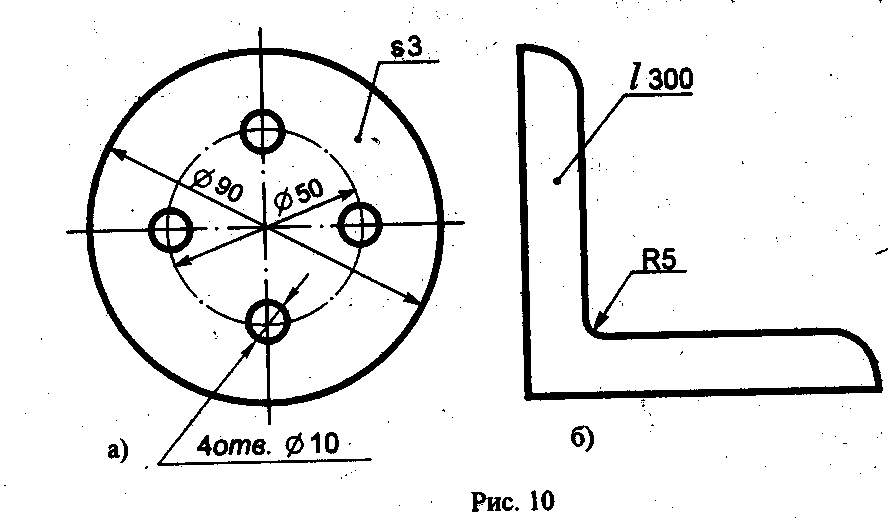
Размеры толщины или длины детали, форма которой задана одним видом, наносят, как показано на рис. 10. Пе­ред числом, указывающим толщину детали, наносят бук­ву S, а перед числом, указывающим длину детали, - бук­ву L