Образцы вопросов к итоговому контролю знаний
ОБРАЗЦЫ ВОПРОСОВ К ИТОГОВОМУ КОНТРОЛЮ ЗНАНИЙ
ПО ВЫСШЕЙ МАТЕМАТИКЕ
ДЛЯ СТУДЕНТОВ ЛЕЧЕБНОГО, ПЕДИАТРИЧЕСКОГО И МЕДИКО-ПРОФИЛАКТИЧЕСКОГО ФАКУЛЬТЕТОВ
Укажите правильный ответ
1. Функцией 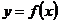 называется зависимость, при которой каждому значению переменной x соответствует:
называется зависимость, при которой каждому значению переменной x соответствует:
1) Несколько значений y
2) Одно значение y
3) Не менее одного значения y
4) Не более одного значения y
Вставьте пропущенное слово
2. Областью определения функции 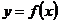 называется совокупность всех значений независимой переменной, при которых функция имеет смысл.
называется совокупность всех значений независимой переменной, при которых функция имеет смысл.
Укажите правильные ответы
3. Укажите показательные функции
1) y = ax;
2) y = xa;
3) y = ex;
4) y = ln x;
Укажите правильный ответ
4. Область определения функции 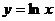 есть:
есть:
1) [ 0; 1 ];
2) ( - ∞; + ∞);
3) ( 0; +∞);
4) (- ∞; 0) 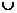 ( 0; + ∞)
( 0; + ∞)
Укажите правильный ответ
5. Область определения функции 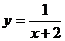 есть:
есть:
1) (- ∞; 2)  (2; + ∞);
(2; + ∞);
2) ( - ∞; + ∞);
3) (- ∞; -2)  ( -2; + ∞);
( -2; + ∞);
4) (- ∞; -2)  (-2; 2)
(-2; 2) 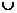 (2; + ∞)
(2; + ∞)
Укажите правильный ответ
6. График функции 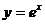 изображен на рисунке:
изображен на рисунке:
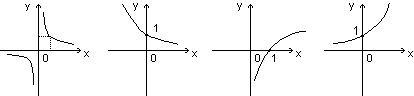
рис.1 рис. 2 рис.3 рис. 4
Укажите правильный ответ
7. На числовой прямой дана точка x=5,1. Тогда «ε-окрестностью» может являться интервал
1) (4,9; 5,5);
2) ( 4,9; 5,3);
3) (5,1; 5,4);
4) (4,8; 5,1).
Укажите правильный ответ
8. Число точек разрыва функции 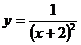 равно:
равно:
1) 4;
2) 1;
3) 3;
4) 0.
Укажите правильный ответ
9. Функция называется бесконечно малой, если:
1) 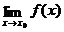 =x0
=x0
2) 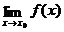 = ¥
= ¥
3) 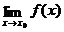 =0
=0
4) 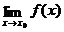 =f(x)
=f(x)
Укажите правильный ответ
10. Предел 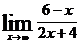 равен:
равен:
1) -1/4;
2) 3/2;
3) ∞
4) -1/2
Укажите правильный ответ
11. Предел 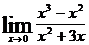 равен:
равен:
1) 1;
2) 0;
3) ∞
4) 1/3
Укажите правильный ответ
12. Приращением функции 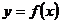 в т. х0 при приращении аргумента Δх называется:
в т. х0 при приращении аргумента Δх называется:
1) 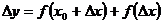 ;
;
2) 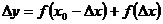 ;
;
3) 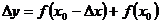 ;
;
4) 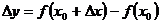
Укажите правильный ответ
13. Производной функции 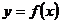 в точке х называется:
в точке х называется:
1) 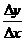 ;
;
2) 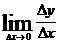 ;
;
3) 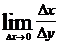 ;
;
4) 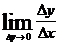
Укажите правильный ответ
14. График функции y=f(x) изображен на рисунке.
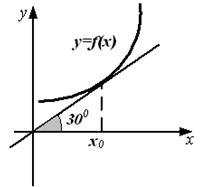
Значение производной это функции в точке х0 равно:
1) 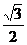 ;
;
2) 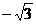 ;
;
3) 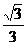 ;
;
4) 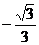 .
.
Укажите правильный ответ
15. На рисунке изображен график производной функции y=f(x) заданной на отрезке [-1;8].
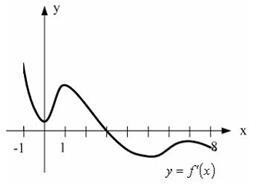
Тогда точкой максимума этой функции является:
1) 1; 2) 3; 3) 8; 4) 7.
Укажите соответствия
16. Производные основных функций – см. таблицу
| Функция | Производная |
| 1. y = ах | 1. 0 |
| 2. y = C, C - const | 2. ex |
| 3. y = ex | 3. nxn-1 |
| 4. y = xn | 4. 1 |
| 5. ax ln x | |
6. 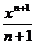 |
Укажите правильный ответ
17. Производная функции 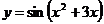 равна:
равна:
1) 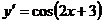 ;
;
2) 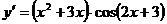 ;
;
3) 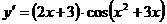 ;
;
4) 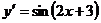
Укажите правильный ответ
18. В соответствии с определением дифференциалом функции называется:
1) Приращение функции;
2) Главная часть приращения функции, линейная относительно приращения аргумента;
3) Произведение производной функции на дифференциал аргумента;
4) Тангенс угла наклона касательной к графику функции
Укажите правильный ответ
19. Дифференциал функции вычисляется по формуле:
1) dy = y'Dx+a(x)Dx
2) dy = y'dx
3) dy = y'Dx
4) dy = a(x)Dx
Укажите правильный ответ
20. Дифференциал функции 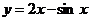 равен:
равен:
1) 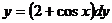 ;
;
2) 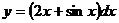 ;
;
3) 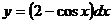 ;
;
4) 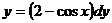
Укажите правильный ответ
21. Функция 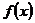 называется строго возрастающей на ( а, b), если для любых двух точек х1 и х2 из этого интервала и из х1 <х2 следует:
называется строго возрастающей на ( а, b), если для любых двух точек х1 и х2 из этого интервала и из х1 <х2 следует:
1) 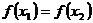 ;
;
2) 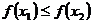 ;
;
3) 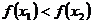 ;
;
4) 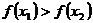
Вставьте пропущенное слово
22. Точки минимума и точки максимума называются экстремумами функции.
Вставьте необходимое слово и неравенство
23. Точка х0 называется точкой минимума функции f(х), если существует окрестность точки х0, такая, что для любого х из этой окрестности f(x)>f(x0). (по определению минимума функции)
Вставьте пропущенное слово
Достаточное условие монотонности функции:
24. Если 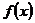 имеет в каждой точке (a,b)
имеет в каждой точке (a,b) 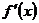 >0 , то функция возрастает на (a,b).
>0 , то функция возрастает на (a,b).
Продолжите фразу
25. такого вопроса не будет.
Вставьте пропущенное слово
26. Полный дифференциал функции нескольких переменных равен сумме частных дифференциалов этой функции.
Вставьте пропущенное слово
27. Чтобы найти частную производную функции 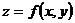 по переменной y необходимо рассматривать переменную y как переменную, а х как постоянную.
по переменной y необходимо рассматривать переменную y как переменную, а х как постоянную.
Укажите правильный ответ
28. Частный дифференциал функции 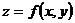 по переменной х вычисляется по формуле:
по переменной х вычисляется по формуле:
1) 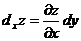
2) 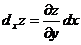
3) 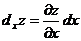
4) 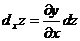
Укажите правильный ответ
29. Частная производная функции 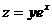 по переменной х равна:
по переменной х равна:
1) 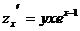
2) 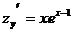
3) 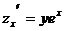
4) 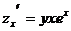
Укажите правильный ответ
30. Полный дифференциал функции 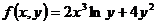 равен:
равен:
1) 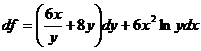 ;
;
2) 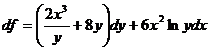 ;
;
3) 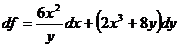 ;
;
4) 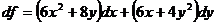 .
.
Продолжите фразу
31. Функция F(х) называется первообразной функции f(х), если они связаны равенством F’(х)= f(х).
Укажите правильный ответ
32. Множество первообразных функции 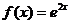 имеет вид:
имеет вид:
1) 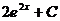
2) 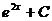
3) 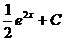
4) 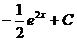
Укажите соответствия
34. Основные формулы интегрирования – см.таблицу
| Подынтегральная функция | Первообразная |
| 1. 1 | a) nxn-1+C |
| 2. хn | b) ex+C |
| 3. ex | c) х+С |
4.  | d) 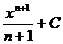 |
e)  +C +C | |
f) 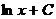 |
Укажите соответствия
35. Основные свойства неопределенного интеграла – см. свойства в лекциях
| Левая часть равенства | Правая часть равенства |
| 1. [òf(x)dx]’ | а) F(x)+C |
| 2. dòf(x)dx | б) f(x)dx |
| 3. òdF(x) | в) f(x) |
| г) f(x)+C |
Укажите правильный ответ
36. При вычислении интеграла 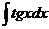 вводим новую переменную:
вводим новую переменную:
1) t = sin x
2) t = cos x
3) t = tgx
4) x = a
Укажите правильный ответ
37. За новую переменную при вычислении неопределенного интеграла 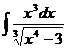 обозначают выражение
обозначают выражение 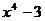 :
:
Укажите правильный ответ
38. Формула Ньютона-Лейбница:
1) 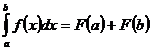 ;
;
2) 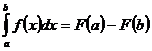 ;
;
3) 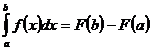
4) 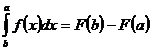 ;
;
Укажите правильный ответ
40. Если подынтегральная функция сохраняет свой знак на промежутке интегрирования, то определенный интеграл представляет собой число того же знака, что и функция.
Укажите правильный ответ
41. Площадь криволинейной трапеции D
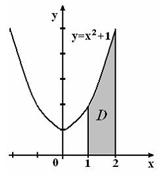
равна:
1) 7/3;
2) 10/3;
3) 14/3;
4) 8/3.
Укажите правильный ответ
42. Формула Ньютона-Лейбница та же:
Укажите правильный ответ
43. Определенный интеграл 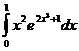 равен не будет:
равен не будет:
Вставьте пропущенное слово
44. Если искомая функция y = f(x) есть функция одного аргумента, то дифференциальное уравнение называют обыкновенным.
Укажите правильный ответ
45. Общим решением дифференциального уравнения порядка k называется функция:
1) 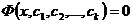 , где
, где 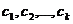 - произвольные постоянные;
- произвольные постоянные;
2) 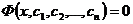 , где
, где 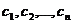 - произвольные постоянные;
- произвольные постоянные;
3) 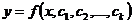 , где
, где 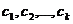 - произвольные постоянные;
- произвольные постоянные;
4) 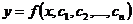 , где
, где 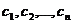 - произвольные постоянные.
- произвольные постоянные.
Укажите правильный ответ
47. Общим интегралом дифференциального уравнения с разделяющимися переменными 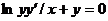 является функция:
является функция:
1) 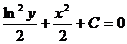 ;
;
2) 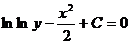 ;
;
3) 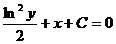 ;
;
4) 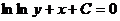
Укажите правильный ответ
48. Общее решение дифференциального уравнения 2 порядка с постоянными коэффициентами 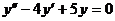 есть функция:
есть функция:
1) 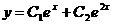 ;
;
2) 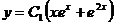
3) 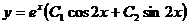 ;
;
4)  ;
;
Вставьте пропущенное слово
49. Линейным неоднородным дифференциальным уравнением 2 порядка с постоянными коэффициентами y’’+py’+qy=0.
Укажите соответствия
50. Вид общего решения дифференциального уравнения второго порядка с постоянными коэффициентами 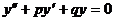 в зависимости от вида корней характеристического уравнения. – см. лекции
в зависимости от вида корней характеристического уравнения. – см. лекции
| Вид корней характеристического уравнения | Общее решение дифференциального уравнения |
| 1. k1≠k2 – действительные числа | a) 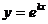 |
| 2. k1=k2 – действительные числа | b) 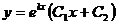 |
| 3. k1≠k2 – комплексные числа | c) 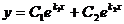 |
d) 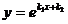 | |
e) 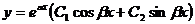 | |
f) 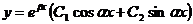 |
Укажите правильный ответ
51. Закон поглощения света Бугера-Ламберта-Бера выводится из дифференциального уравнения:
1) 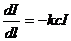 , где I – интенсивность света, с – концентрация вещества, k – коэффициент поглощения;
, где I – интенсивность света, с – концентрация вещества, k – коэффициент поглощения;
2) 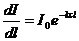 , где I – интенсивность света, с – концентрация вещества, k – коэффициент поглощения;
, где I – интенсивность света, с – концентрация вещества, k – коэффициент поглощения;
3) 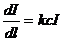 , где I – интенсивность света, с – концентрация вещества, k – коэффициент поглощения;
, где I – интенсивность света, с – концентрация вещества, k – коэффициент поглощения;
4) 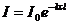 , где N – число распавшихся ядер, N0 – начальное число ядер, t – время распада, λ – постоянная распада
, где N – число распавшихся ядер, N0 – начальное число ядер, t – время распада, λ – постоянная распада
Укажите правильный ответ
52. Закон радиоактивного распада выводится из дифференциального уравнения:
1) 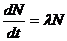 , где N – число нераспавшихся ядер, t – время распада, λ – постоянная распада;
, где N – число нераспавшихся ядер, t – время распада, λ – постоянная распада;
2) 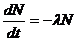 , где N – число нераспавшихся ядер, t – время распада, λ – постоянная распада;
, где N – число нераспавшихся ядер, t – время распада, λ – постоянная распада;
3) 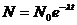 , где N – число распавшихся ядер, N0 – начальное число ядер, t – время распада, λ – постоянная распада
, где N – число распавшихся ядер, N0 – начальное число ядер, t – время распада, λ – постоянная распада
Укажите правильный ответ.
53. По формуле перестановок из n элементов данного множества рассчитывается по формуле:
1) 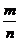 .
.
2)  .
.
3) 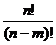 .
.
4) 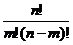
Укажите правильный ответ.
54. По формуле 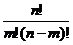 рассчитывается
рассчитывается
1) Число размещений из n элементов по m.
2) Число размещений из m элементов по n.
3) Число сочетаний из n элементов по m.
4) Число сочетаний из m элементов по n
Укажите правильный ответ.
55. Количество перестановок из 5 элементов равно:
1) 5
2) 120
3) 20
4) 25.
Впишите пропущенное слово.
56. Осуществление некоторого определенного комплекса условий, который может быть воспроизведен сколь угодное число раз называется испытанием.
Впишите пропущенное слово.
57. Любой результат или исход испытания называется событием.
Укажите соответствие
58. Классификация событий
| Событие | Характеристика |
| 5. невозможные (д) | а) в результате испытания обязательно наступают |
| 6. совместные (б) | б) появление одного из событий не исключает появление других в одном и том же испытании |
| 7. независимые (ж) | в) появление одного из событий исключает появление других в одном и том же испытании |
| г) события, из которых в результате испытания одно обязательно должно произойти | |
| д) в результате испытания никогда не наступит | |
| ж) вероятность любого из событий не зависит от осуществления остальных |
Впишите пропущенное слово.
59. Группа событий, любое из которых может осуществиться при каждом испытании, и не может осуществиться несовместное с ним, называется полной .
Впишите пропущенное слово .
60. Численная мера степени объективной возможности наступления события называется вероятностью события.
Укажите правильный ответ
62. Вероятность любого события заключается в интервале:
1) 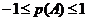
2) 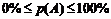
3) 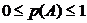
4) 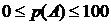
Укажите правильный ответ
63. Вероятность достоверного события равна
1) m/n
2) 0
3) самой себе
4) практически нулю
5) 1
Впишите пропущенные слова .
65. Статистической вероятностью события А называется предел отношения относительной частоты при стремлении числа наблюдений к бесконечности .
Укажите правильный ответ
66. Теорема сложения вероятностей – в тесте нет.
| Вид событий | Формула |
| 1. несовместные | а. 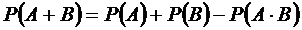 |
| 2. совместные | б. 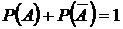 |
| 3. противоположные | в.  |
г. 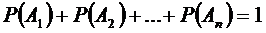 |
Укажите правильный ответ
67. Если события образуют полную группу, то сумма их вероятностей равна:
1) большей вероятности
2) 2,72
3) меньшей вероятности
4) 1
5) 0
Укажите правильный ответ
68. В ящике находится 20 шаров: 5 синих, 10 красных и 5 черных. Какова вероятность того, что при одном извлечении появится цветной шар?
1) 0,75
2) 0,5
3) 0
4) 0,05
Укажите правильный ответ
69. Студент перед зачетом умеет решать 10 задач на дифференцирование, 5 задач на интегрирование и 1 дифференциальное уравнение. Какова вероятность, что он решит первую наугад взятую задачу из билета на зачете, если всего 30 билетов:
1) ½
2) 1/30
3) 16/30
4) 1/6
Впишите пропущенное слово .
70. Если вероятность наступления события В зависит от того, наступления события А, то вероятность события В называется условной .
Укажите правильный ответ
71. В корзине 5 шаров: 3 белых, 2 черных. Какова вероятность события, состоящего в том, что при первом извлечении появился белый шар, а при втором черный.
1) 1/2
2) 3/5
3) 3/10
4) 3/2
Укажите правильный ответ
72. Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,6 и 0,3 соответственно. Тогда вероятность того, что в цель попадут оба стрелка равна?
1) 0,15
2) 0,28
3) 0,18
4) 0,9
Укажите правильный ответ
73. Если событие А наступает только при наступлении одного из полной группы событий В1,В2,…Вn, то по формуле Байеса
1) 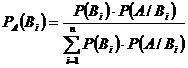
2) 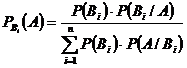
3) 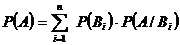
4) 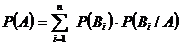
Укажите правильный ответ
74. В первой урне 4 черных и 6 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна:
1) 0,15;
2) 0,9;
3) 0,4;
4) 0,45.
Укажите правильный ответ
76. Формула Бернулли:
1) 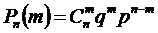
2) 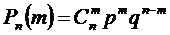
3) 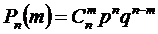
4) 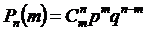
Укажите правильный ответ
77. По формуле Бернулли:
1) 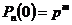 ;
;
2) 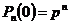 ;
;
3) 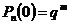 ;
;
4) 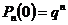 .
.
Укажите правильный ответ - не будет
78. Если вероятность взрыва в отдельном опыте равна 0,23, то вероятность одного взрыва серии из 3 опытов равна:
1) 0,15
2) 0,82
3) 0,41
4) 0,12
Впишите пропущенное слово .
79. Локальная теорема Лапласа.
Если вероятность осуществления некоторого события А в n испытаниях постоянна и отлична от 0 и 1, то вероятность 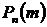 приближенно равна значению функции
приближенно равна значению функции 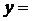 ________.
________.
Укажите правильный ответ
80. Интегральная теорема Лапласа применяется для вычисления...
1) Вероятности того, что в n независимых испытаниях, в каждом из которых вероятность осуществления события равна р (0<p<1), событие наступит m раз;
2) Вероятности того, что в n независимых испытаниях, в каждом из которых вероятность осуществления события равна р (0<p<1), событие наступит не мене k1 раз и не более k2 раза;
3) Вероятности того, что в n независимых испытаниях, в каждом из которых вероятность осуществления события равна р (0≤p≤1), событие наступит не мене k1 раз и не более k2 раза;
Укажите правильный ответ
81. Вероятность того, что дом может сгореть в течение года, равна 0,01. Застраховано 500 домов. Для вычисления вероятности того, что сгорит не более 6 домов, следует использовать:
1) Локальную формулу Муавра-Лапласа;
2) Интегральную формулу Муавра-Лапласа;
3) Формулу полной вероятности;
4) Формулу Пуассона.
Укажите правильный ответ
82. Рядом распределения дискретной случайной величины называется:
1) Соответствие между её возможными значениями и их вероятностями;
2) Запись значений случайной величины в порядке возрастания;
3) Соответствие между математическим ожиданием случайной величины и её дисперсией;
4) Соответствие между значениями случайной величины и её частотами
Впишите пропущенное слово .
83. Случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями называют дискретной.
Укажите правильный ответ
84. Многоугольник распределения – это ломаная, соединяющая точки с координатами:
1) 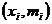
2) 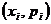
3) 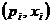
4) 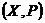
Укажите соответствие
85. Числовые характеристики дискретных случайных величин
| Характеристика | Формула |
1. 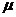 = (в) = (в) | а. 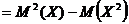 |
2. 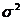 = (а,б,д) = (а,б,д) | б. 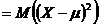 |
3. 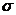 = (г) = (г) | в. 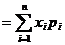 |
г. 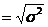 | |
д. 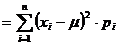 |
Укажите правильный ответ
87. Дисперсия случайной величины характеризует:
1) Среднее арифметическое значений случайной величины;
2) Условие нормировки случайной величины;
3) Положение случайной величины;
4) Степень рассеяния случайной величины около её математического ожидания;
Укажите соответствие
88. Свойства дисперсии дискретной случайной величины
1. 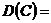 (в) (С - const) (в) (С - const) | а. 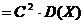 |
2. 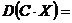 (а) (С - const) (а) (С - const) | б. 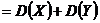 |
3. 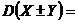 (б) (б) | в. 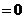 |
г. 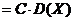 | |
| д. =1 | |
е. 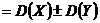 |
Укажите правильный ответ
89. Математическое ожидание дискретной случайной величины Х, имеющий закон распределения
| х | -2 | 5,5 | ||
| р | 0,15 | 0,23 | 0,34 | 0,28 |
равно:
1) 3,29
2) 11,5
3) 4,6
4) 3,8
Укажите правильный ответ
90. Вероятности значений дискретной случайной величины, распределенной по закону Пуассона, вычисляется по формуле:
1) 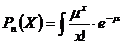 dx
dx
2) 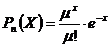
3) 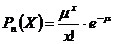
4) 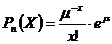 ;
;
Укажите правильный ответ
91. В формуле Пуассона параметр μ находится как:
1) qm;
2) nq;
3) np
4) mp
Впишите пропущенные слова .
92. Функцией распределения непрерывной случайной величины Х называется функция, равная вероятности того, что случайная величина приняла значение меньше х.
Укажите правильный ответ
93. Функция распределения для дискретной случайной величины, закон распределения которой представлен следующей таблицей
| х | |||||
| р | 0,1 | 0,25 | 0,3 | 0,25 | 0,1 |
Задается следующей системой:
1) 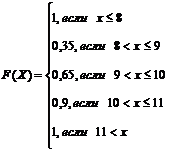 2)
2) 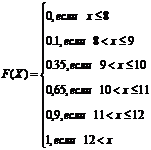 3)
3) 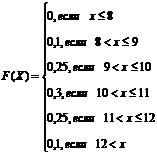
Укажите правильный ответ
94. Плотностью распределения непрерывной случайной величины Х называют функцию f(х):
1) Равную вероятности того, что случайная величина приняла значение равное заранее заданному;
2) Равная определенному интегралу её функции распределения;
3) Равную производной её плотности вероятностей;
4) Равную производной её интегральной функции;
Укажите правильный ответ
95. Условие нормировки функции плотности вероятности:
1) 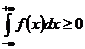
2) 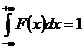
3) 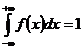
4) 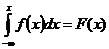
Укажите правильный ответ
96. Если задана плотность распределения непрерывной случайной величины Х 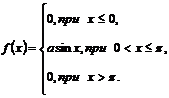 , то коэффициент а можно определить, используя следующее свойство функции плотности распределения:
, то коэффициент а можно определить, используя следующее свойство функции плотности распределения:
1) f(x) – функция неотрицательная
2) 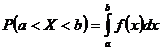
3) 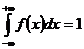
4) 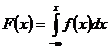
Укажите правильный ответ
97. Зная плотность распределения случайной величины, её функцию распределения находят с помощью формулы:
1) 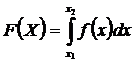 ;
;
2) 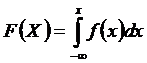 ;
;
3) 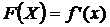 ;
;
4) 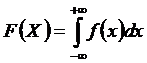
Укажите правильный ответ
98. не будет
Укажите правильный ответ
99. Математическое ожидание непрерывной случайной величины рассчитывается по формуле:
1) 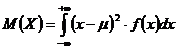
2) 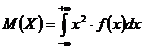 3
3
3) 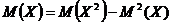
4) 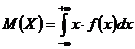
Укажите правильный ответ
100. Математическое ожидание случайной величины Х, функция плотности вероятности которой 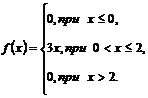 , равно:
, равно:
1) 8
2) 12
3) 0
4) 3
Укажите правильный ответ
103. Медианой непрерывной случайной величины Х называется то ее возможное значение, для которого выполняется равенство:
1) 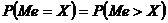
2) 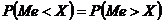
3) 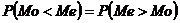
4) 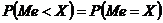
Впишите пропущенные слова .
104. Непрерывная случайная величина Х имеет равномерное распределение вероятностей на отрезке 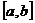 , если её плотность вероятности на отрезке
, если её плотность вероятности на отрезке 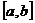 постоянна, а вне отрезка равна нулю .
постоянна, а вне отрезка равна нулю .
Укажите правильный ответ
105. График плотности распределения вероятностей непрерывной случайной величины Х, распределенной равномерно в интервале (-1;4), имеет вид:
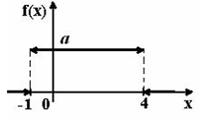 ,
,
Тогда значение а равно:
1) 1;
2) 0,33;
3) 0,25;
4) 0,2.
Укажите правильный ответ
106. Функция распределения непрерывной случайной величины Х, распределенной по равномерному закону на 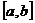 , есть
, есть
1) 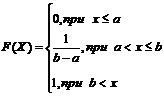 ; 2)
; 2) 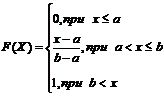 ; 3)
; 3) 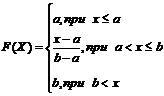
Укажите соответствия
107. Влияние изменения параметров 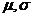 на форму и расположение кривой Гаусса
на форму и расположение кривой Гаусса
| Изменение параметра | Преобразование кривой |
1. Увеличение 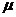 (б) (б) | а. Перемещение кривой вправо |
2. Уменьшение 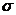 (в,д) (в,д) | б. Перемещение кривой влево |
| в. Увеличение значения максимума плотности распределения | |
| г. Уменьшение значения максимума плотности распределения | |
| д. Более резкий спад кривой | |
| е. Мене резкий спад кривой |
Укажите правильный ответ
108. Закон распределения вероятностей непрерывной случайной величины Х, называется нормальным, если плотность распределения задается функцией:
1) 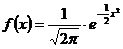
2) 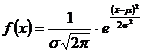
3) 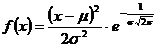
4) 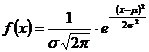
, где 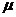 -математическое ожидание н.с.в. Х,
-математическое ожидание н.с.в. Х, 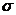 - среднее квадратическое отклонение н.с.в. Х
- среднее квадратическое отклонение н.с.в. Х
Укажите правильный ответ
109. Функция плотности распределения нормальной непрерывной случайной величины Х с математическим ожиданием 0 и дисперсией 16 имеет вид:
1) 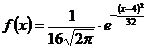
2) 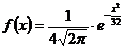
3) 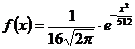
4) 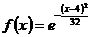
Впишите пропущенные слова .
110. Нормальный закон распределения с параметрами 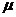 = 0 и
= 0 и 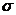 = 1 называют нормированным.
= 1 называют нормированным.
Укажите правильный ответ
111. Функция плотности распределения непрерывной случайной величины Х, распределенной по стандартному закону, задается функцией:
1) 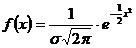
2) 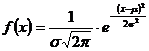
3) 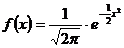
4) 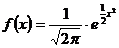
Укажите правильный ответ
112. Вероятность попадания непрерывной случайной величины Х в интервал 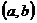 рассчитывается по формуле:
рассчитывается по формуле:
1) 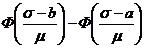
2) 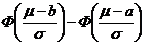
3) 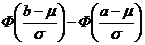
4) 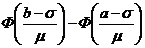
Укажите правильный ответ
113. Вероятность того, что отклонение нормально распределенной случайной величины Х от ее математического ожидания по абсолютной величине меньше заданного положительного числа рассчитывается по формуле:
1) 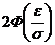
2) 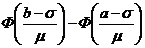
3) 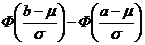
4) 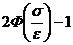
Укажите правильный ответ
114. Все возможные значения непрерывной случайной величины Х, подчиненной по нормальному закону с параметрами 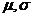 , заключены в интервале:
, заключены в интервале:
1) 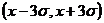
2) 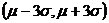
3) 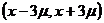
4) 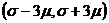
Укажите правильный ответ
115. Из генеральной совокупности извлечена выборка объема n=50, полигон частот которой имеет вид
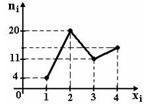
Тогда число вариант хi=4 в выборке равно:
1) 14;
2) 16 ;
3) 15;
4) 50.
Укажите правильный ответ
116. Мода вариационного ряда 1,2,2,3,4,5 равна:
1) 5;
2) 3;
3) 17;
4) 2.
Укажите правильный ответ
117. Произведены 4 измерения (без систематических ошибок) некоторой случайной величины (в мм): 5, 6, 9, 12. тогда несмещенная оценка математического ожидания равна:
1) 8,25;
2) 7;
3) 8,5;
4) 8.
Укажите правильный ответ
118. Точечная оценка математического ожидания нормального распределения равна10. тогда его интервальная оценка может иметь вид:
1) (8,4; 10);
2) ( 10; 10,9);
3) (8,6; 9,6);
4) (8,5; 11,5).
ОБРАЗЦЫ ВОПРОСОВ К ИТОГОВОМУ КОНТРОЛЮ ЗНАНИЙ
ПО ВЫСШЕЙ МАТЕМАТИКЕ
ДЛЯ СТУДЕНТОВ ЛЕЧЕБНОГО, ПЕДИАТРИЧЕСКОГО И МЕДИКО-ПРОФИЛАКТИЧЕСКОГО ФАКУЛЬТЕТОВ
Укажите правильный ответ
1. Функцией 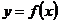 называется зависимость, при которой каждому значению переменной x соответствует:
называется зависимость, при которой каждому значению переменной x соответствует:
1) Несколько значений y
2) Одно значение y
3) Не менее одного значения y
4) Не более одного значения y
Вставьте пропущенное слово
2. Областью определения функции 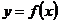 называется совокупность всех значений независимой переменной, при которых функция имеет смысл.
называется совокупность всех значений независимой переменной, при которых функция имеет смысл.
Укажите правильные ответы
3. Укажите показател<
