Физическое моделирование орудий лова

Тема Методика расчетов масштабов подобия

Геометрическое, статическое, кинематическое и динамическое подобие.При геометрическом подобии необходимо соблюдать по­стоянным лишь один масштаб линейных размеров С_l=l_M/l_H. Дополни­тельным условием (критерием) геометрического подобия является равенство всех углов (a) между соответствующими линиями на модели и натуре, т. е.

a = idem. (6.1)

Статическое подобие имеет место, если при моделировании обеспечено постоянство масштабов линейных размеров Cl и масштабов действующих сил C_R=R_M/R_HНеобходимо, чтобы внешние силы, приложенные к геометрически подобным модели и натуре, были одинаково ориентированы относительно осей координат. Условие a_M = a_H при этом также должно выполняться.

В некоторых случаях статического подобия масштабы Сl и C_R между собой не связаны и могут выбираться произвольно. Един­ственным критерием подобия является условие (6.1). Такое поло­жение имеет место при рассмотрении форм равновесия гибких сис­тем и их моделей без учета удлинения.

В других случаях статического моделирования требуется вы­полнение дополнительных условий и масштабы C_l и C_R оказыва­ются зависимыми между собой. Форма этой связи определяется исходя из природы действующих сил исоответствующих физических законов. Так, если моделируются силы плавучести или веса оснастки подбор орудий лова, то упомянутая связь имеет вид:

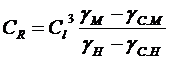(6.2)

P_H=V_H(g_H-g_C.H)

P_М=V_М(g_М- g_C.М)

где g_М — объемный вес материала деталей оснастки модели; g_H — объемный вес материала деталей оснастки натуры; g_C.М — объем­ный вес среды, в которой осуществляется моделирование; g_C.H — объемный вес натурной среды (воды).

При моделировании процесса растяжения гибкой нити крите­рием подобия является e=idem. Связь между мас­штабами C_l и C_R будет различной в зависимости от свойств ма­териала нити. Так, если растяжение нити происходит по закону Гука, то

C_R = C_l²E_M/E_H. (6.3)

Соотношения статического подобия широко используются для решения задач промышленного рыболовства. К их числу, напри­мер, относится определение элементов гибкой нити, ее натяжения и реакций в точках закрепления. В соответствии с материалами гла­вы 3 такие задачи решаются аналитически, однако в более слож­ных ситуациях, когда нагрузка распределена неравномерно по длине нити или когда требуется получить решение при перемеще­нии точек подвеса, целесообразно применить метод статического моделирования.

С этой целью гибкая нить раскрепляется на вертикальном щите. Так как растяжение нити практически отсутствует, то необ­ходимым и достаточным условием подобия является соблюдение постоянства значений двух масштабов Сs и C_R, не связанных между собой.

Результаты таких опытов могут быть использованы для опре­деления реакций в точках закрепления полоски сети, находящейся под действием сил тяжести и сопротивления. Расчетная схема к такой задаче показана на рис. 53. На основе пересчета данных опытов с гибкой нитью для схемы на рис. 53 построены графи­ки, приведенные в приложении 19 [1]. С их помощью рассчитываются горизонтальные (R₁, R₂) и вертикальные (Т₁, Т₂) составляющие реакции в точках закрепления сети в за­висимости от соотношения внешних сил (Q/R) и геометрических характеристик сети (H/S). На статическом подобии базируется метод механической имитации, представляющий собой разновидность известногометода механической аналогии.

Подобие называется кинематическим, когда сохранены постоянными зна­чения масштаба линейных размеров Cl и времени Сt. В некоторых случаях соб­людение этого условия является доста­точным, чтобы системы были кинематически подобными, и потому взаимосвязь между масштабами Cl и Ct отсутствует. Примером может служить движение двух подобных шатунно-кривошипных механизмов. В большинстве же случаев постоянство значений масштабов Cl и C_t не является дос­таточным для обеспечения подобия. Необходимо выполнение, кроме того, дополнительного условия, определенным образом связывающего эти масштабы. Форма связи зависит от физического существа яв­ления.

Если при моделировании соблюдается постоянство масштабов C_l, C_t и C_R, то та­кое подобие носит название динамического. Со­блюдение этого условия не является достаточным. При динами­ческом подобии необходимо обеспечить выполнение до­пол­нитель­ных условий, связывающих между собой указанные масштабы подобия. Форма этой связи определяется физическими условиями, характерными для моделируемого процесса

Условия подобия рыболовных орудий.Подобие для рыболов­ного орудия и его модели достигается при выполнении следую­щих требований: натурное орудие и его модель должны иметь одинаковые по форме развертки сетей; начальные и граничные условия для модельного и натурного потоков должны быть тож­дественны и могут отличаться лишь масштабами заданных вели­чин; должны соблюдаться условия геометрического подобия сетей и канатного каркаса; должны соблюдаться условия силового подо­бия.

К условиям геометрического подобия относятся:

a/l = idem; (6.4)

d/a = idem\ (6.5)

x=idem_; (6.6)

u_x = idem ; (6.7)

u_y = idem, (6.8)

где x — коэффициент укрута, характеризующий состояние поверх­ности ниток.

Условиями силового подобия рыболовных орудий являются:

Re = vd/v =idem; (6.9)

Пg*= pv²/(g*·d) = idem; (6.10)

Ne = R/(pl²v²) = idem; (6.11)

EI//pl⁴v² = idem_; (6.12)

e = idem: (6.13)

В условии (6.12) EI — изгибная жесткость канатов каркаса орудия лова (в Н·м²).

И наконец, помимо перечисленных, к числу условий подобия относится

Sh = vt/l = idem. (6.14)

Совместное выполнение условий (6.4)-(6.14) в большинстве случаев оказывается невозможным. Тогда осуществляется при­ближенное подобие с надлежащим учетом возникающих погреш­ностей— масштабного эффекта.

Критерий Рейнольдса (6.9) характеризует соотношение сил гидродинамических и сил вязкого трения частиц воды о поверх­ность сети.

Чтобы исключить технические трудности, возникающие при выполнении условия (6,9), опыты с моделями проводятся в авто­модельной (для сетного полотна) области по числу Re, где зна­чения коэффициентов сопротивления сетей слабо зависят от чис­ла Re. В этом случае несоблюдение условия (6.9) на результаты экспериментов с моделями существенно не отражается. Автомо­дельная область соответствует значениям числа Re>-600.

Условие (6.10) называется обобщенным критерием Фруда, ко­торый характеризует соотношение гидродинамических сил и сил тяжести сетного полотна в воде. Экспериментально установлено, что величина сил тяжести на форму и положение рыболовных се­тей, ниток и канатов несущественны при значениях Fr*>130.

Условие (6.11) называется критерием Ньютона, который ха­рактеризует соотношение сил, создаваемых оснасткой орудий лова, и сил гидродинамических. Поскольку силы оснастки всегда суще­ственно влияют на форму орудия, условием (6.11) пренебрегать нельзя. Для учета характеристик сетей и невыполняемых условий подобия критерий Ньютона записывают в виде

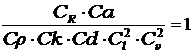(6,15)

где С_k=Схм /Схн — масштаб коэффициентов сопротивления гидро­динамических сил, зависящих от числа Re и относительной пло­щади сети F_O.

Условие (6.12) характеризует соотношение сил изгибной жест­кости канатов и сил гидродинамических. Его выполнение необхо­димо лишь в тех случаях, когда силы изгибной жесткости канатов оказывают существенное влияние на форму орудия или модели, возникающую под действием гидродинамических сил.

Условие (6.13) характеризует относительное удлинение нитей и канатов под воздействием гидродинамических сил. Практика мо­делирования свидетельствует, что в большинстве случаев это тре­бование можно не учитывать из-за малого его влияния на вели­чину масштабного эффекта.

Условие (6.14) называется критерием Струхала, который яв­ляется определяющим при моделировании нестационарного движе­ния тела в жидкости. Когда движение орудия лова может рас­сматриваться как стационарное, условие (6.14) является условием кинематического подобия течения жидкостей около подобных тел, что обеспечивается автоматически при выполнении остальных ус­ловий подобия.

Таким образом, если условия полного подобия орудий лова описываются системой критерий (6.4) — (6.14), то условия при­ближенного подобия будут различными для разных орудий лова. В каждом конкретном случае они могут быть определены на ос­нове анализа физического существа рассматриваемого процесса.

Значения масштабов подобия рассчитываются, исходя из тре­бования совместного рассмотрения определяющих, для постав­ленной задачи моделирования условий подобия.

Пояснение по решению задач.

Задача 6.17 [1]

Задача решается исходя из определения удельного веса:

γ= 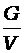, где G – вес , а V – объём предмета.

Связь масштабов подобия выразится формулой: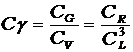

Учитывая, что поплавок находится в воде, нас интересует не сам удельный вес поплавка, а его значение в воде, т.е. получаем выражение (6.2):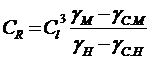

Задача 6.18 [1], критерий Рейнольдса имеет вид:Re = vd/v =idem;

Задача 6.19 [1], Задача решается по критерию Рейнольдса.

,

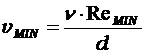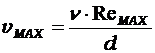
Задача 6.26 [1], Условие подобия Ньютона: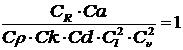

В данных задачи не приводятся значения масштабов подобия Cr и Ck.

Cr принимаем равным 1, т.к. модель как и натура будут буксироваться в воде.

Ck – масштаб коэффициентов сопротивления – рассчитывается на основании зависимости 1.25: , тогда

,

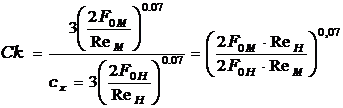F_O определяем по формуле 1.26, считая посадочные коэффициенты модели и натуры одинаковыми. Получаем F_OН= 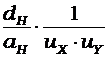, F_OМ= 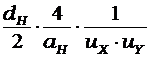, отсюда .

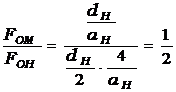Аналогично поступаем с числами Рейнольдса. (см.ф. 1.2)

Вопросы для самоконтроля

1. Охарактеризуйте условия статического, динамического и кинематического подобия.

2. Перечислите основные критерии подобия.

3. Методика расчетов масштабов подобия в условиях недостаточности основных уравнений связи масштабов.
9. Перечень литературы

1. Фридман А.А. «Теория и проектирование орудий промышленного рыболовства». –М.: Легкая и пищевая промышленность. 1981, 328 с.

2. Фридман А.А., Розенштейн М.М. Сборник задач и упражнений по теории и проектированию орудий промышленного рыболовства. –М.: Агропромиздат. 1987, 256с.

3. Кадильников Ю.В. «Вероятно-статистическая теория рыболовных систем и технической доступности для них водных биологических ресурсов». – Калининград: АтлантНИРО. 2001, 275с.

4. Веденеев В.Л. Методические указания по решению задач на тему – тяговые характеристики судов. – Керчь. КМТИ. 2003, –9 с.

5. Веденеев В.Л. Методические указания по выполнению РГР по дисциплине «Механика орудий лова» для студентов специальности 7.100301.11. – Керчь. КМТИ, 2003, 15 с.

© Савотин Дмитрий Вячеславович

Методические указания

к самостоятельной работе студента по дисциплине

«Механика орудий лова»

для студентов направления 6.070104 «Морской и речной транспорт»

специализации «Судовождение и промышленное рыболовство»

Форма обучения - дневная

Тираж __________ экз. Подписано к печати ______________________.

Заказ № _____________. Объем __1,38__п.л.

Изд-во «Керченский государственный морской технологический университет»

98309 г. Керчь, Орджоникидзе, 82.