VII. Элементы теории вероятностей.

Случайные события

Для успешного выполнения упражнений необходимо ознакомиться с элементами комбинаторики, в частности с таким понятием, как сочетания.

Сочетаниями из n элементов по m называются наборы (соединения), составленные из n элементов по m элементов в каждом наборе, которые отличаются хотя бы одним элементом. Например, сочетаниями из девяти первых натуральных чисел по 4 будет: {1;2;3;4},{1;2;5;4},{5;6;7;8},{1;3;5;9} и т.д. Число всех возможных сочетаний из n элементов по m обозначается и вычисляется по формулам:

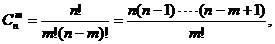где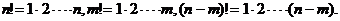

В частности, .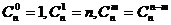

Последняя формула полезна, когда n-m<m. Например,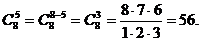

Задача 1. В ящике 9 мышей. Сколько есть способов отобрать четыре из них?

Решение: Искомое число есть число сочетаний из 9 по 4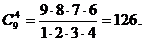

Вопросы для самопроверки:

1. Сформулируйте классическое определение вероятностей случайного события.

2. Что такое сочетания, размещения, перестановки?

3. В каком случае случайные события образуют полную группу?

Сложные события

Вопросы для самопроверки:

1. Что называется суммой двух событий?

2. Какие события называются несовместными?

3. Сформулируйте теорему сложения вероятностей несовместных событий.

4. Что называется произведением двух событий?

5. Каике события называются независимыми?

6. Сформулируйте теорему умножения вероятностей независимых событий.

7. Что называют условной вероятностью?

8. Содержание формулы полной вероятности.

Повторение испытаний

Вопросы для самопроверки:

1. Какая формула и в каких случаях позволяет вычислить вероятность того, что при n испытаниях событие А осуществляется ровно К раз? Как нужно изменить формулу, если необходимо вычислить вероятность того, что при n испытаниях событие А осуществится не менее К₁ и не более К₂ раз.

Тема 12. Случайные величины

Вопросы для самопроверки:

1. Что такое дискретная случайная величина?

2. Что называется функцией распределения? Применимо ли это понятие к дискретным случайным величинам?

3. Какие числовые характеристики случайных величин вы знаете?

4. Исследуйте формулу, задающую нормальное распределение непрерывной случайной величины, и дайте эскиз графика соответствующей функции (кривой Гаусса).

Задачи для самоконтроля:

1. В конверте 10 фотокарточек. Среди них 6 нужных. Наугад извлечены 4 карточки. Найти вероятность того, что среди того, что них 3 нужные.

2. В конверте 12 денежных купюр. Среди них 4 фальшивых. Наугад извлечены 4 купюры. Какова вероятность того, что все они фальшивые?

3. В группе 15 студентов, среди них 5 отличников. Наугад отобраны 4 студента. Найти вероятность того, что среди них 2 отличника.

4. У крольчихи – 8 крольчат, из них 4 белые. Наугад отобрано 2 кролика. Найти вероятность того, что среди них один белый.

5. В корзине 20 грибов среди них 6 белых. Наугад извлечены 4 гриба. Какова вероятность того, что все они белые?

6. В библиотеке 14 учебников по теории вероятностей. Среди них 4 в переплете. Библиотекарь наудачу взял 4 учебника. Какова вероятность того, что все они в переплете.

7. В конверте 9 лотерейных билетов, из них 6 выигрышных. Наугад извлечены 3 билета. Найти вероятность того, что среди них 1 выигрышный.

8. На клумбе растут 20 астр, из них 5 белых. В темноте сорвали 4 астры. Найти вероятность того, что среди них 2 белые.

9. В ящике 12 мышей. Среди них 8 белых. Наугад извлечено 4 мыши. Какова вероятность того, что все они белые.

10. В пенале 10 карандашей, из них 4 цветных. Наудачу извлечены 4 карандаша. Найти вероятность того, что среди них нет цветных.