Тема 4.2. Степенная и показательная функции. Свойства графики.
Самостоятельная работа (4 часа)
Цель: Выработать навык построения графиков степенной и показательной функций.
Показательная функция
y = ax
| y |
| x |
| a>1 |
| a<1 |
| y |
| x |
| y=2x |
| y=0,5x |
| y=3x |
Степенная функция
y = xn
| y |
| x |
| y=x2 |
| y=x4 |
| y |
| x |
| y=x3 |
| y=x5 |
Решить самостоятельно.
Задание. Построить графики функций: y = 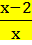 ; y =
; y = 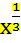 ; y =
; y = 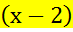 -1
-1
Форма контроля: проверка конспекта и устный опрос.
Самостоятельная работа № 13
Тема 4.3. Логарифмическая функция. Свойства и график.
Самостоятельная работа (2 часа)
· изучить свойства логарифмической функции.
· построение графиков логарифмической функций.
Логарифмическая функция
Функция y= 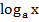 , (х
, (х 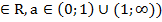 ) называется логарифмической функцией.
) называется логарифмической функцией.
Логарифмическая функция y= 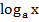 является обратной по отношению к показательной функции у=
является обратной по отношению к показательной функции у= 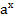 (х
(х 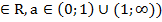 ) . Поэтому их графики симметричны относительно биссектрисы I и III координатных углов (рис. 8).
) . Поэтому их графики симметричны относительно биссектрисы I и III координатных углов (рис. 8).
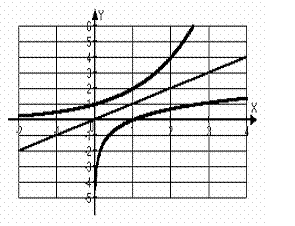
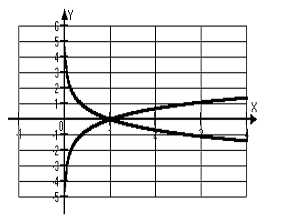
| y |
| x |
| y=log2 x |
| y=log0,4 x |
| y=log4 x |
| y |
| x |
| a>1 |
| a<1 |
Приведем основные свойства логарифмической функции:
1) Область определения: D(y) =R+ .
2) Область значений функции: E(y) =R.
3) Логарифм единицы равен нулю, логарифм основания равен единице: 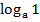 =0,
=0, 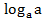 =0, .
=0, .
4) Функция y= 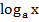 ,
, 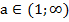 возрастает в промежутке
возрастает в промежутке 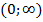 (рис. 8 а). При этом, логарифмы чисел, больших единицы, положительны, а - меньших единицы, отрицательны.
(рис. 8 а). При этом, логарифмы чисел, больших единицы, положительны, а - меньших единицы, отрицательны.
5) Функцияy= 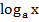 , (х
, (х 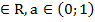 , убывают в промежутке
, убывают в промежутке 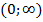 . При этом, логарифмы чисел, меньших единицы, положительны, а - больших единицы, отрицательны.
. При этом, логарифмы чисел, меньших единицы, положительны, а - больших единицы, отрицательны.
4. Найти область определения функции: y= 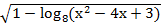
Решение. Поскольку логарифмическая функция определена только для положительных чисел, а квадратный корень – для неотрицательных чисел, задача сводится к решению системы неравенств:
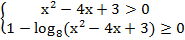
Левую часть первого неравенства разложим на множители, а во втором заменим 1 на 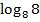 :
:
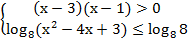
Так как основание логарифма8 >1 , то, согласно свойствам логарифма, переходим к системе: 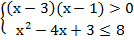 т.е.
т.е. 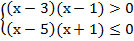
Последняя система равносильна неравенству: 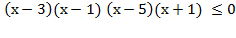 ,
,
которое решается методом интервалов (причем x≠3, и x ≠ 1 ). С помощью рис. 9 получаем ответ:[-1;1) 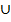 (3;5].
(3;5].
Контрольные вопросы.
1. Дайте определение логарифмической функции.
2. Какие область определения и область значения функции у = logax?
3. В каком случае функция у = logax является возрастающей, в каком убывающей?
4. При каких значениях x функции у = logax принимает положительные значения, при каких отрицательные?
Тест для самопроверки. ( Варианты ответов: да нет)
1. Логарифмическая функция у = logax определена при любом х
2. Функция у = logax определена при а > 0, а =/= 1, х > 0.
3. Областью определения логарифмической функции является множество действительных чисел.
4. Областью значений логарифмической функции является множество действительных чисел.
5. Логарифмическая функция – четная.
6. Логарифмическая функция – нечетная.
7. Функция у = logax – возрастающая при а >1.
8. Функция у = logax при положительном, но меньшем единицы основании, – возрастающая.
9. Логарифмическая функция имеет экстремум в точке (1; 0).
10. График функции у = logax пересекается с осью ОХ.
11. График логарифмической функции находится в верхней полуплоскости.
12. График логарифмической функции симметричен относительно ОХ.
13. График логарифмической функции пересекает ОХ в точке (1; 0).
14. График логарифмической функции находится в 1 и 4 четвертях.
15. Существует логарифм отрицательного числа.
16. Существует логарифм дробного положительного числа.
17. График логарифмической функции проходит через точку (0; 0).
Самостоятельная работа №14
