Шаг 2. Определение начальных координат тел.

В выбранной системе отсчёта начальная координата первого автомобиля равна ____________, а второго — ________________

Шаг 3. Определение проекций скоростей тел на координатную ось.

В выбранной системе отсчёта проекция скорости первого автомобиля на ось X равна __________, а второго автомобиля на ось X равна ______________

Шаг 4. Построение графиков движения тел.

Строим координатную сетку, состоящую из оси времени t (в часах) и оси координаты X (в километрах). Отметим на оси X начальные координаты обоих автомобилей.

Строим графики движения. Так как движение автомобилей равномерное, графики представляют собой _____________________________

Шаг 5. Получение ответа, анализ решения.

Из построения видно, что графики движения автомобилей пересекаются в точке (х_в = ______ км, t_в = _____ ч). Следовательно, в момент времени t_в = ___ (т. е. через _______ после включения секундомера) координаты обоих автомобилей станут равными: ____________________

Таким образом, мы получили ответы на вопросы «Где и когда автомобили встретятся».

Ответ: Машины встретятся на расстоянии l = ________ км от пункта А спустя время t_в = _____ ч после начала движения.

Аналитический способ решения

Задача 2. С Ярославского вокзала вышла электричка, идущая со скоростью, модуль которой υ_э = 60 км/ч. В том же направлении спустя время t₁ = 30 мин вышел скоростной поезд «Спутник», идущий со скоростью, модуль которой υ_с = 90 км/ч. Через какое время t_в после начала движения «Спутника» догонит электричку? На каком расстоянии S от вокзала это произойдёт?

Решение.

Шаг 0. Выбор модели.

Будем считать поезда ________________________________.

Шаг 1. Выбор системы отсчёта.

В качестве тела отсчёта выберем _____________, за начало отсчёта примем ___________________. Координатную ось X направим от ___________________ вдоль путей в направлении ______________________. Часы включим в момент _________________.

Шаг 2. Определение начальных координат тел.

В выбранной системе отсчёта начальная координата «Спутника» _____________________, а электрички — ________________________

Шаг 3. Определение проекций скоростей тел на координатную ось.

В выбранной системе отсчёта направления скоростей обоих поездов совпадает с ____________________ оси X. Поэтому их проекции на ось X ________________ и равны ____________, ____________ соответственно.

Шаг 4. Запись законов движения тел.

Законы движения равномерно движущихся первого и второго поездов с учётом полученных данных имеют вид:

____________________________________________________________

Шаг 5. Запись условия задачи в виде уравнения.

В условии задачи сказано, что в искомый момент времени t_в «Спутник» догнал электричку, т. е. в этот момент времени их координаты стали равными: _______________________________________

Шаг 6. Сведение полученных уравнений в систему и присвоение им названий.

_________________________(2) (закон движения электрички)

_________________________(2) (закон движения «Спутника»)

_________________________(3) (условие встречи)

Шаг 7. Решение системы.

Подставив (1) и (2) для момента времени t = t_вв (3), получим: _________________________________________________________________

Отсюда: t_в = __________, S = _____________

Шаг 8. Анализ полученного результата и расчёт ответа.

Проверкаразмерности полученных результатов.

[t_в] = _____________ и [S] = _______________.

Таким образом, сточки зрения размерности полученный результат _______________________________________.

Исследуем, как будут изменяться полученные значения S и t_в при изменениях величин, входящих в полученные зависимости.

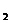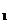Если разность модулей скоростей поездов υ – υ стремится к нулю, то _____________. Если увеличивать скорость «Спутника» υ 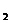при неизменном υ 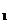, то ___________________. Если уменьшать скорость электрички υ 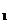при неизменном υ 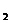, то ____________________.

Полученные выводы _____________ здравому смыслу и жизненному опыту, т. е. полученные ответы __________ физический смысл.

Проводим численный расчёт, подставив в полученное выражение числовые данные: ________________, ________________

Ответ: Поезда встретятся через t_в = _____ ч на расстоянии S = ______ км от станции.

Задача 3. Пешеход и велосипедист движутся навстречу друг другу со скоростями, модули которых равны 2 м/с и 10 м/с соответственно. Расстояние между ними в начальный момент времени равно 240 м. Найдите графическим и аналитическим способами место и время встречи пешехода и велосипедиста.

Решение.

Задача 4. Колонна длиною L, состоящая из физкультурников, которые следуют друг за другом на равных расстояниях, движется с постоянной по модулю скоростью U. Навстречу им бежит тренер со скоростью, модуль которой равен V (V > U). Каждый спортсмен, с которым поравнялся тренер, мгновенно разворачивается и продолжает движение с прежней по модулю скоростью. Определите длину перестроившейся колонны во главе с тренером.

Сложение движений

1. Отметить знаком Ú （галочкой）правильные утверждения:

От выбора системы отсчёта зависят:

только координаты тел; □

только зависимости координат тел от времени; □

только перемещения тел и скорости их движения; □

все перечисленные физические величины. □

2. Дополните предложения, вставляя пропущенные слова.

Если система отсчёта X′Y′ движется поступательно относительно системы отсчёта XY, то

а) перемещение 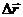точечного тела в системе отсчёта XY равно сумме ____________________ этого тела в системе отсчёта X′Y′ и _____________________ начала системы отсчёта X′Y′ относительно системы отсчёта XY:____________________________;

б) скорость 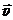точечного тела в системе отсчёта XY равна сумме ___________________ этого тела в системе отсчёта X′Y′ и _________________________, с которой начало отсчёта системы отсчёта X′Y′ движется относительно системы отсчёта XY:

3. Поезд движется относительно платформы со скоростью, модуль которой равен 30 км/ч. По ходу его движения с конца поезда идёт пассажир со скоростью, модуль которой относительно пола вагона равен 1,5 км/ч. Из начала поезда навстречу ему идёт проводник. Модуль его скорости относительно вагона равен 3 км/ч.

а) Определите расстояние, на которое перемещается относительно платформы пассажир:

за 5 мин ______________; за 10 мин _________________;

б) Определите расстояние, на которое перемещается относительно платформы проводник:

за 5 мин ______________; за 10 мин _________________;

в) Определите модули скоростей:

пассажира относительно платформы ________________________км/ч;

проводника относительно платформы _______________________км/ч;

пассажира относительно проводника _______________________км/ч;

проводника относительно пассажира _______________________км/ч.

г) Как изменяется расстояние между пассажиром и проводником:

за 5 мин ___________________; за 10 мин ____________________.

4. Авианосец движется относительно берега моря на запад со скоростью 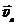, модуль которой равен 10 м/с. С берегом связана система отсчёта XYZ, ось X которой направлена на запад, ось Y — на юг, а ось Z — вверх. Система отсчёта X′Y′Z′, оси которой параллельны соответствующим осям системы отсчёта XYZ, связана с авианосцем. С авианосца взлетает самолёт, перемещаясь относительно его палубы со скоростью, проекция которой на ось 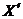равна 100 м/с, а на ось 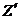равна 5 м/с. Одновременно по палубе бежит офицер со скоростью, проекция которой на ось 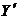равна 2 м/с. Определите величины, указанные в левом столбце, и заполните таблицу.

Величины	Авианосец	Самолёт	Офицер
Перемещение за 1 с:	вдоль оси X′
вдоль оси Y′
вдоль оси Z′
вдоль оси X
вдоль оси Y
вдоль оси Z
Проекция скорости в системе отсчёта 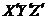:	на ось X′
на ось Y′
на ось Z′
Проекция скорости в системе отсчёта 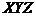:	на ось X
на ось Y
на ось Z

5. Модуль скорости течения реки шириной L = 4 м равен 2 м/с. Направление скорости течения реки совпадает с положительным направлением оси X, связанной с берегом. Ось Y направлена горизонтально и перпендикулярно оси X. Собака переплывает реку так, что проекция её скорости относительно воды на ось Y равна 1 м/с, а на ось X отрицательна и равна –0,5 м/с. Сделайте рисунок и изобразите:

1) перемещение за первую секунду: собаки относительно воды 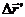— синим карандашом; воды относительно берега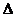 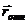— зелёным карандашом;

собаки относительно берега 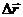— красным карандашом.

2) указанные перемещения за последующие секунды переправы.

Определите по рисунку: а) время переправы; б) смещение Dx собаки вдоль берега за время переправы.

Ответ: время переправы Dt = ______ с; снос ∆х = ________ м.

6. Известно, что при движении велосипедиста и бегуна в одном направлении бегун отстаёт от велосипедиста на S 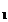= 120 м за каждую минуту, а если они движутся навстречу друг другу, не меняя модулей скорости, то расстояние между ними уменьшается на S 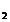= 600 м за каждые две минуты. Определите модули скорости велосипедиста и пешехода.

Решение.

Ответ: модуль скорости велосипедиста v₁ = ________ м/с;

модуль скорости бегуна v₂ = __________ м/с.

7. Сколько времени займёт рейс лодки по прямой от пристани А до пристани В (на другом берегу вниз по течению) и обратно, если модуль скорости течения постоянен и всюду равен ? Модуль скорости лодки относительно воды равен v; расстояние вдоль берега от пристани А до точки, расположенной напротив пристани В, равно 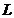; ширина реки — .

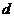8. На противоположных берегах прямолинейного участка реки находятся две пристани А и В, расстояние между которыми S = 130 м, а прямая АВ составляет угол a = 60° с берегом. Модуль скорости воды по всей ширине реки одинаков и равен u = 0,1 м/с. С пристаней одновременно отплыли два катера и, двигаясь все время по прямой АВ с постоянными относительно воды скоростями, модули которых равны, встретились через t = 36 с. Определите модуль v скорости катеров относительно воды.

9. В вершинах равностороннего треугольника с длиной стороны L находятся три черепахи, размеры которых много меньше L. Первая черепаха смотрит на вторую, вторая — на третью, а третья — на первую. В некоторый момент черепахи начинают двигаться с одинаковыми по модулю скоростями. При этом каждая черепаха в любой момент времени движется в направлении той черепахи, на которую она смотрит. Определите время движения черепах до их встречи в центре квадрата.