Автоматизированные системы обработки информации и управления» (по отраслям)
Автоматизированные системы обработки информации и управления» (по отраслям)
Программное обеспечение вычислительной техники и автоматизированных систем»
Техническое обслуживание средств вычислительной техники и компьютерных сетей»
Часть 1
Идентификационный номер – дсмк – 2.4 АС ЕН.01
|
Ярославль 2010 г.
Рассмотрено и одобрено
на заседании кафедры ОБЩ
Протокол № 3 от 07.10.2009 г.
Руководитель кафедры:
____________ Шереметьева Н.В.
Составители:
· преподаватели Шереметьева Н.В.и Холманова В.М.
Рецензенты:
· зам. директора по НМР и КО ЯТЖТ Лебедев М.К.;
· преподаватель математики высшей квалификационной категории ЯГК Колесникова Л.Л.
Аннотация
Данная работа представляет собой учебно-методическое пособие по организации самостоятельной внеаудиторной работы студентов по дисциплине «Математика (Элементы высшей математики» для специальностей 230103 «Автоматизированные системы обработки информации и управления» (по отраслям), 230105 «Программное обеспечение вычислительной техники и автоматизированных систем», 230106 «Техническое обслуживание средств вычислительной техники и компьютерных сетей».
Работа включает в себя рекомендации по работе с данным учебным пособием, задания для самостоятельной внеаудиторной работы, методические рекомендации по их выполнению с образцами решения типовых задач, основными правилами и формулами, а также критериями оценки выполнения самостоятельной работы. В работе представлены не только типовые задания, но и задачи повышенного уровня для студентов, увлеченных математикой, задания с нестандартной формулировкой, позволяющие вскрыть интересные факты из жизни гениальных математиков.
Материалы, изложенные в пособии, помогут студентам систематизировать и закрепить полученные на аудиторных занятиях по математике теоретические знания, сформировать практические навыки, активизировать учебно-познавательную деятельность.
СОДЕРЖАНИЕ
| Пояснительная записка. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Рекомендации по работе с учебно-методическим пособием. . . . . . . . . . . . . . . . | |
| Рекомендации по выполнению разных видов самостоятельной работы. . . . . | |
| Задания для самостоятельной работы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Введение | |
| Задание 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Раздел 1. Элементы линейной алгебры | |
| Задание 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Задание 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Задание 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Задание 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Раздел 2. Элементы аналитической геометрии | |
| Задание 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Задание 7 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Задание 8 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Раздел 3. Основы математического анализа Тема 3.1. Теория пределов. Непрерывность | |
| Задание 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Задание 10 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Задание 11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Тема 3.2. Дифференциальное исчисление функции одной действительной переменной | |
| Задание 12 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Задание 13 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Задание 14 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Задание 15 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Задание 16 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Задание 17 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Задание 18 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |
| Критерии оценки выполнения самостоятельной работы. . . . . . . . . . . . . . . . . . . | |
| Список рекомендуемой литературы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Согласно требованиям государственного образовательного стандарта среднего профессионального образования каждый студент обязан выполнить по каждой учебной дисциплине определенный объем внеаудиторной самостоятельной работы.
Методические указания по выполнению внеаудиторной самостоятельной работы составлены для студентов специальностей 230103 «Автоматизированные системы обработки информации и управления» (по отраслям), 230105 «Программное обеспечение вычислительной техники и автоматизированных систем», 230106 «Техническое обслуживание средств вычислительной техники и компьютерных сетей». Цель методических указаний состоит в обеспечении эффективности самостоятельной работы, определении ее содержания, установления требований к оформлению и результатам самостоятельной работы.
Целями самостоятельной работы студентов по дисциплине «Математика (Элементы высшей математики)» являются:
· систематизации и закрепления полученных теоретических знаний и практических навыков;
· развитие навыков применения полученных знаний при решении конкретных прикладных задач;
· углубление и расширение теоретических знаний;
· формирование умений использовать справочную и дополнительную литературу;
· развитие познавательных способностей и активности студентов, творческой инициативы, самостоятельности и самоорганизации;
· активизации учебно-познавательной деятельности будущих специалистов.
Рабочей программой дисциплины «Математика (Элементы высшей математики)» предусмотрены следующие виды внеаудиторной самостоятельной работы:
1. изучение материала лекций или учебника, составление опорных конспектов;
2. решение задач;
3. подготовка докладов, сообщений;
4. подготовка презентаций;
5. выполнение домашних контрольных работ.
Содержание самостоятельной работы по каждой теме, количество часов, предусмотренных на ее выполнение, формы контроля выполнения работы представлены в следующей таблице:
| № темы | Содержание самостоятельной работы | Объем в часах | Формы контроля | ||
| АС | ПО | ТО | |||
| Введе- ние | 1. Подготовка докладов (презентаций) о роли математики в современном мире | 1,5 | 1,5 | 1,5 | устная проверка |
| 1.1 | 2. Решение задач на действия над матрицами 3. Нахождение определителей п-го порядка, миноров и алгебраических дополнений 4. Нахождение обратной матрицы, вычисление ранга матрицы | 0,5 | 0,5 | 0,5 | выбор. письм. контроль выбор. письм. контроль выбор. письм. контроль |
| 1.2 | 5. Решение систем линейных уравнений по правилу Крамера и методом Гаусса | выбор. письм. контроль | |||
| 2.1 | 6. Операции над векторами в координатах | выбор. письм. контроль | |||
| 2.2 | 7. Составление уравнений прямых. 8. Составление уравнений кривых второго порядка и их построение | 0,5 | 0,5 | 0,5 | выбор. письм. контроль выбор. письм. контроль |
| 3.1 | 9. Виды числовых последовательностей. Определение пределов последовательностей 10. Вычисление пределов функции с помощью замечательных, раскрытие неопределенностей 11. Решение задач нахождение и классификацию точек разрыва функции | 0,5 | - | выбор. письм. контроль выборочный письм. контроль выбор. письм. контроль | |
| 3.2 | 12. Решение задач на нахождение производных и дифференциалов с использованием правил и формул дифференцирования 13. Нахождение производной сложной функции 14. Решение задач на нахождение производных высших порядков, раскрытие неопределенностей по правилу Лопиталя 15. Решение задач на определение промежутков возрастания и убывания, нахождение экстремумов функции 16. Определение промежутков выпуклости, вогнутости функций, нахождение точек перегиба 17. Нахождение асимптот графика функции 18. Выполнение домашней контрольной работы по исследованию функции и построению ее графика | 0,5 0,5 0,5 1,5 | 0,5 1,5 | 0,5 0,5 0,5 0,5 1,5 | выборочный письменный контроль выбор. письм. контроль выборочный письм. контроль выборочный письм. контроль выбор. письм. контроль выбор. письм. контроль письменный контроль |
| Итого | 17,5 |
Каждое задание включает в себя:
- название раздела (в соответствии с рабочей программой);
- название темы;
- цель выполнения работы;
- формулировку заданий для самостоятельной внеаудиторной работы:
&- задания, предполагающие актуализацию теоретических знаний;
? - задания для письменного решения;
¶ - дополнительные задания повышенного уровня сложности;
i - интересные задания, направленные на развитие познавательной активности студентов посредством открытия фактов из истории жизни и деятельности творцов науки;
- методические указания по выполнению работы;
- список литературы.
Хочется верить, что данное пособие поможет студентам в правильной организации их самостоятельной работы, даст возможность получить прочные и глубокие знания, добиться хорошо сформированных умений по дисциплине «Математика (Элементы высшей математики)», а главное - может послужить ступенькой к их дальнейшему самосовершенствованию и творческой самореализации.
РЕКОМЕНДАЦИИ ПО РАБОТЕ С УЧЕБНО-МЕТОДИЧЕСКИМ ПОСОБИЕМ

Уважаемые студенты!
Прежде чем приступить к выполнению заданий, прочтите рекомендации по работе с данным учебно-методическим пособием.

Главное, чему Вы должны научиться при изучении математики – умению мыслить, анализировать, рассуждать, и, конечно же, решать задачи.
Задания для письменного решения обозначены в пособии символом ?,
САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Как самостоятельно изучить теоретический материал
Прежде чем приступать к решению задач, необходимо внимательно изучить теоретический материал учебника или конспект лекции.
Советуем Вам соблюдать следующие правила:
Правило 1. Внимательно прочтите материал несколько раз. Это не займет много времени, но совершенно необходимо, так как, какими бы большими математическими способностями ни обладал человек, после одного - двух прочтений нового материала обычно невозможно полноценно усвоить его содержание.
При первом прочтении нужно ставить цель - понять, а не запомнить. Обычно для достижения хорошего понимания материала одного прочтения мало. К тому же часто приходится, полистав книгу или конспект лекций, припомнить кое-что из ранее изученного.
А для того, чтобы хорошо запомнить главное (основные утверждения, формулы и т.п.) необходимо второе, а иногда и третье прочтение.
Правило 2. Повторите по памяти формулировку основных правил, понятий, теорем из изученного параграфа. Только тогда вы приобретете знания, ради которых изучается курс.
Правило 3. Разберите типовые примеры и решение ключевых задач по данной теме. Тогда Вы поймете, как усвоенные теоретические знания могут применяться в различных ситуациях.
Правило 4. Ответьте на контрольные вопросы, не заглядывая в книгу или в тетрадь. Обычно контрольные вопросы приведены в конце каждого параграфа учебника. Попробуйте оценить свои знания, сравнив свой ответ с текстом книги или конспекта лекции.
Правило 5. Самостоятельно решите предложенные задачи по данной теме.
Только при выполнении всех этих правил Вы можете быть уверены, что теоретический материал по данной теме Вами усвоен.
Как подготовить доклад
Помните, что доклад – публичное сообщение на определенную тему.
Доклад имеет следующую структуру:
· план;
· основную часть;
· выводы и обобщения;
· список использованной литературы.
При подготовке доклада удобно соблюдать следующий порядок работы:
1. Подберите литературу по изучаемой теме, познакомьтесь с ее содержанием.
2. Отметьте или выпишите ключевые моменты, раскрывающие данную тему. Продумайте, как можно изложить основной текст кратко, но с минимальными информационными потерями: что исключить? что обобщить?
3. Составьте план доклада.
4. Используя составленный план, напишите текст доклада:
- в начале доклада необходимо обосновать выбор темы, показать ее актуальность; чтобы доклад был интересен слушателям, сформулируйте проблемный или оригинальный вопрос по теме выступления;
- в основной части доклада раскройте каждый пункт плана; старайтесь использовать только понятную Вам информацию, иллюстрируя ее яркими, образными, запоминающимися примерами;
- в заключении доклада кратко изложите основные мысли, затронутые в докладе; выразите свое отношение к излагаемой теме и ее содержанию; для резюмирования можно использовать фразы: «таким образом…», «итак…», «можно утверждать…», «основная идея, следовательно, сводится к следующему…», «подытожим сказанное…».
5. Прочитайте текст доклада и отредактируйте его.
6. Оформите текст доклада в соответствии со структурой. Если Вы будете набирать текст доклада на компьютере, то используйте шрифт Times New Roman № 12, междустрочный интервал одинарный, поля по 2 см, снизу по центру – нумерация страниц. По-возможности текст доклада могут иллюстрировать картинки, рисунки и фотографии.
7. Оформите титульный лист следующим образом:

Федеральное государственное образовательное учреждение
среднего профессионального образования
«Ярославский градостроительный колледж»
Доклад на тему «_______________________»
Дисциплина: Математика
Выполнил: студент группы ___
__________________________
Проверил: преподаватель
____________________________
Ярославль, ____ год
Как создать презентацию
Помните, что презентация – это последовательность слайдов с текстовой информацией и визуальными материалами (рисунками, фотографиями, диаграммами, видеороликами).
Презентация по заданной тематике должна иметь следующую структуру:
1. титульный слайд (название работы, авторы);
2. план презентации (желательно наличие гиперссылок для удобства перехода к нужным слайдам);
3. основная часть;
4. заключение (краткое изложение основных мыслей, отношение автора к излагаемой теме и ее содержанию);
5. список использованной литературы.
При подготовке презентации удобно соблюдать тот же порядок работы, что и при подготовке доклада.
При оформлении презентации продумайте, как будет представлена информация на каждом слайде. Используйте следующие рекомендации:
1. По содержанию информации:
ü используйте короткие слова и предложения, выражающие основную мысль;
ü минимизируйте количество предлогов, наречий, прилагательных;
ü дополните текстовую информацию визуальными материалами (фотографиями, формулами, рисунками…);
ü структурируйте информацию, выделяйте ключевые слова, термины, понятия.
2. По объёму информации:
ü не заполняйте один слайд слишком большим объемом информации;
ü используйте не более 7 строк на слайде.
3. По расположению информации на слайде:
ü отдавайте предпочтение горизонтальному расположению информации;
ü продумайте подписи изображений.
4. По оформлению слайдов:
ü соблюдайте единый стиль оформления презентации.
ü при выборе шрифта
· используйте шрифты без засечек (Arial, Franklin и др.);
· для заголовков – размером не менее 24 пунктов;
· для информации – размером не менее 18 пунктов;
· для выделения применяйте жирный шрифт или курсив.
ü при выборе цвета:
· для фона выбирайте светлые тона;
· для фона и текста используйте контрастные цвета;
· на одном слайде применяйте не более трёх цветов.
ü при выборе эффектов анимации:
· анимационные эффекты не должны отвлекать от содержания информации на слайде;
· не применяйте анимации к заголовкам на пустом слайде.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Введение
Задание 1. Подготовка докладов (презентаций) о роли математики
В современном мире – 1,5 ч.
Цель: расширение кругозора студентов в области приложения знаний по дисциплине, развитие творческих способностей студентов.
Задание для самостоятельной внеаудиторной работы:
?1.1. Подберите литературу и оформите письменный доклад или создайте электронную презентацию по одной из тем:
- «Роль математики в современном мире»;
- «Математика и моя будущая профессия»;
- примеры прикладных задач, при решении которых применяется аппарат высшей математики.
Список литературы:
1. Валуце И.И. Математика для техникумов на базе средней школы: Учеб. пособие / И.И. Валуце, Г.Д. Дилигул. – М.: Наука, 1989. – Введение, стр. 5.
2. Материалы сети Интернет.
3. Источники литературы, найденные самостоятельно.
Задание 2. Решение задач на действия над матрицами – 0,5 ч.
Цель:формирование умения находить линейную комбинацию, произведение матриц, транспонировать матрицу.
Задание для самостоятельной внеаудиторной работы:
& 2.1.Выучите, что называют матрицей, какие основные операции над матрицами существуют.
?2.2.Заданы матрицы: 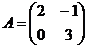 ,
, 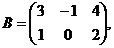
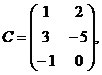
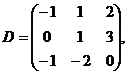
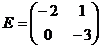 . Какие из следующих операций выполнимы:
. Какие из следующих операций выполнимы:
а) А+В; б) А-Е; в) В+С; г) ВТ+2С; д) А∙В; е) А∙С; ж) В∙С; з) В∙D; и) СТ∙D?
?2.3.Заданы матрицы: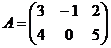 ,
, 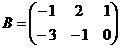 . Найдите:
. Найдите:
а) 2А; б) 3В; в) 2А+3В; г) 2А-3В; д)ВТ; е) А∙ВТ;ж)ВТ∙А.
¶2.4. Найдите матрицу: а) 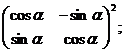 б)
б)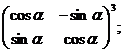 в)
в)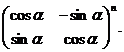
Методические указания по выполнению работы:
При решении задач необходимо знание следующего теоретического материала:
Матрицей размера (m x n) (m и n - натуральные числа) называется совокупность чисел, расположенных в виде прямоугольной таблицы, состоящей из m строк и n столбцов.
При решении задач 2.2 – 2.4 проанализируйте, какие операции нужно выполнить над матрицами. Внимательно изучите следующий теоретический материал и разберите примеры решения типовых задач:
Операции над матрицами.
1. Транспонирование матриц
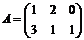 Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной и обозначается Ат.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной и обозначается Ат.
Пример 1.Транспонируйте матрицу
Решение. Операция транспонирования матрицы А осуществляется следующим образом: первая строка матрицы А становится первым столбцом матрицы АТ , вторая строка А - вторым столбцом Ат, т.е.
Ат = 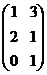
2. Сложение (вычитание) матриц
Складывать (вычитать) можно только такие матрицы, которые имеют одинаковую размерность.
Суммой (разностью) матриц А = (aij) и В = (bij) называется матрица С, элементы которой равны суммам (разностям) соответствующих элементов матриц А и В, т.е. cij = aij + bij (cij = aij - bij).
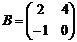 | |||
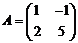 | |||
Пример 2. Найдите сумму и разность матриц и
Решение:
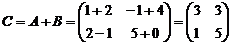 |
D = A – B = 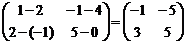
3. Произведениемматрицы А = (аij) на число k (k 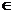 R) называется матрица С той же размерности, элементы которой равны произведению числа k на соответствующие элементы матрицы А, т.е. cij = k · аij
R) называется матрица С той же размерности, элементы которой равны произведению числа k на соответствующие элементы матрицы А, т.е. cij = k · аij
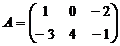 Пример 3. Найдите произведение матрицы А на число k = 3, если
Пример 3. Найдите произведение матрицы А на число k = 3, если
Решение:
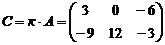 |
4. Умножение матриц
Матрицу А можно умножать на матрицу В тогда и только тогда, когда число столбцов матрицы А равно числу строк матрицы В.
 Произведением матрицы А размера (m x n) на матрицу В размера (п x р) называется матрица С = (сij) размера (m x р), элементы которой равны сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-гo столбца матрицы В.
Произведением матрицы А размера (m x n) на матрицу В размера (п x р) называется матрица С = (сij) размера (m x р), элементы которой равны сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-гo столбца матрицы В.
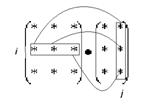
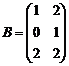 Получение элемента сij можно представить в виде схемы (рис. 1):
Получение элемента сij можно представить в виде схемы (рис. 1):
| |||
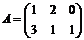 | |||
Пример 4.Найдите произведение матриц и .
Решение. Размер матрицы А (2 х 3), размер В - (3 х 2).
Число столбцов матрицы А равно числу строк матрицы В, следовательно, умножение возможно. При этом матрица С = А ·В будет иметь размерность (2 х 2).
Найдем элементы сij матрицы С:
Для нахождения элемента c11 находим сумму произведений элементов первой строки матрицы А и первого столбца матрицы В:
c11 = (1 строка А и 1 столбец В) = l ·1 + 2· 0 + 0 · 2 = 1;
Аналогично c12 = (1 строка А и 2 столбец В) = 1 · 2 + 2 · 1 + 0 · 2 = 4;
c21= (2 строка А и 1 столбец В) = 3 · 1 + 1 · 0 + 1 · 2 = 5;
c22= (2 строка А и 2 столбец В) = 3 · 2 + 1 · 1 + 1 · 2 = 9.
 | |||
 | |||
Получили, что . Ответ:
Список литературы:
1. Григорьев В.П. Элементы высшей математики: Учеб. для студ. учреждений СПО / В.П.Григорьев, Ю.А.Дубинский - М.: Издательский центр "Академия", 2004. – 320с. – Глава 2, §2.1, стр. 12 – 17.
2. Лисичкин В.Т. Математика: учеб. пособие для техникумов / В.Т. Лисичкин, И.Л. Соловейчик. – М.: Высш. школа, 1991. – 480 с. – Глава 1, §1, стр. 63 – 71.
Задание 4. Нахождение обратной матрицы, вычисление ранга матрицы – 1 ч.
Цель: формирование умения находить обратную матрицу, вычислять ранг матрицы.
Задание для самостоятельной внеаудиторной работы:
&4.1.Выучите, какую матрицу называют обратной данной. Разберите алгоритм нахождения обратной матрицы. Продумайте, как осуществить проверку правильности решения.
?4.2. Найдите обратную для заданной матрицы (если она существует):
а) 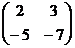 ; б)
; б) 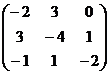 ; в)
; в) 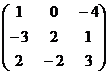 .
.
Выполните проверку правильности нахождения обратной матрицы.
&4.3.Разберите, что называют рангом матрицы, какие преобразования необходимо выполнять для приведения матрицы к ступенчатому виду.
?4.4. Найдите ранг матрицы:
а) 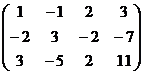 ; б)
; б) 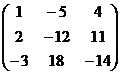 .
.
¶4.5. Найдите ранг матрицы: 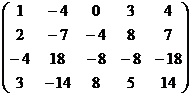 .
.
Методические указания по выполнению работы:
При решении задач необходимо знание следующего теоретического материала:
Матрица А-1 называется обратной для матрицы А, если выполняется условие: А-1·А = А ·А-1= =Е, где Е – единичная матрица того же порядка, что и матрица А.
Матрица называется единичной, если её элементы, стоящие на главной диагонали, равны 1, остальные элементы равны нулю.
Теорема. Квадратная матрица имеет обратную, если 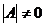 .
.
Для нахождения обратной матрицы удобно использовать следующий алгоритм:
Задание 5. Решение систем линейных уравнений по правилу Крамера и методом Гаусса – 1 ч.
Цель: формирование умения решать системы линейных уравнений по правилу Крамера и методом Гаусса.
Задание для самостоятельной внеаудиторной работы:
& 5.1.Изучите теоретические основы решения системы линейных уравнений по правилу Крамера и методом Гаусса.
?5.2. Решите систему уравнений, используя правило Крамера:
а) 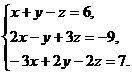 б)
б) 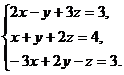
?5.3. Решите систему линейных уравнений по методу Гаусса:
а) 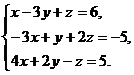 б)
б) 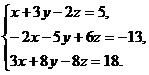 в)
в) 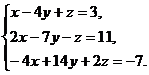
¶5.4. Фирма для перевозки грузов может заказывать машины трех видов. Если она закажет по одной машине каждого вида, то перевезёт 12 тонн груза. Если закажет по две машины первого и второго вида и одну машину третьего вида, то перевезёт 19 тонн груза. Если же фирма закажет по две машины первого и третьего вида и одну машину второго вида, то перевезёт 20 тонн груза. Какова грузоподъемность каждого вида машин?
Методические указания по выполнению работы:
Для решения систем линейных уравнений применяют правило Крамера и метод Гаусса.
Задание 6. Операции над векторами в координатах – 1 ч.
Цель: формирование умения выполнять основные операции над векторами в координатах.
Задание для самостоятельной внеаудиторной работы:
&6.1.Выучите определение свободного вектора, координат вектора на плоскости. Пользуясь обобщающей таблицей, проанализируйте, какие операции над векторами в координатах выполнимы, в чем заключаются признаки коллинеарности и перпендикулярности векторов.
i6.2. В треугольнике 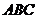 вершины имеют координаты
вершины имеют координаты 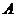 (2; -1),
(2; -1), 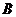 (5; -5),
(5; -5), 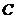 (8; -5). Найдите:
(8; -5). Найдите:
1) координаты вектора 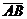 ;
;
2) длину стороны 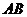 ;
;
3) координату точки 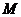 - середины отрезка
- середины отрезка 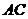 ;
;
4) длину медианы 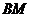 ;
;
5) координаты вектора 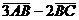 ;
;
6) косинус угла между векторами 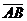 и
и 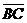 ;
;
 ¶7) треугольник
¶7) треугольник 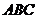 достроили до параллелограмма
достроили до параллелограмма 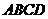 ; найдите координату вершины
; найдите координату вершины 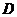 .
.
Решив задания 1 - 6 и заменив получившиеся ответы буквами из таблицы, Вы узнаете, какой профессии были отданы три года жизни создателя аналитической геометрии Рене Декарта (1596-1650).
Профессия:
Карта ответов:
| Е | И | Й | Н | О | Р | У | Ф | Ц | Ч | Ы |
| (3;-12) | (5;-3) | (-3;4) | (3;-4) | 0,6 | 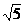 | (10;-6) | -0,2 |
?6.3. При каком значении т векторы 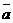 = (-4; 1) и
= (-4; 1) и 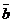 =(т; -2)
=(т; -2)
а) взаимно перпендикулярны; б) коллинеарны.
¶6.4. Докажите, что 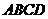 , где
, где 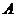 (-2; 1),
(-2; 1), 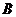 (1; 2),
(1; 2), 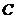 (4; -1),
(4; -1), 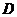 (-2; -3) – трапеция с основаниями
(-2; -3) – трапеция с основаниями 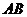 и
и 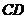 . Определите, является ли трапеция равнобокой. На оси ОХ найдите координаты точки, равноудаленной от точек А и В.
. Определите, является ли трапеция равнобокой. На оси ОХ найдите координаты точки, равноудаленной от точек А и В.
Методические указания по выполнению работы:
Вектор – это направленный отрезок. Все равные между собой направленные отрезки называют свободнымвектором.
Коэффициенты (x; y) разложения вектора 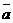 по векторам
по векторам 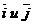 (единичным взаимно перпендикулярным векторам)
(единичным взаимно перпендикулярным векторам) 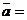
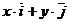 называют координатами вектора на плоскости.
называют координатами вектора на плоскости.
При решении задач по теме «Векторы» используйте следующие рекомендации:
- Выпишите исходные данные – дано. Если в условии задачи сказано о коллинеарности, перпендикулярности, равенстве длин векторов, то это также необходимо выписать.
- Определите, что нужно найти или что доказать в соответствии с условием задачи.
- Опираясь на то, что нужно найти, попытайтесь поискать ключ к решению: выбрать в таблице нужные операции или использовать признаки коллинеарности и перпендикулярности векторов, сформулированные в теоремах 1 и 2.
Задание 7. Составление уравнений прямых – 0,5 ч.
Цель: формирование умения составлять уравнения прямых на плоскости.
Задание для самостоятельной внеаудиторной работы:
&7.1.Опираясь на обобщающие таблицы, изучите, какими способами можно задать прямую, и какие виды уравнения прямой существуют.
?7.2. В треугольнике 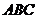 заданы координаты вершин
заданы координаты вершин 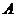 (-5; 3),
(-5; 3), 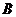 (2; -1),
(2; -1), 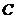 (6; 3). Составьте уравнение:
(6; 3). Составьте уравнение:
а) прямой 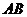 ;
;
б) медианы 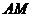 ;
;
в) прямой, проходящей через точку 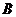 параллельно
параллельно 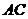 ;
;
г) прямой, проходящей через точку 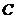 с угловым коэффициентом
с угловым коэффициентом 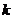 =3.
=3.
¶7.3. 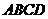 - трапеция с основаниями
- трапеция с основаниями 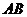 и
и 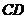 , в которой
, в которой 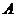 (-2; 1),
(-2; 1), 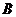 (1; 2),
(1; 2), 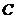 (4; -1),
(4; -1), 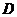 (-2; -3).
(-2; -3).
Составьте уравнение:
а) диагонали 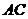 в каноническом виде;
в каноническом виде;
б) прямой, параллельной основаниям, проходящей через точку 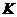 (-3; -1) в параметрическом виде;
(-3; -1) в параметрическом виде;
в) прямой, проходящей через точку 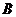 и образующей с положительным направлением оси
и образующей с положительным направлением оси 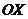 угол
угол 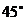 (вид уравнения прямой – с угловым коэффициентом);
(вид уравнения прямой – с угловым коэффициентом);
г) средней линии трапеции в каноническом виде;
д) прямой, проходящей через точку 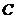 параллельно прямой
параллельно прямой 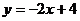 .
.
¶7.4. Запишите уравнение прямой во всех видах (общем, каноническом, параметрическом, с угловым коэффициентом) и постройте эту прямую:
а) 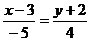 ; б)
; б) 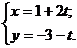
Методические указания по выполнению работы:
Уравнением линиина плоскости называется уравнение с двумя переменными x и y, которому удовлетворяют координаты любой точки, лежащей на линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Прямые – самые простые линии на плоскости. Им соответствуют уравнения первой степени.
При решении задач удобно использовать следующие обобщающие таблицы:
Способы задания прямой
| № | Способ задания | 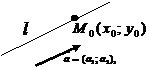 Исходные данные Исходные данные | Уравнение прямой |
| С помощью точки и направляющего вектора | 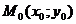 , , 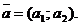 | 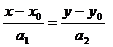 | |
| Через две точки | 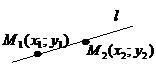 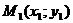 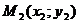 | 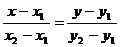 | |
| Через точку с заданным угловым коэффициентом | 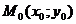 k = tg k = tg |
