Двумерные «подмодели» многомерных моделей.

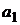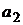Естественно, что в реальной практике редко ограничиваются портфелем из двух активов, однако полученные выше результаты могут быть использованы и в общем многомерном случае, если в качестве двух активов и рассматривать два портфеля 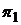и 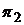с представляющими их векторам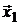и и . .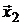

Другими словами, мы портфель 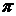, состоящий из 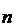активов 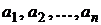, можем представить в виде линейной комбинации:

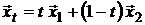(13)

портфеле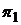й и 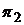, состоящих из 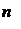активов 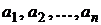каждый.

И если параметры рынка ценных бумаг имеют вид:

,

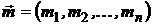то средние доходности портфелей равны:

;

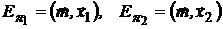а риски вычисляются как:

;

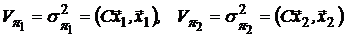ковариация между доходностями портфеле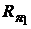й и 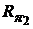будет равна:

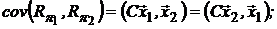
а коэффициент корреляции:

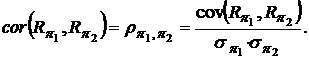
Тогда можно вычислить оценки портфелей 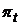, определяемых соотношением (13):

,

.

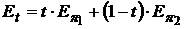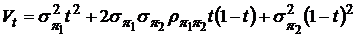Эти соотношения аналогичны соотношениям (6) и (7), поэтому геометрия портфеля 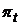будет аналогична рассмотренным выше двумерным множествам. Это означает, что портфель (13) описывает прямую 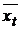в пространстве всех портфелей 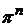, на критериальной плоскости 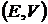будем иметь параболу, а на 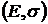- гиперболу или пару лучей:

Рис.19.

Если речь идет о модели Марковица, то необходимо выполнение условий:

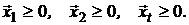
Это означает, что допустимыми являются: отрезок 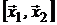прямой 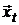, дуга параболы или гиперболы 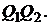Эти «отрезки» выделены на рис. 19 более жирным шрифтом.

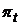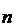Приведенная выше схема построения портфеля из активов 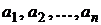и получения их оценок 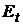и 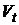может применяться к любой паре портфелей 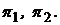В частности, из вышесказанного следует, что критериальное множество в 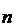- мерной модели обязательно выпукло вниз.

Действительно, пусть критериальное множество имеет вид:

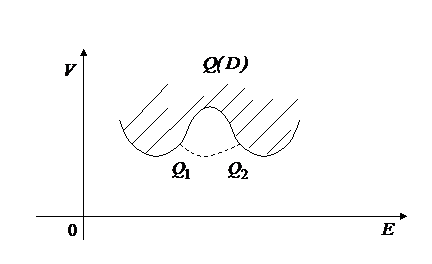
Рис.20.

Тогда для любых двух портфеле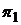й и 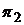, с оценкам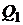и и 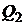, лежащими на минимальной границе, получили бы для портфеля 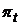(13) оценки, лежащие на дуге параболы 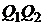. Все оценки такого типа должны принадлежать критериальному множеству, поэтому граница критериального множества не может иметь вид, указанный выше.

МОДЕЛИ С ТРЕМЯ АКТИВАМИ

Для двумерных моделей, рассмотренных выше, критериальные множества представляли собой линии на плоскости, и граница критериального множества совпадала с самим множеством. Для моделей с числом активов более двух критериальное множество будет содержать и внутренние точки. Рассмотрим для примера модель Марковица с тремя активами, а именно

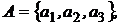
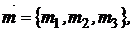
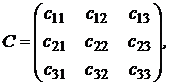
Каждый портфель 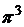описывается вектором:

,

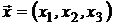с ограничением , .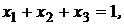

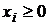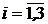Пусть 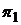, , 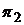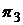- портфели, составленные только из одного актива с векторами:

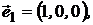
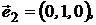
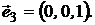
а 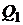, , 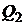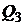- соответственно – оценки этих портфелей на критериальной плоскости.

Класс всех трехмерных портфелей модели Марковица представляет собой двумерный комплекс 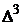в трехмерном пространстве:

Рис.21.

с вершинами в единичных точках. А образы отрезков 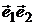, , 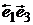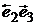на критериальной плоскости 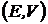будут дугами парабол 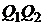, , 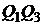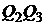соответственно; а критериальное множество будет представлять собой криволинейный треугольник.

Рис.22.

Если же эти дуги пересекаются, как на следующем рисунке, то, вроде бы, получается критериальное множество, состоящее из трех криволинейных треугольников.

Рис.23.

Однако мы уже знаем, что минимальная граница критериального множества должна быть выпуклой линией. Поэтому, взяв, например, оценки портфеле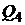й и 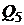для достижения линейной комбинации этих портфелей, получим дугу параболы 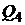и 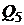. Повторив многократно этот процесс с различными оценками трехмерных портфелей, придем к критериальному множеству в виде одного криволинейного треугольника, только при этом границы будут состоять не из одной параболы, а из кусков парабол.

Возможны и другие виды критериального множества, например,

Рис.24.

Или, если в портфель входит безрисковый актив (пусть это портфель с оценкой 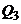), то критериальное множество будет иметь вид:

Рис.25.

то есть она будет касаться оси абсцисс.

На критериальной плоскости 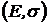критериальное множество строится из кусков гипербол или прямолинейных отрезков. Например, если в портфель входит безрисковый актив с оценкой 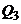, то типичное критериальное множество будет иметь вид

Рис.26.

Отметим, что до сих пор мы строили критериальное множество на критериальной плоскости, в которой (для удобства) доходность отмечали на оси абсцисс, а риск на оси ординат. Однако в финансовой литературе действует и обратное правило, согласно которому типичные критериальные множества для моделей Блека и Марковица изображаются следующим образом:

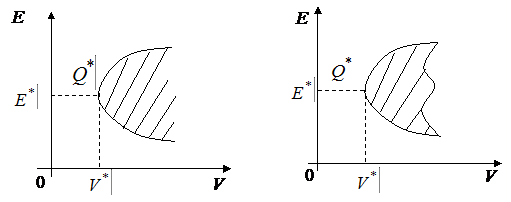Рис.27.