Модель марковица для двух активов

В этой модели, к основному ограничению

,

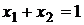добавляются условия не отрицательности: 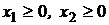. Или

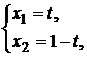
при условии, что .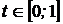

Следовательно, доходность и риск будут оцениваться по тем же формулам (6) и (7), только при этом следует учитывать, что параметр 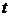удовлетворяет ограничению 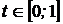. Это означает, что критериальное множество в модели Марковица будет представлять собой подмножество критериального множества модели Блека. Геометрически это означает дугу параболы (гиперболы) между оценкам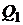и и 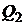активов 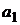и .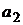

Тогда для различных значений коэффициента корреляции 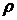можем получить следующие критериальные множества.

При 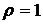на плоскости 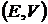получаем дугу параболы 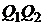, а на плоскости 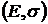-отрезок прямой :

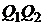Рис.13.

Здесь все портфели – эффективные.

При 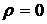получаем дугу параболы на 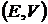и гиперболы н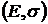а вида:

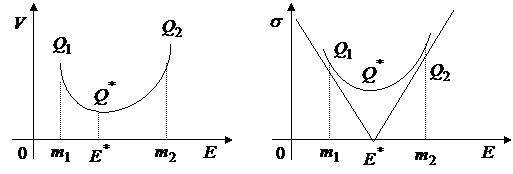Рис.14.

При 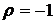получаем:

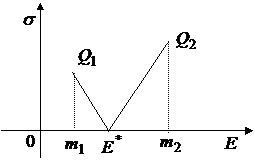Рис.15.

На критериальной плоскости 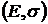можем изобразить теперь критериальные множества, соответствующие различным значениям коэффициента корреляции :

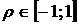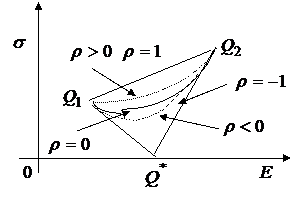Рис.16.

Получили треугольник 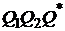, сплошь заполненный дугами гипербол.

Заметим, что портфель 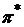с риском, меньшим, чем риск каждого из активов 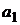и 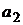, можно получить, если

.

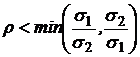В этом случае портфель 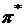будет обязательно лучше портфеля, состоящего из актива с меньшей доходностью.

Таким образом, можно сделать вывод о том, что наличие отрицательной корреляции 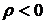между активами, позволяет существенно снизить риск портфеля 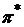, то есть портфель 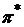будет обязательно лучше одного из них и не хуже другого. Для нахождения такого портфеля необходимо решить задачу минимизации 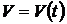при условии 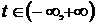для модели Блека, и 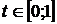для модели Марковица. Найденное значение 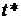дает оптимальный портфель 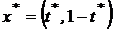и его оценку .

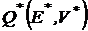МОДЕЛИ С БЕЗРИСКОВЫМ АКТИВОМ

Здесь речь идет о модели, в которой предусматривается наличие безрискового актива.

Пусть, например, актив 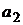будет безрисковым, то есть, 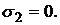Тогда ковариационная матрица 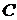примет вид

.

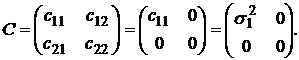Будем рассматривать два конкретных вида портфелей: с возможными короткими позициями (модель Блека) и стандартные, без коротких позиций (модель Марковица).

Модель Блека

Учитывая, что 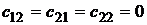, из уравнений (6) и (7) можем получить

,

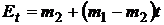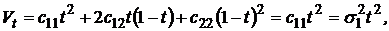
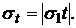
Безрисковому портфелю соответствует значение параметра 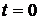, то есть такой портфель состоит только из безрискового актива 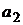с оценкой 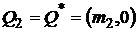. Критериальное множество на плоскости 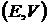имеет вид параболы

,

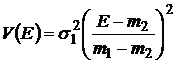а на плоскости 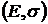представляет собой пару лучей с вершиной в точке :

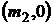Рис.17.

Модель Марковица

В этом случае, параметр 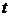принимает значения только из отрезка [0;1], поэтому критериальное множество представляет собой соответствующее подмножество для модели Блека вида:

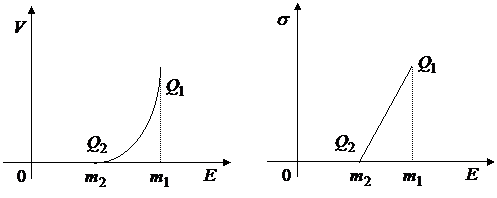Рис.18.

То есть, критериальное множество представляет собой дугу параболы 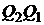на плоскости 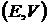или отрезок прямой 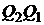на плоскости .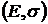