Геометрия множества эффективных портфелей

ГЕОМЕТРИЯ МНОЖЕСТВА ЭФФЕКТИВНЫХ ПОРТФЕЛЕЙ

ПОСТАНОВКА ЗАДАЧИ О ВЫБОРЕ ОПТИМАЛЬНОГО

ПОРТФЕЛЯ

Инвестор при выборе оптимального портфеля использует два критерия: среднюю (ожидаемую) доходность портфеля:

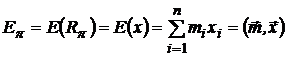, (1)

и риск портфеля, определяемый как дисперсия:

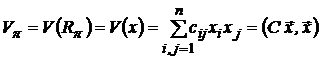, (2)

или как стандартное отклонение:

.

Кроме того, в конкретных задачах могут быть заданы некоторые финансовые условия, ограничивающие вид выбираемых портфелей: исключены или ограничены короткие позиции, ограничены величины отдельных позиций и т.д. В целом, эти ограничения определяют класс допустимых портфелей:

. (3)

Наличие двух критериев 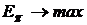и 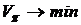значительно осложняет выбор оптимального портфеля, так как улучшение значения одного критерия, как правило ухудшает значение другого критерия. Поэтому различают несколько подходов к решению задачи выбора оптимального портфеля.

1. Отказываются от нахождения портфеля наилучшего по всем критериям, так как такого решения может просто не существовать. Вместо этого ищут так называемые эффективные решения. Решение является эффективным, если любое другое решение, лучшее по одному критерию, будет обязательно хуже по другому критерию. Такие портфели называют также оптимальными по Парето.

2. Выбирается главный критерий, по которому и будет производиться оптимизация, а остальные критерии задают так называемые критериальные ограничения. Так, считая главным критерием доходность, можно поставить задачу максимизации доходности, при условии, что риск не превысит некоторого заданного уровня:

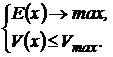
Если же главным критерием считать риск, то можно поставить задачу минимизации риска портфеля при некотором минимально допустимом уровне доходности:

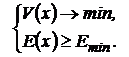
3. Задается некоторый суперкритерий в виде однозначной функции от всех критериев. В задаче выбора оптимального портфеля в качестве такого критерия используют уровневую функцию полезности Неймана-Моргенштерна вида:

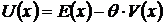, (4)

где - некоторое неопределенное число.

В этом случае увеличение доходности при неизменном риске, или уменьшение риска при неизменном доходе приводит к увеличению полезности. Следовательно, при таком подходе решается задача максимизации квадратичной функции 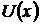при ограничениях (3):

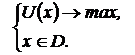
Здесь параметр 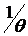характеризует склонность инвестора к риску. Чем больше 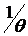, тем выше склонность инвестора к риску и наоборот.

Таким образом, оптимальным можно считать такой портфель, который в наибольшей степени удовлетворяет предпочтениям инвестора по отношению к доходности и риску.

КРИТЕРИАЛЬНОЕ МНОЖЕСТВО

МОДЕЛЬ БЛЕКА ДЛЯ ДВУХ АКТИВОВ

Критериальное множество

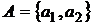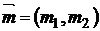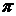Рассмотрим рынок из двух активов с параметрами и . Портфель описывается парой 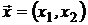с основным ограничением 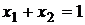. Представим последнее условие в параметрическом виде:

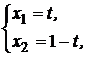
где 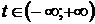. Тогда портфель 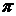будет описываться парой:

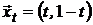. (5)

Вычислим доходность 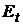и риск 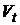такого портфеля:

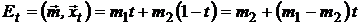; (6)

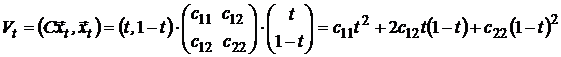. (7)

Учитывая, что 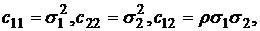равенство (7) можно переписать в виде:

(7¢)

Из последнего равенства следует, что риск 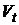портфеля зависит не только от рисков активов 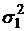и 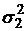, но и от коэффициента корреляции .

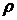Равенства (6) и (7) определяют на критериальной плоскости 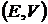критериальное множество , которое, как легко увидеть, представляет собой линию второго порядка вида 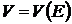. В этом можно убедиться, выразив 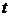из уравнения (6) и подставив полученное выражение в (7¢). Однако при этом получается достаточно громоздкое выражение, поэтому проведем предварительно исследование этой линии при различных значениях коэффициента корреляции .

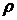3.2. Коэффициент корреляции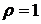

В этом случае, уравнение (7’) примет вид:

.

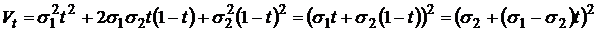Подставив в последнее равенство параметр t из равенства (6):

,

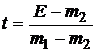получим

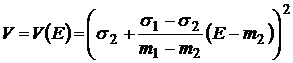. (8)

То есть, в невырожденном случае 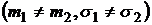, критериальное множество представляет собой параболу на критериальной плоскости :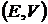

Рис.7.

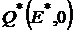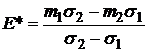Эта парабола имеет вершину , с нулевым риском и доходностью (следует из равенства V(E)=0), и такой оценке соответствует портфель:

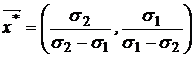. (9)

Видно, что полное устранение риска в этом случае достигается только с использованием коротких позиций, так как одно из чисел 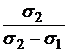и 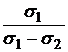обязательно отрицательно.

С другой стороны, к полному устранению риска нужно подходить осторожно, так как, например, в случае

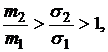
получаем, что доходность такого портфеля будет отрицательной 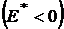, поэтому такое устранение риска является бессмысленным.

Если же риск измерять не дисперсией, а стандартным отклонением 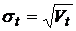, то из формулы (8) получаем:

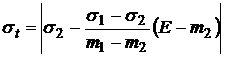. (10)

В этом случае, критериальное множество представляет собой пару лучей с вершиной в точке :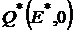

Рис.8.

Таким образом, в случае 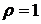минимальная граница совпадает с критериальным множеством, а эффективная граница представляет собой «правую ветвь» параболы на 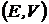, или «правый луч» на плоскости .

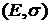3.3. Коэффициент корреляции .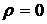

В этом случае оценки портфелей имеют вид:

,

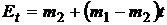. (11)

Выражая t через E_t и подставляя в 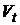, получим параболу с вершиной Q^*. Найдем координаты вершины этой параболы из условия , а именно

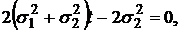
или

.

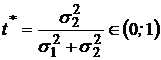Тогда

,

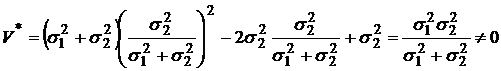и

.

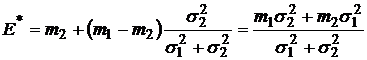Таким образом, хотя , то есть риск портфеля 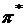меньше риска каждого из активов, но полностью устранить риск нельзя.

Критериальное множество (парабола) в этом случае имеет вид:

Рис.9.

На плоскости 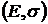получаем кривую

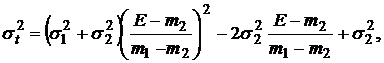(11')

которая представляет собой «верхнюю» ветвь гиперболы.

Рис.10.

Отметим, что здесь .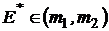

Как и в §3.2. минимальная граница совпадает с самим критериальным множеством, а эффективная граница – это «правая ветвь» параболы или гиперболы (соответственно).

3.4. Коэффициент корреляции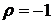

В этом случае

,

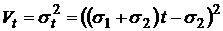, (12)

или

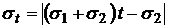. (12')

Это означает, что на плоскости (E,V) критериальное множество будет параболой с вершиной 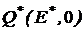, в которой 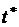вычисляется из условия

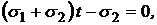
или

.

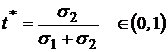Тогда

,

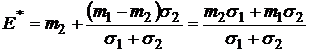и парабола имеет вид:

Рис.11.

Здесь 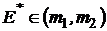и риск можно устранить полностью 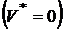только при использовании длинных позиций, так как .

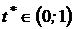На плоскости получаем пару лучей:

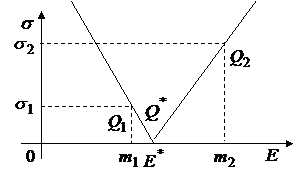Рис.12.

Аналогичный анализ можно провести и для остальных 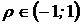. При этом следует, что:

а) полностью устранить риск можно лишь при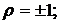

б) в общем случае на плоскости 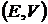критериальное множество будет параболой, а на 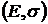- гиперболой;

в) при 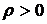вершина 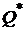будет лежать вне дуги 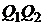, а при 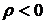- внутри дуги .

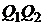Модель Блека

Учитывая, что 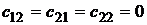, из уравнений (6) и (7) можем получить

,

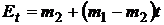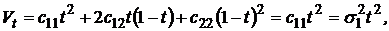
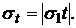
Безрисковому портфелю соответствует значение параметра 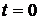, то есть такой портфель состоит только из безрискового актива 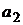с оценкой 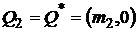. Критериальное множество на плоскости 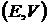имеет вид параболы

,

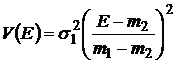а на плоскости 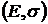представляет собой пару лучей с вершиной в точке :

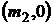Рис.17.

Модель Марковица

В этом случае, параметр 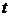принимает значения только из отрезка [0;1], поэтому критериальное множество представляет собой соответствующее подмножество для модели Блека вида:

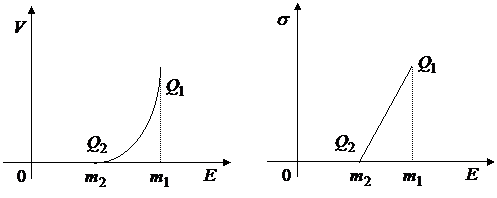Рис.18.

То есть, критериальное множество представляет собой дугу параболы на плоскости или отрезок прямой 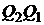на плоскости .

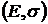МОДЕЛИ С ТРЕМЯ АКТИВАМИ

Для двумерных моделей, рассмотренных выше, критериальные множества представляли собой линии на плоскости, и граница критериального множества совпадала с самим множеством. Для моделей с числом активов более двух критериальное множество будет содержать и внутренние точки. Рассмотрим для примера модель Марковица с тремя активами, а именно

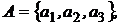
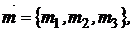
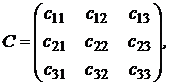
Каждый портфель 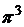описывается вектором:

,

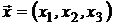с ограничением , .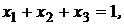

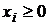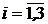Пусть 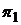, , 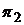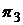- портфели, составленные только из одного актива с векторами:

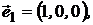
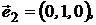
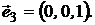
а 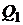, , 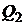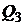- соответственно – оценки этих портфелей на критериальной плоскости.

Класс всех трехмерных портфелей модели Марковица представляет собой двумерный комплекс 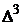в трехмерном пространстве:

Рис.21.

с вершинами в единичных точках. А образы отрезков 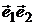, , 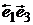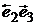на критериальной плоскости 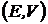будут дугами парабол 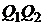, , 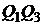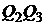соответственно; а критериальное множество будет представлять собой криволинейный треугольник.

Рис.22.

Если же эти дуги пересекаются, как на следующем рисунке, то, вроде бы, получается критериальное множество, состоящее из трех криволинейных треугольников.

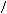Рис.23.

Однако мы уже знаем, что минимальная граница критериального множества должна быть выпуклой линией. Поэтому, взяв, например, оценки портфеле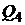й и 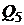для достижения линейной комбинации этих портфелей, получим дугу параболы 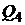и 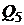. Повторив многократно этот процесс с различными оценками трехмерных портфелей, придем к критериальному множеству в виде одного криволинейного треугольника, только при этом границы будут состоять не из одной параболы, а из кусков парабол.

Возможны и другие виды критериального множества, например,

Рис.24.

Или, если в портфель входит безрисковый актив (пусть это портфель с оценкой 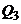), то критериальное множество будет иметь вид:

Рис.25.

то есть она будет касаться оси абсцисс.

На критериальной плоскости 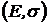критериальное множество строится из кусков гипербол или прямолинейных отрезков. Например, если в портфель входит безрисковый актив с оценкой , то типичное критериальное множество будет иметь вид

Рис.26.

Отметим, что до сих пор мы строили критериальное множество на критериальной плоскости, в которой (для удобства) доходность отмечали на оси абсцисс, а риск на оси ординат. Однако в финансовой литературе действует и обратное правило, согласно которому типичные критериальные множества для моделей Блека и Марковица изображаются следующим образом:

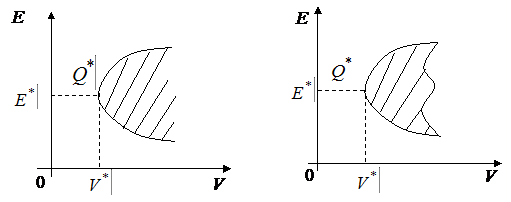Рис.27.

ГЕОМЕТРИЯ МНОЖЕСТВА ЭФФЕКТИВНЫХ ПОРТФЕЛЕЙ