Расчет методом контурных токов

4.1.1 Изображение расчётной схемы замещения электрической цепи для выбранного варианта

Пусть в первой и третьей ветвях содержатся индуктивности, в четвертой и пятой – емкости, а во второй – сопротивление.

Тогда расчетная схема замещения цепи будет иметь вид, изображенный на рисунке 2.

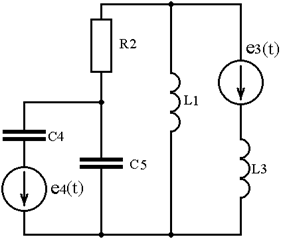
Рисунок 2 - Расчётная схема замещения электрической цепи

4.1.2 Изображение комплексной схемы замещения

Комплексная схема замещения цепи изображена на рисунке 3.

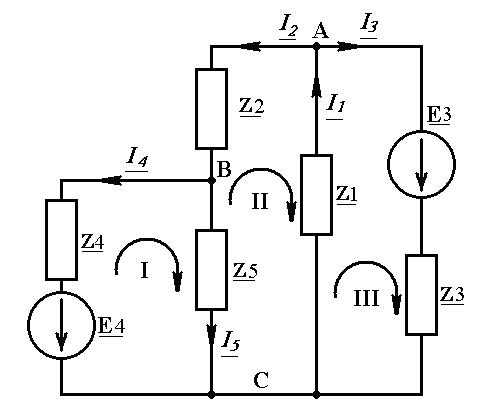
Рисунок 3 – Комплексная схема замещения электрической цепи

Цепь имеет 3 узла (A,B,C) и 5 ветвей. Следовательно, при использовании метода уравнений Кирхгофа необходимо решать систему из 7 уравнений.

Метод контурных токов позволяет решать систему из 3 уравнений, так как в цепи 3 независимых контура.

4.1.3 Выбор положительных направлений токов в ветвях

Условные положительные направления токов в ветвях выбираются произвольно. Выберем их так, как указано на рисунке 3.

4.1.4 Выбор направления обхода и обозначение независимых контуров

Контурные токи обозначим также произвольно, например, по часовой стрелке, как на рисунке 3. Положительные направления обхода контуров выберем совпадающим с направлениями контурных токов.

4.1.5 Запись системы контурных уравнений для расчета контурных токов в общем виде

Составим систему контурных уравнений для контурных токов в общем виде

,

,

,

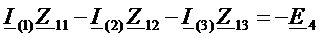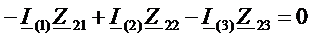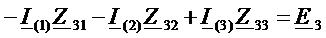где 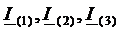- комплексные контурные токи;

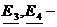комплексные ЭДС;

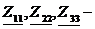собственные комплексные сопротивления контуров;

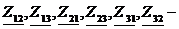взаимные комплексные сопротивления контуров.

Здесь ,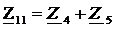

,

,

,

,

.

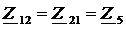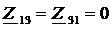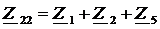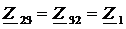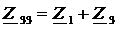4.1.6 Расчет сопротивлений элементов схемы на указанной частоте

,

,

,

,

.

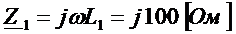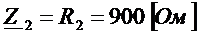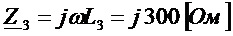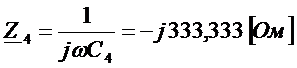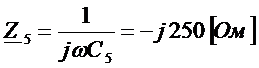4.1.7 Расчет собственных и взаимных сопротивлений

,

,

,

,

.

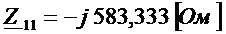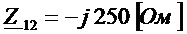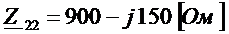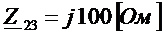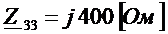4.1.8 Расчет контурных токов

Систему уравнений будем решать методом Крамера. Найдем сначала определитель системы

.

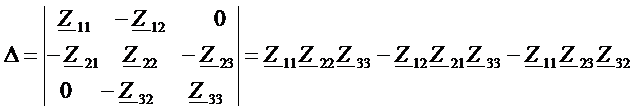Подставляя значения, получим

.

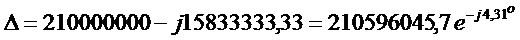Определитель для тока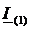

.

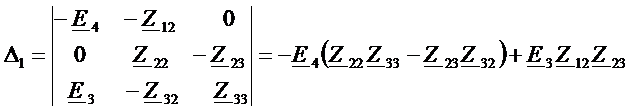После подстановки значений имеем

.

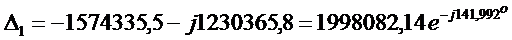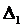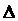Разделив на , получим значение контурного тока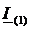

.

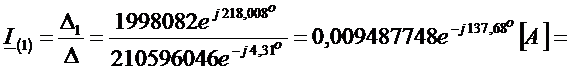
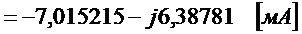Определитель для тока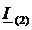

.

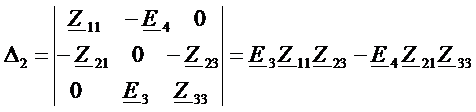Для заданных значений имеем

.

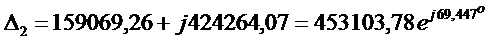Определим ток контурный ток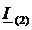

.

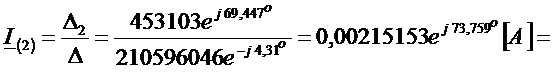
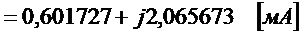Определитель для тока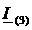

.

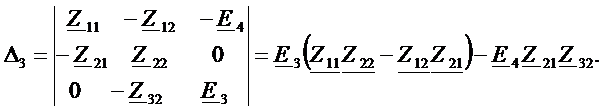Подставляя значения, получим

.

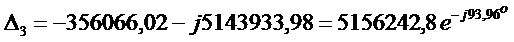Отсюда контурный ток 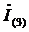равен

.

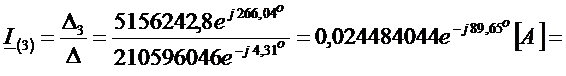
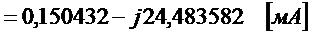4.1.9 Расчет токов в ветвях и напряжений на элементах.

В соответствии с обозначениями рисунка 3 получаем

,

,

,

,

,

,

,

,

,

.

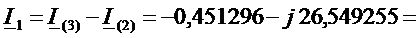
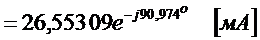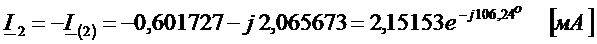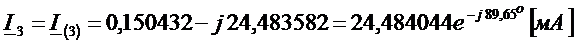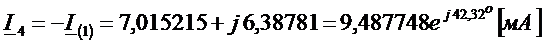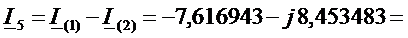
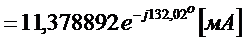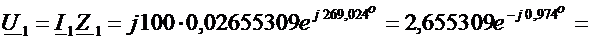
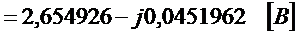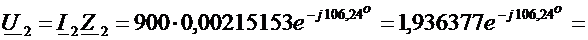
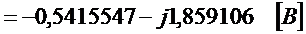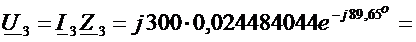
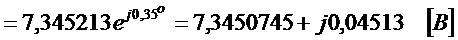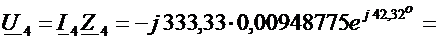
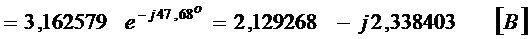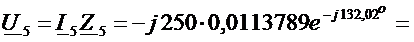
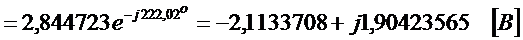4.1.10 Проверка правильности решения задачи на основе выполнения законов Кирхгофа

Проверим выполнение 1 закона Кирхгофа.

Для узла А:

.

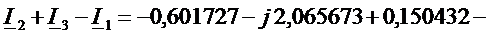
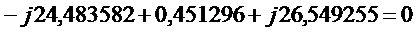Для узла В:

.

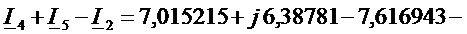
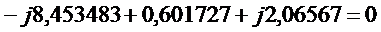Следовательно, первый закон Кирхгофа выполняется.

Проверим выполнение 2 закона Кирхгофа.

Для контура 1:

.

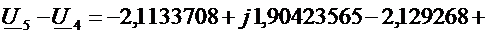
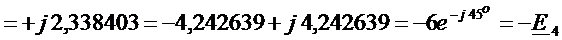Для контура 2:

.

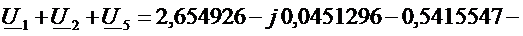
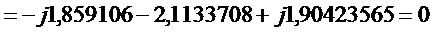Для контура 3:

.

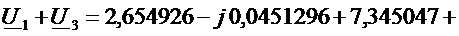
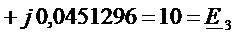Таким образом, можно утверждать, что задача решена верно, поскольку законы Кирхгофа выполняются.

4.1.11 Запись результатов в виде мгновенных значений

,

,

,

,

,

,

,

,

,

.
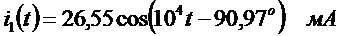
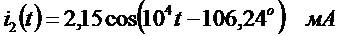
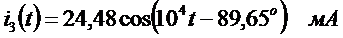
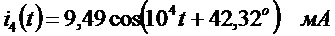
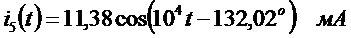
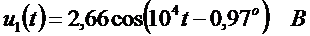
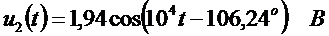
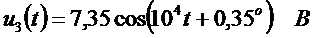
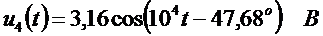
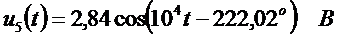