Разложение полинома на сомножители

Теперь мы можем окончательно решить вопрос о разложении полинома на сомножители. Рассмотрим полином 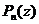. Пусть он имеет действительныекорни 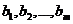с кратностями 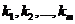соответственно. Далее, пусть он имеет пары комплексно сопряженныхкорней 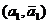, , 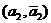… , 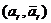с кратностями 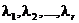соответственно. Заметим, что при этом выполняется условие

.

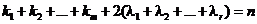Откажемся от комплексной переменной z, и будем рассматривать наш полином как функцию действительнойпеременной х. Тогда имеет место разложение

.

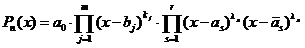Рассмотрим пару 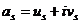, 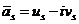. Для нее имеем

.

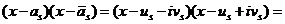
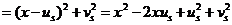Обозначим 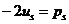, 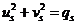. Тогда

.

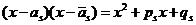Заметим, что в этом случае должно выполняться условие .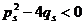

Тогда полином 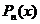можно представить в виде

. (*)

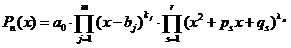Сомножитель 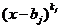соответствует действительному корню 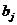кратности 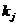; сомножитель 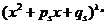- паре комплексно сопряженных корней кратности .

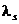Это разложение полинома на сомножители является для дальнейшего основным. Всюду далее будет предполагаться, что все корни полинома найдены и он разложен на сомножители вида (*).

Разложение рациональных дробей на простейшие

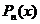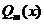Пусть и есть полиномы действительной переменной х. Функция вида 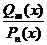называется дробно рациональной функцией,или, короче, рациональной дробью. Если 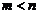, то рациональная дробь называется правильной.

Если 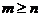, то можно всегда поделить столбиком и представить рациональную дробь в виде

.

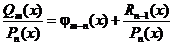Теорема 1. Пусть 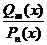- правильная рациональная дробь и b есть действительный корень полинома 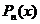кратности k, то есть 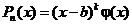, 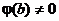. Тогда имеет место разложение

,

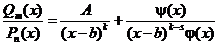где 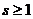, а 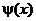- полином такой степени, что второе слагаемое есть правильная рациональная дробь.

Доказательство.

Возьмем 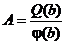и рассмотрим разность

.

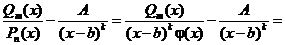
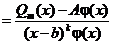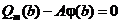, то есть b есть корень полинома 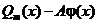. Пусть его кратность равна s. Тогда

,

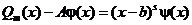и

,

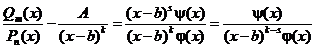что и требовалось доказать. <

Следствие.

Продолжая разложение дальше, получим

.

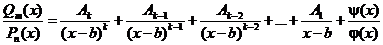Некоторыеиз 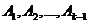могут быть равны нулю, но .

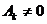Теорема 2. Пусть есть правильная рациональная дробь иb есть комплексный корень полинома 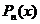кратности l, то есть 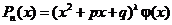. Тогда имеет место разложение

,

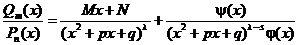где 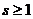, а 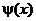- полином такой степени, что второе слагаемое есть правильная рациональная дробь.

Доказательство.

Рассмотрим

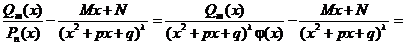
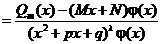
и постараемся подобрать М и N так, чтобы выполнилось условие .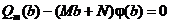

Так как b есть комплексный корень,то 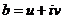и 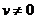. Тогда из нашего условия получим

.

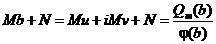Приравнивая мнимые части этих выражений, получим

,

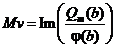откуда однозначно определяется М

.

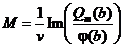Приравнивая действительные части этих выражений, получим

,

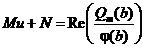откуда, зная М, можно однозначно определить и N:

.

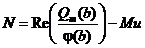Таким образом, М и N определяются однозначно.

Но теперь у полинома 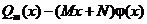будет пара комплексно сопряженных корней b и 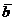некоторой кратности s. Поэтому

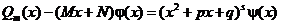
и мы получим

,

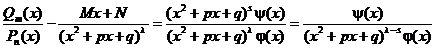что и требовалось доказать. <

Следствие.

Продолжая разложение дальше, получим

.

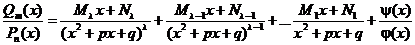Опять таки, некоторыеиз 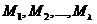и 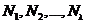могут бытьравны нулю.

Общий вид разложения.

Пусть 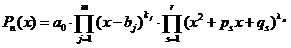и 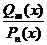есть правильная рациональная дробь. Тогда имеет место разложение

.

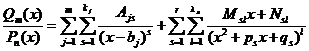Это представление называется разложением правильной рациональной дроби на простейшие.

Заметим в заключение, что некоторыеиз коэффициентов 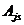, 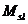и 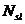могут бытьравны нулю.