Получение математической модели ОУ в форме передаточных функций по управляющему и возмущающему каналам

КУРСОВАЯ РАБОТА

	Теория автоматического управления

По дисциплине:

(наименование учебной дисциплины согласно учебному плану)

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

	Синтез комбинированной системы управления

Тема:______________________________________________________

Выполнил: студентгр.____________ Демонов А.С.

^{(подпись) (Ф.И.О.)}

Дата: __________

Оценка: _________

	доцент		/Стороженко С.В./

ПРОВЕРИЛ:

^{(должность) (подпись) (Ф.И.О.)}

Санкт-Петербург

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

Национальный минерально-сырьевой университет «Горный»

УТВЕРЖДАЮ

Заведующий кафедрой

_______________________

"____"____________201_ г.

Кафедра Э.Э.Э.

КУРСОВАЯ РАБОТА

По дисциплине: Теория автоматического управления

ЗАДАНИЕ

Студенту группы: Эрн-09-2/ДемоновА.С./ .0 /

^{(шифр группы) (Ф.И.О.)}

1. Тема работы: Синтез комбинированной системы управления.

2.Исходные данные к проекту: Вариант № 1. Синтез комбинированной системы управления техническим объектом, заданным экспериментальными переходными характеристиками по управляющему и возмущающему каналам.

3.Содержание пояснительной записки: Получение математической модели объекта управления (ОУ) в форме передаточных функций по управляющему и возмущающему воздействиям, выбор ПИ-алгоритма управления, расчёт параметров ПИ-регулятора по параметрам объекта по регулирующему каналу графоаналитическим методом, получение передаточной функции физически реализуемого компенсатора, построение переходных процессов в системе по задающему и возмущающему воздействиям (переходной процесс по возмущению построить с компенсатором и без него), определение показателей качества, определение параметров САУ для перехода к НЦУ, построение САУ с использованием методов нечёткой логики (Fuzzy-логики).

4. Содержание графической части: Переходные характеристики ОУ по управляющему и возмущающему воздействию. Структурная схема САУ с указанием найденных передаточных функций. Графический расчет параметров регулятора Р. Переходные процессы в САУ. Структурная схема НЦУ. Структурная схема нечёткой системы. Графический расчет нечеткого регулятора.

5. Срок сдачи законченного проекта: 20 декабря 2012 г.

доцент

Стороженко С.В.

Руководитель работы: _________ ________________ /________________/

^{(должность) (подпись) (Ф.И.О.)}

Дата выдачи задания: 20 сентября 2012 г.

Аннотация

В работе рассматриваются вопросы, связанные с синтезом САУ, с типовым алгоритмом управления для технологических объектов. Даются рекомендации по применению полученных результатов к системам с непосредственным цифровым управлением (НЦУ), рассматриваются возможности применения методов нечеткой логики (фаззи-логики) при синтезе систем автоматического управления.

Annotation

The questions, related to the SAU synthesis with the model algorithm of management for the technological objects set by experimental transitional descriptions, are here examined. Recommendations on application of the got results to the systems with the direct digital management are given (NTSU). Possibilities of application of methods of fuzzy-logic at the synthesis of the systems of automatic control are examined.

Содержание

Введение. 5

Исходные данные. 7

1. Получение математической модели ОУ в форме передаточных функций по управляющему и возмущающему каналам.. 8

1.1. Аппроксимация переходной характеристики объекта по управляющему каналу. 8

1.2. Аппроксимация переходной характеристики объекта по возмущающему каналу. 13

2. Выбор ПИ-алгоритма управления. 16

3.Расчет параметров ПИ-регулятора по параметрам объекта по регулирующему каналу графоаналитическим методом.. 19

4. Построение переходных процессов в системе по задающему воздействию при выбранных параметрах регулятора. 23

5. Получение передаточной функции физически реализуемого компенсатора, обеспечивающего наилучшую компенсацию возмущения. 25

6. Определение показателей качества в системе по возмущающему воздействию с компенсатором и без него 27

7.Составление структурной схемы САУ с НЦУ и запись алгоритма цифрового управления. 32

7.1. Определение Т₀ 33

7.2. Составление структурной схемы САУ с НЦУ.. 33

7.3. Запись алгоритма цифрового управления. 34

8. Построение САУ с использованием методов нечёткой логики. 38

8.1. Структурная схема комбинированной САУ с нечётким компенсатором.. 38

8.2. Расчёт управляющего воздействия нечёткого компенсатора. 39

Заключение. 41

Список используемой литературы.. 42

Приложение. 43

Введение

Промышленные объекты управления (ОУ), как правило, представляют собой сложные агрегаты со многими входными и выходными величинами, характеризующими технологический процесс. Зависимости выходных величин от входных, как правило, нелинейные, и изменение одной из них приводит к изменению других. Таким образом, создается сложная система взаимозависимостей, которую трудно, а подчас и невозможно строго математически описать.

Большинство промышленных объектов описываются передаточными функциями, имеющими большое время запаздывания τ_а и большие постоянные времени Т_а.

Известно, что чем больше время запаздывания, тем труднее управлять объектом. Качество регулирования в будущей САУ зависит от отношения τ_а/ Т_а. Чем оно больше, тем труднее управлять, поэтому при описании объекта (τ_а/ Т_а)≤1.

Для большинства объектов τ_а/ Т_а так велико, что удовлетворяющее нас качество в системе в одноконтурной САУ получить практически невозможно. В этом случае нужно усложнить закон регулирования. На практике идут не на усложнение закона регулирования, а на усложнение структуры САУ.

В настоящее время в практике автоматизации непрерывных производственных процессов применяются следующие виды мно­гоконтурных схем: каскадные системы, комбинированные САУ и многосвязные системы. Расчет оптимальных параметров управ­ляющих устройств перечисленных многоконтурных систем явля­ется довольно сложной задачей. Для упрощения на практике опре­деляют лишь приближенные значения этих параметров.

Методика приближенных расчетов основана на предполо­жении о возможности расчета отдельных контуров системы неза­висимо друг от друга. Для этих целей, исходная структурная схема управления подвергается различным структурным преобразовани­ям с тем, чтобы выделить отдельные контуры с различными часто­тами и рассчитывать их обычными методами независимо друг от друга, тем самым получают более сложный алгоритм управления комбинацией ограниченного числа типовых П -, ПИ-, ПИД зако­нов регулирования.

Комбинированные системы регулирования рекомендуется строить, если на систему действу­ют значительные внешние возмущения и если представляется возможность выделить и измерить главные из них.

Система содержит минимум два контура регу­лирования. Разомкнутый контур с преобразователем служит для компен­сации основного возмуще­ния (или возмущений) f; замкнутый контур с регулятором окончательно корректирует процесс, отрабатывая ошибки компенсации первого контура и другие неучтенные возмущения, многие из которых практически не могут быть контролируемыми (помехи). Комби­нированное управление сочетает в себе два принципа регулиро­вания: регулирование «по возмущению» и регулирование «по от­клонению».

Исходные данные

Необходимо выполнить синтез комбинированной системы управления (рис. 1) техническим объектом, заданным экспериментальными переходными характеристиками по управляющему и возмущающему каналам, приведёнными в таблице (1).

Таблица 1

t, с
Канал f-y			0,01	0,02	0,04	0,09	0,14	0,19	0,21	0,23	0,25	0,27	0,29	0,31	0,32	0,32
Канал u-y		0,01	0,07	0,32	0,45	0,55	0,58	0,6	0,62	0,64	0,65	0,65	0,65	0,65	0,65	0,65

Построенные по экспериментальным данным (таблица 1) переходные характеристики по управляющему и возмущающему каналам представлены на рис.2 и рис.5 соответственно.

Рис.1. Заданная комбинированная САУ

Рис. 4 Переходные характеристики моделей объекта управления по управляющему каналу и заданная экспериментально переходная характеристика по управляющему каналу.

1 -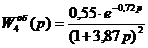

2 -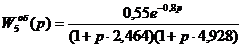

3 -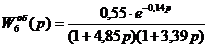

4 - заданная экспериментально переходная характеристика по управляющему каналу

Рис. 6 Переходные характеристики моделей объекта управления по возмущающему каналу и заданная экспериментально переходная характеристика по возмущающему каналу.

1 -

2 -

3 -

4 - заданная экспериментально переходная характеристика по управляющему каналу

Рис.7. Определение центра и радиуса окружности, соответствующей заданному показателю колебательности М

Если же W_раз(jw) касается указанной окружности, то это означает, что САУ находится на границе заданного запаса устойчивости.

На практике чаще всего принимают . При этом в САУ перерегулирование g £ 40%, максимальное отклонение регулируемого параметра при внутренних возмущениях (возмущениях по регулирующему воздействию) не превышает 10%.

Рис. 9 Переходный процесс САУ по задающему воздействию при выбранных параметрах регулятора

С компенсатором

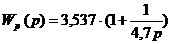
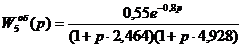
Расчет и построение данного переходного процесса выполняется в программе «СС», он показан на рис.10.

Определяем показатели качества системы:

1. Статическая ошибка:

.

2. Время регулирования:

3. Перерегулирование:

Качество управления считается удовлетворительным, если перерегулирование не превышает 30-40%.

4. Колебательность:

Рис. 10, Переходный процесс САУ по возмущающему воздействию с компенсатором

Без компенсатора

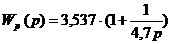
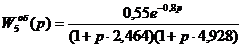
Расчет и построение данного переходного процесса выполняется в программе «СС», он показан на рис.11.

Определяем показатели качества системы:

1. Статическая ошибка:

.

2 . Время регулирования:

3. Перерегулирование:

Качество управления считается удовлетворительным, если перерегулирование не превышает 30-40%.

4. Колебательность:

5. Степень затухания:

Интенсивность затухания колебаний в системе считается удовлетворительной, если .

Рис. 11, Переходный процесс САУ по возмущающему воздействию без компенсатора

Вывод: Оценив переходные процессы по возмущающему воздействию, можно сделать вывод, что построенная система автоматического управления является работоспособной и имеет показатели качества на хорошем уровне.

		Рис.12 Структурная схема комбинированной системы управления

Рис. 13 Структурная схема САУ с НЦУ

Рис.14 Блок-схема работы САУ с НЦУ

Рис. 15. Структурная схема САУ с Fuzzy-регулятором

Fuzzy-регулятор содержит три основных блока: F – блок фаззификации БФ, I – блок нечеткого вывода БНВ (блок принятия решений), D – блок дефаззификации БДФ.

Вся информация о стратегии управления заложена в базе знаний в виде правил условного логического вывода: Если….. тогда… Эти правила получаются за счет тщательного изучения ОУ и цели его управления путем анкетного опроса экспертов (технологи-операторы, специалисты по автоматизации).

Центральным звеном является БНВ, в котором нечеткая информация о возмущении f (его производной) формирует нечеткое множество управления.

Выполняется инференц-процедура, в результате которой объединяются выводы нечетких правил, и результатом этого объединения является усеченное множество управляющих воздействий.

БФ преобразует конкретное измеренное значение возмущения с помощью некоторой функции принадлежности в нечеткое множество. В БДФ происходит обратный процесс.

Заключение

В данной работе выполнен синтез комбинированной САУ техническим объектом, заданным в форме экспериментальных переходных характеристик. Произведен выбор математической модели объекта управления в форме передаточных функций по управляющему и возмущающему каналам, выбран ПИ алгоритм управления и произведен расчет параметров ПИ-регулятора графоаналитическим методом. Рассчитан физически реализуемый компенсатор, обеспечивающий компенсацию возмущений. Построены кривые переходных процессов в системе и определены показатели качества. Осуществлен переход од аналогового (непрерывного) регулятора к НЦУ. Построена САУ с использованием методов нечёткой логики. Рассчитано компенсирующее воздействие нечёткого компенсатора.

Список используемой литературы

1) Лукас В.А. Теория управления техническими системами. Учебное пособие для вузов. 4-е издание. Екатеринбург: издательство УГГУ, 2005г., 677с.

2) Стороженко С.В., Коржев А.А. Теория автоматического управления. Синтез САУ горного и нефтегазового производства. СПБ: издательство СПГГИ(ТУ), 2010г., 58с.

3) Ротач В.Я. Теория автоматического управления технологическими процессами. М.:Энергоатомиздат, 1985г., 386 с.

4) Стальский В.В., Проскуряков Р.М. Нечеткая логика и ее применение в автоматическом регулировании. СПБ.: СПГГИ(ТУ), 1998г., 65 с.

5) Марюта А.Н., Качан Ю.Г. Бунько В.А. Автоматическое управление технологическими процессами обогатительных фабрик. М.: Недра, 1983г., 277 с.

6) Ротач В.Я., Шавров А.В. Бутырев В.Н. Синтез алгоритмов машинного расчета оптимальных параметров систем регулирования. Теплоэнергетика. 1987 г. № 12, с 76-79.

7) Медведев Р.Е., Бондарь Б.Д., Романенко В.Д. АСУ ТП в металлургии. М.: Металлургия, 1987 г., 251 с.

Приложение

Приложение 1

Рис. П1, Графоаналитический метод расчёта ПИ-регулятора

Рис. П2, расчёт управляющего воздействия нечёткого компенсатора

КУРСОВАЯ РАБОТА

	Теория автоматического управления

По дисциплине:

(наименование учебной дисциплины согласно учебному плану)

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

	Синтез комбинированной системы управления

Тема:______________________________________________________

Выполнил: студентгр.____________ Демонов А.С.

^{(подпись) (Ф.И.О.)}

Дата: __________

Оценка: _________

	доцент		/Стороженко С.В./

ПРОВЕРИЛ:

^{(должность) (подпись) (Ф.И.О.)}

Санкт-Петербург

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

Национальный минерально-сырьевой университет «Горный»

УТВЕРЖДАЮ

Заведующий кафедрой

_______________________

"____"____________201_ г.

Кафедра Э.Э.Э.

КУРСОВАЯ РАБОТА

По дисциплине: Теория автоматического управления

ЗАДАНИЕ

Студенту группы: Эрн-09-2/ДемоновА.С./ .0 /

^{(шифр группы) (Ф.И.О.)}

1. Тема работы: Синтез комбинированной системы управления.

2.Исходные данные к проекту: Вариант № 1. Синтез комбинированной системы управления техническим объектом, заданным экспериментальными переходными характеристиками по управляющему и возмущающему каналам.

3.Содержание пояснительной записки: Получение математической модели объекта управления (ОУ) в форме передаточных функций по управляющему и возмущающему воздействиям, выбор ПИ-алгоритма управления, расчёт параметров ПИ-регулятора по параметрам объекта по регулирующему каналу графоаналитическим методом, получение передаточной функции физически реализуемого компенсатора, построение переходных процессов в системе по задающему и возмущающему воздействиям (переходной процесс по возмущению построить с компенсатором и без него), определение показателей качества, определение параметров САУ для перехода к НЦУ, построение САУ с использованием методов нечёткой логики (Fuzzy-логики).

4. Содержание графической части: Переходные характеристики ОУ по управляющему и возмущающему воздействию. Структурная схема САУ с указанием найденных передаточных функций. Графический расчет параметров регулятора Р. Переходные процессы в САУ. Структурная схема НЦУ. Структурная схема нечёткой системы. Графический расчет нечеткого регулятора.

5. Срок сдачи законченного проекта: 20 декабря 2012 г.

доцент

Стороженко С.В.

Руководитель работы: _________ ________________ /________________/

^{(должность) (подпись) (Ф.И.О.)}

Дата выдачи задания: 20 сентября 2012 г.

Аннотация

В работе рассматриваются вопросы, связанные с синтезом САУ, с типовым алгоритмом управления для технологических объектов. Даются рекомендации по применению полученных результатов к системам с непосредственным цифровым управлением (НЦУ), рассматриваются возможности применения методов нечеткой логики (фаззи-логики) при синтезе систем автоматического управления.

Annotation

The questions, related to the SAU synthesis with the model algorithm of management for the technological objects set by experimental transitional descriptions, are here examined. Recommendations on application of the got results to the systems with the direct digital management are given (NTSU). Possibilities of application of methods of fuzzy-logic at the synthesis of the systems of automatic control are examined.

Содержание

Введение. 5

Исходные данные. 7

1. Получение математической модели ОУ в форме передаточных функций по управляющему и возмущающему каналам.. 8

1.1. Аппроксимация переходной характеристики объекта по управляющему каналу. 8

1.2. Аппроксимация переходной характеристики объекта по возмущающему каналу. 13

2. Выбор ПИ-алгоритма управления. 16

3.Расчет параметров ПИ-регулятора по параметрам объекта по регулирующему каналу графоаналитическим методом.. 19

4. Построение переходных процессов в системе по задающему воздействию при выбранных параметрах регулятора. 23

5. Получение передаточной функции физически реализуемого компенсатора, обеспечивающего наилучшую компенсацию возмущения. 25

6. Определение показателей качества в системе по возмущающему воздействию с компенсатором и без него 27

7.Составление структурной схемы САУ с НЦУ и запись алгоритма цифрового управления. 32

7.1. Определение Т₀ 33

7.2. Составление структурной схемы САУ с НЦУ.. 33

7.3. Запись алгоритма цифрового управления. 34

8. Построение САУ с использованием методов нечёткой логики. 38

8.1. Структурная схема комбинированной САУ с нечётким компенсатором.. 38

8.2. Расчёт управляющего воздействия нечёткого компенсатора. 39

Заключение. 41

Список используемой литературы.. 42

Приложение. 43

Введение

Промышленные объекты управления (ОУ), как правило, представляют собой сложные агрегаты со многими входными и выходными величинами, характеризующими технологический процесс. Зависимости выходных величин от входных, как правило, нелинейные, и изменение одной из них приводит к изменению других. Таким образом, создается сложная система взаимозависимостей, которую трудно, а подчас и невозможно строго математически описать.

Большинство промышленных объектов описываются передаточными функциями, имеющими большое время запаздывания τ_а и большие постоянные времени Т_а.

Известно, что чем больше время запаздывания, тем труднее управлять объектом. Качество регулирования в будущей САУ зависит от отношения τ_а/ Т_а. Чем оно больше, тем труднее управлять, поэтому при описании объекта (τ_а/ Т_а)≤1.

Для большинства объектов τ_а/ Т_а так велико, что удовлетворяющее нас качество в системе в одноконтурной САУ получить практически невозможно. В этом случае нужно усложнить закон регулирования. На практике идут не на усложнение закона регулирования, а на усложнение структуры САУ.

В настоящее время в практике автоматизации непрерывных производственных процессов применяются следующие виды мно­гоконтурных схем: каскадные системы, комбинированные САУ и многосвязные системы. Расчет оптимальных параметров управ­ляющих устройств перечисленных многоконтурных систем явля­ется довольно сложной задачей. Для упрощения на практике опре­деляют лишь приближенные значения этих параметров.

Методика приближенных расчетов основана на предполо­жении о возможности расчета отдельных контуров системы неза­висимо друг от друга. Для этих целей, исходная структурная схема управления подвергается различным структурным преобразовани­ям с тем, чтобы выделить отдельные контуры с различными часто­тами и рассчитывать их обычными методами независимо друг от друга, тем самым получают более сложный алгоритм управления комбинацией ограниченного числа типовых П -, ПИ-, ПИД зако­нов регулирования.

Комбинированные системы регулирования рекомендуется строить, если на систему действу­ют значительные внешние возмущения и если представляется возможность выделить и измерить главные из них.

Система содержит минимум два контура регу­лирования. Разомкнутый контур с преобразователем служит для компен­сации основного возмуще­ния (или возмущений) f; замкнутый контур с регулятором окончательно корректирует процесс, отрабатывая ошибки компенсации первого контура и другие неучтенные возмущения, многие из которых практически не могут быть контролируемыми (помехи). Комби­нированное управление сочетает в себе два принципа регулиро­вания: регулирование «по возмущению» и регулирование «по от­клонению».

Исходные данные

Необходимо выполнить синтез комбинированной системы управления (рис. 1) техническим объектом, заданным экспериментальными переходными характеристиками по управляющему и возмущающему каналам, приведёнными в таблице (1).

Таблица 1

t, с
Канал f-y			0,01	0,02	0,04	0,09	0,14	0,19	0,21	0,23	0,25	0,27	0,29	0,31	0,32	0,32
Канал u-y		0,01	0,07	0,32	0,45	0,55	0,58	0,6	0,62	0,64	0,65	0,65	0,65	0,65	0,65	0,65

Построенные по экспериментальным данным (таблица 1) переходные характеристики по управляющему и возмущающему каналам представлены на рис.2 и рис.5 соответственно.

Рис.1. Заданная комбинированная САУ

Получение математической модели ОУ в форме передаточных функций по управляющему и возмущающему каналам