Экспертные оценки и модели бинарного выбора

ГЛАВА 3.

ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ

ЭКСПЕРТНЫХ ПРЕДПОЧТЕНИЙ

Р и с. 3.1. Изменение плотности вероятности

ГЛАВА 3.

ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ

ЭКСПЕРТНЫХ ПРЕДПОЧТЕНИЙ

Экспертные оценки и модели бинарного выбора

3.1.1. Концептуальные основы моделирования экспертных предпочтений. В предыдущих параграфах, достаточно подробно изложен математический аппарат, применяемый в настоящее время и не без успеха в различных схемах получения и обработки экспертной информации, используемой в задачах обоснования управленческих решений. И все же, во всех этих схемах, несмотря на их разнообразие, по преимуществу используются методы из одного и того же выше описанного набора. К этому набору можно добавить балльное оценивание и простое ранжирование, которые в силу своей распространенности и того, что не приводят к получению более надежных оценок, чем метод парных сравнений, не рассматривались среди выше изложенных. Можно вспомнить и медиану Кемени, процедура нахождения которой достаточно сложна и поэтому редко используется в практике получения групповых оценок. Однако в каком бы составе мы не рассматривали эти методы, их главная особенность в том, что для числового представления получаемых результатов в основном используются номинальные и ранговые шкалы. Этим и объясняется, на наш взгляд, тот консерватизм, который утвердился в отношении методов обработки экспертной информации. Его природа очевидна: низкая разрешающая способность экспертов, которая служит непреодолимым барьером для повышения точности экспертных оценок. Возникает естественный вопрос: «Какой смысл в разработке новых подходов и более точных методов, если они из-за указанного барьера не приводят к уточнению финальных результатов?» Трудно возразить этому тезису. И все же смысл есть. Он появляется в тех случаях, когда меняется привычное представление о сути решаемых задач.

В качестве примера, демонстрирующего новый взгляд на обработку экспертной информации, рассмотрим в фокусе этого взгляда задачу ранжирования показателей по их степени влияния на возможность появления какого-либо события. Эта задача является одной из наиболее распространенных в практике экспертного оценивания. Ее решение можно получить с помощью любого из выше рассмотренных методов. Однако, несмотря на многообразие методов, суть подхода, реализуемого в этих методах, одна – непосредственное оценивание показателей. Наряду с простотой реализации этот подход имеет и ряд недостатков. Очевидно, что его применение имеет смысл только в линейном случае, когда степень влияния не зависит от структуры оцениваемого набора показателей.

В реальных ситуациях все гораздо сложней. Представление о линейном взаимодействии скорее абстракция, помогающая упростить задачу, сделав ее всегда решаемой, но с некоторой ошибкой, которой можно пренебречь. Логика получения результатов по такой схеме оценивания без учета совместных эффектов вполне объяснима. Решение ищется для конкретной ситуации с фиксированной структурой показателей, которая хотя и не указывается в задании эксперту, но, как правило, присутствует в его представлениях о решаемой задаче. Но как только структура начинает изменяться, сразу же появляются неучтенные эффекты взаимодействия и надежность экспертных оценок резко снижается. Поэтому непосредственное оценивание показателей, с предполагаемой линейной структурой взаимосвязей, необходимо заменить более сложным, основанным на модельном представлении структуры, но без усложнения самой процедуры опроса экспертов. При этом модель, отражающая взаимосвязь между возможностью появления интересующего нас события и набором оцениваемых показателей, должна быть, по всей вероятности, нелинейной и, кроме того, эконометрической, так как интерес вызывает не только механизм взаимодействия, но и количественная оценка силы этого взаимодействия, а также желание заменить повторные экспертные опросы прогнозными оценками. Последнее особенно важно. Именно этой возможностью не обладают ранее рассмотренные методы.

Таким образом, смысл рассматриваемого здесь подхода в том, чтобы экспертную информацию использовать для построения модели, а не для получения самих оценок. Возникает естественный вопрос: «Каким образом экспертная информации может использоваться для этих целей?» По всей видимости, можно предложить несколько подходов, обеспечивающих реализацию обсуждаемой здесь идеи. Наше предложение заключается в том, чтобы интуицию и знания экспертов применить для формирования специального набора данных псевдовыборки, по данным которой оцениваются коэффициенты модели, имеющей, в отличие от непосредственных экспертных оценок, многоплановое применение: анализ, оценка значимости факторов, прогноз ожидаемых событий и т.п. Естественно, это значительно расширяет область практического использования экспертных решений.

Реализация данного подхода предполагает введение бинарной переменной со следующим смыслом:

.

Будем считать, что значение этой переменной, характеризующей появление интересующего нас события, зависит от оцениваемого нами набора показателей и существует некоторое множество различных вариантов этих наборов , отличающихся друг от друга всеми или некоторыми своими компонентами (оцениваемыми показателями). Предполагается, что у каждого эксперта есть представление о том, при реализации каких вариантов ожидаемое событие будет иметь место, а при реализации каких – нет. Математически это предположение записывается в виде зависимости

, (3.1)

где

– ожидаемое значение бинарной зависимой переменной, которое - ый эксперт связывает с 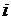- ым набором оцениваемых показателей;

– индексная функция, т.е. функция, принимающая всего два значения 0 и 1;

– ошибка, которую может допустить - ый эксперт, оценивая влияние 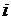-го набора на появление ожидаемого события ( – случайная переменная со значениями в номинальной шкале: 1, 0, -1).

Теперь становится понятной реализация основанной на модельном подходе идеи получения экспертных решений. Сначала в результате целевого опроса экспертов формируется псевдовыборка, объединяющая в себе субъективные мнения по поводу интересующих нас закономерностей, предпочтений, рейтингов, прогнозных оценок и т.п. Затем по данным псевдовыборки строится регрессионная зависимость (3.1), связывающая субъективные мнения с одновременным их усреднением в единую формализованную зависимость. Построенная таким образом модель, по сути, является концентрированным выражением обобщенного мнения экспертов по изучаемой проблеме и может использоваться для анализа и получения всевозможных оценок.

Модель в качестве результата опроса, а не разовые экспертные оценки, является главной особенностью данного подхода. Благодаря этой особенности удается получить прогнозные оценки экспертных суждений, т.е. оценки субъективного характера относительно тех событий или объектов, о которых эксперты не знали или не имели представления в момент формирования псевдовыборки.

Практическая реализация этой процедуры требует рассмотрения целого ряда довольно сложных вопросов:

Как построить регрессию на бинарную переменную?

Какими способами эксперты должны формировать выборочную совокупность (псевдовыборку) для построения регрессии с бинарной зависимой переменной?

Как оценить компетентность эксперта и адекватность построенной таким образом модели?

Каким образом проверить согласованность мнений опрашиваемой группы экспертов?

Как оценить надежность расчетных характеристик, получаемых с помощью регрессии субъективных суждений?

какую содержательную интерпретацию имеют оценки, полученные в результате моделирования экспертных предпочтений?

Можно ли, а если можно, то как использовать статистические методы для проверки различного рода гипотез выдвигаемых относительно оцениваемых параметров и объектов?

По сути, в этих вопросах нет ничего нового. Практически все они в той или иной степени присутствуют в задачах прямого экспертного оценивания, обеспечивая надежность получаемых результатов. Но расчет и анализ характеристик, а также соответствующие выводы на их основе в новом подходе отличаются от того, как это делается в традиционном, поэтому требуют специального рассмотрения.

3.1.2. Эконометрический подход к построению моделей субъективных предпочтений.Решение первого и, очевидно, самого главного вопроса, связанного с моделированием субъективных предпочтений, требует построения регрессионного уравнения специального вида. Проблема, которую необходимо преодолеть при реализации этого подхода, связана, прежде всего, с тем, что применение линейной регрессии

(3.2)

для рассматриваемого случая не может привести к успеху, так как значения линейной формы

,

принадлежат непрерывной количественной шкале, а переменная у, отражающая мнение эксперта, изменяется дискретно, принимая всего два значения. Поэтому для исследования статистической зависимости между бинарной переменной у и количественными данными Хрекомендуется строить специальные регрессионные модели.

В настоящее время разрабатываются два подхода, позволяющих строить такие модели. В первом предусматривается построение линейной вероятностной модели. а во втором – нелинейных, получивших название логит- и пробит-моделей. Нас будут интересовать нелинейные модели. С их помощью зависимость устанавливается не между переменной у и набором данных Х, а между вероятностью того, что i-е значение бинарной переменной равно 1 при условии 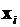, т.е. между , и линейной формой . Сразу заметим, что с помощью такого подхода моделирование экспертных предпочтений представляет собой более естественный процесс с хорошо понимаемой содержательной интерпретацией. Однако и в этом случае применение линейной формы вряд ли увенчается успехом, так как значение линейной функции может быть как отрицательным, так и превосходить единицу, что явно не согласуется с возможными значениями вероятности. Поэтому целесообразно для моделирования величин использовать функции, областью значений которых является отрезок [0, 1], а линейная форма играет роль аргумента в этих функциях, т.е. должна иметь место модель вида

. (3.3)

Чтобы запись модели в такой форме была корректной, функция должна удовлетворять следующим требованиям:

1)

2) ;

3) ;

4) .

В практике решения прикладных задач в качестве F, как правило, используются две функции. Если такой функцией является стандартная нормальная вероятностная функция распределения

, (3.4)

то регрессионная зависимость называется пробит-моделью. В случае, когда используется логистическая функция

(3.5)

зависимость называется логит-моделью.

Обе функции удовлетворяют всем четырем условиям, сформулированным выше, и, кроме того, являются симметричными относительно , т.е. и . Эти свойства значительно упрощают всевозможные преобразования тех выражений, в которых используются эти функции.

Таким образом, понимая под функцией регрессии зависимость «в среднем», между зависимой и независимыми переменными, можно записать

, (3.6)

где – одна из выше приведенных функций распределений.

Отражая тот факт, что реальная зависимость не всегда совпадает с математическим ожидание и, кроме того, ее значения могут отличаться даже на совпадающих наборах значений независимых переменных введем в рассмотрение случайную составляющую и окончательно запишем

, (3.7)

Нелинейный характер этих моделей, естественно, по сравнению с линейными моделями требует более сложный математический аппарат, который, к сожалению, не изложен на русском языке в форме, доступной для понимания. Поэтому ниже будет приведено достаточно подробное описание всего комплекса формальных процедур построения и анализа моделей, которые нами используются для прогнозирования субъективных предпочтений. Уровень детализации в изложении материала практически исключает в рассуждениях моменты, требующие самостоятельного восстановления преобразований, пропущенных якобы в силу их очевидности. Это позволит заинтересованным читателям в полном объеме освоить основы математического аппарата эконометрики качественных переменных. Полученные знания обеспечат грамотное восприятие и корректное практическое использование результатов моделирования.

Однако не следует эту возможность воспринимать как обязательный элемент знаний, без которого доступ к практическому применению этого аппарата существенно ограничен. Для тех, кто в большей степени ориентирован на практическое использование предлагаемых здесь методов, вполне достаточно уметь пользоваться одним из статистических пакетов, владеть приемами интерпретации результатов моделирования и освоить принципы формирования псевдовыборки, к изложению которых мы переходим.

3.1.3. Принципы формирования псевдовыборочных совокупностей. Вопрос применения для наших целей моделей бинарного выбора имеет как бы два аспекта. Один из них связан с методами построения этих моделей. Это тот аспект проблемы, основная направленность которого – корректное применение математического аппарата, как уже отмечалось, будет со всеми деталями рассмотрен ниже. Другой аспект представляет собой срез информационной составляющей, обнажающий проблему формирования специальных выборочных совокупностей и правомерность их использования в процедурах построения эконометрических моделей. Это как раз та проблема, на решение которой должны быть нацелены усилия экспертов.

Смысл основной задачи, стоящей перед экспертами, формирующими псевдовыборку, в том чтобы на данные выборочного множества перенести собственные представления о механизмах предполагаемых закономерностей между объясняющими переменными и ожидаемыми событиями. Тогда, если проведение такой процедуры было успешным, то по замыслу построенная модель должна отражать ту закономерность, руководствуясь которой эксперт оценивал степень воздействия выборочных значений на возможные проявления интересующего нас события. Таким образом, главное отличие псевдовыборки от выборки в том, что в ее данных содержится информация, которую эксперты сумели обнаружить и связать своими субъективными оценками со значениями зависимой переменной.

Способы формирования псевдовыборки зависят от смыслового содержания решаемой задачи. Это не совсем строго формализованные процедуры и поэтому для их успешного применения в каждом конкретном случае требуется адаптивное вмешательство. Рассмотрим типовые ситуации, которые возникают в практике анализа и прогнозирования бизнес процессов. Можно выделить три ситуации, которые отличаются принципами формирования псевдовыборки.

В первой ситуации псевдовыборку формируют непосредственно из выборочной совокупности с известными значениями зависимой (дихотомической) и независимыми переменными. Это тот случай, когда взаимосвязь между 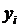и наборами 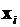( ) существует, но эксперты не уверены в абсолютной правомерности и надежности такой связи. Применяя принцип усиления взаимосвязей субъективными мнениями, они своими оценками уточняют возможность появления соответствующего значения 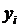при заданном наборе 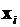. Уточняющие оценки удобно, хотя и не обязательно, получать в баллах, пользуясь для этого стобалльной шкалой. Таким образом, в результате опроса эксперта каждому наблюдению будет приписано определенное количество баллов. Причем, чем выше, по мнению эксперта, реальность наблюдаемого значения 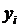при соответствующем наборе объясняющих переменных 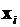, тем больше баллов приписывается данному наблюдению. Количество баллов удобно интерпретировать как частоту (число случаев), с которой данное наблюдение тиражируется в выборочной совокупности.

Вторая ситуация, которую мы намерены рассмотреть, предусматривает случаи, когда выборочное множество состоит только из объясняющих переменных и требуется на основе принципа субъективной идентификации взаимосвязей восстановить значения бинарной зависимой переменной. В соответствии с этим принципом эксперт каждому набору объясняющих переменных выборочной совокупности ставит в соответствие одно из возможных значений – 0 или 1 – зависимой переменной.

В сформированной таким образом псевдовыборке, как нетрудно понять, содержится информация, отражающая субъективное мнение по поводу того, какие условия, описываемые объясняющими переменными, благоприятны, а какие не благоприятны появлению некоторого события. Другими словами, экспертами сгенерированы значения бинарной переменной в зависимости от значений объясняющих переменных. Естественно, модель, построенная по данным так сформированной псевдовыборке, будет являться довольно грубым приближением к той зависимости, которую эксперты пытались описать своими предпочтениями в процессе формирования дискретной зависимой переменной. Поэтому желательно провести некоторые уточнения, используя для этого, например, описанный выше принцип усиления взаимосвязей субъективными мнениями.

Как следует из выше приведенных рассуждений, для получения надежных результатов в условиях второй ситуации целесообразно псевдовыборку формировать на основе двух сформулированных здесь принципов. Причем использование этих принципов может быть как последовательным, так и параллельным. Последовательное применение фактически уже было рассмотрено. Процедура параллельного использования принципов, по сути, приводит к тем же результатам. В ее рамках предполагается, что одновременно с идентификацией бинарного значения оценивается и возможная частота появления идентифицированного значения в выборочной совокупности. Для этих целей можно использовать не только балльное оценивание, как в случае первой ситуации, но и другие процедуры экспертного оценивания.

Особенность третьей ситуации в том, что исследуемые объекты имеют не только описание в виде набора показателей, но и имена. Например, это могут быть города, районы области, фирмы, товары и т.п. Предполагается, что эксперты знакомы с этими объектами до такой степени, что способны указать свои предпочтения относительно их использования в определенных целях. В принципе им могут быть известны и показатели, задающие формальное описание объектов. Но вне зависимости от уровня информированности экспертов, вне зависимости от полноты информационного описания этих объектов эксперты имеют субъективное представление об интегрированной ценности каждого объекта. Это как раз тот случай, когда для формирования псевдовыборки следует применять принцип субъективных предпочтений.

Если объектов не более двух-трех десятков, то принцип субъективных предпочтений удобно реализовать с помощью метода парных сравнений, подробное описание которого приводилось в предыдущей главе. Причем, сравнивать между собой следует объекты, а не их информационные описания. Это значительно упрощает работу экспертов, но только в том случае, если у них, действительно, имеются интегрированные представления об объектах.

Формирование значений бинарной переменной осуществляется по результатам экспертного опроса, отраженным в матрице парных сравнений. Объектам, которые получили больше половины предпочтений в процессе сравнения с другими объектами, приписывается 1, а получившим меньше половины – 0. Одновременно с формированием массива значений бинарной переменной можно, руководствуясь первым принципом, осуществить усиление предполагаемых связей. Для этого можно использовать или сумму очков, обеспечивших объекту предпочтение или сумму потерянных очков. Другими словами, если объекту приписана 1, то данные о нем в псевдовыборке повторяются столько раз, сколько он набрал очков при сравнении с другими объектами, а если – 0, то число повторений определяется числом потерянных очков.

Метод парных сравнений, являясь удобной процедурой формирования псевдовыборок, не всегда обеспечивает получение ожидаемого результата. Поэтому в арсенале исследователя должно быть несколько дополняющих друг друга процедур экспертного опроса, которые в случае необходимости могут комбинироваться при формировании одной и тоже псевдовыборочной совокупности.

Результатом применения выше описанных принципов является выборочная совокупность следующей структуры:

. . . . . . . . . . . .

.

где

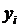– сгенерированное по результатам экспертного опроса значение бинарной переменной;

– набор показателей, которые, по мнению экспертов, определяют выбор сгенерированного ими значения бинарной переменной;

– определяемая экспертами частота повторяемости 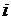– го наблюдения в выборочной совокупности.

Такая форма представления данных выборочной совокупности очень удобна для компьютерной обработки с помощью, например, пакета STATISTIСA.

Чтобы завершить обсуждение вопроса, связанного с формированием специальных выборочных совокупностей, необходимо провести обоснование правомерности использования для построения бинарных моделей данных, полученных подобным образом. Формально числовые данные пседовыборки ничем не отличаются от данных выборочной совокупности, полученных в результате статистических наблюдений. Более того, элементами псевдовыборки зачастую являются сами статистические наблюдения. И поэтому в силу того, что на формальном уровне данные этих якобы различных, по сути, выборочных совокупностей можно считать гомогенными, при построении модели не возникает вопросов вычислительного характера, но они сразу же возникают, как только появляется необходимость содержательной интерпретации и проверки статистической значимости результатов моделирования.

Правомерность проверки статистической значимости результатов моделирования по стандартным тестам, описание которых будет дано ниже, гарантируется свойствами случайной составляющей модели экспертного опроса (3.1). Если ошибки, которые допускает эксперт в своих предпочтениях при формировании псевдовыборки, независимы и нормально распределены, то случайная составляющая удовлетворяет необходимым условиям и применение тестов можно считать корректным. Подобные предположения не противоречат возможностям реальных ситуаций. Правда, здесь уместно заметить, что все, о чем мы говорим, имеет смысл только в том случае, когда эксперты относятся к своей работе добросовестно.

3.1.4. Оценка надежности и согласованности результатов моделирования экспертных предпочтений. Псевдовыборка, сформированная одним из вышеописанных способов, позволяет построить регрессионную модель, отражающую механизм субъективного выбора интересующих нас альтернатив. Этот механизм может отражать как индивидуальную точку зрения, так и групповое мнение, в зависимости от того, какая процедура использовалась при формировании выборки. Чтобы подобную модель использовать в практической деятельности, нужна уверенность в надежности получаемых с ее помощью результатов анализа и прогноза. Надежность, как нетрудно понять, при использовании подобного подхода может рождаться только из оценок свидетельствующих о компетентности экспертов и согласованности их мнений. Поэтому в центре дальнейших наших рассуждений будут именно эти вопросы.

Естественно, при оценке компетентности и согласованности можно использовать известные процедуры, применяемые в экспертных методах прямого оценивания. Их применение имеет смысл и позволяет получать некоторые гарантии надежности, но не в полном объеме. Необходимость в дополнительных характеристиках возникает потому, что при реализации рассматриваемого здесь подхода изменяется представление о содержательном смысле характеристик надежности. Прежде всего, это касается компетентности эксперта.

Переходя к рассмотрению компетентности, сразу согласимся с тем, что эксперт имеет право на собственное мнение, отличное от других экспертов. На наш взгляд, оригинальность в оценках не должна снижать компетентность, несмотря на то, что есть точка зрения [40], в соответствии с которой оценка компетентности тем выше, чем ближе индивидуальные оценки к групповым. Но с этой точкой зрения можно согласиться только при условии, что групповые оценки совпадают или почти совпадают с истинными. Вполне возможна ситуация, когда вопреки нашим ожиданиям групповые оценки далеки от истинных значений и заключение о компетентности, сделанное на основе близости индивидуальной оценки к такой групповой, теряет смысл.

Независимо от сделанного замечания и не взамен общепринятого подхода, введем в рассмотрение еще одну составляющую компетентности. Оценка этой составляющей основана на положении, смысл которого в том, что эксперт не может быть компетентным, если его оценки противоречивы. Возникает естественный вопрос, как оценить уровень противоречивости экспертных суждений.

Содержательный смысл решаемой здесь задачи позволяет предложить следующий подход. Сформированная экспертами псевдовыборка представляет собой данные, которые, по сути, сгенерированы в соответствии с представлением эксперта о взаимосвязи предпочтений бинарного выбора с факторным пространством. Если модель хорошо подгоняется к этому набору данных, т.е. имеет достаточно высокий индекс отношения правдоподобия (коэффициент Макфаддена, который далее будет рассмотрен более подробно), то следует признать, что суждения эксперта не противоречивы, ему действительно удалось сформировать модель собственных суждений, и поэтому он может быть отнесен к группе компетентных специалистов.

Для этих же целей можно использовать энтропийный коэффициент предсказывающих возможностей построенной модели. Этот коэффициент имеет следующий вид:

. (3.8)

Для случая, когда расчетные значения модели в точности совпадают с фактическими значениями дихотомической переменной, значение коэффициента равно нулю, т.е. во всех случаях модель обеспечивает безошибочный выбор, не оставляя место для сомнений в пользу альтернативы. Максимальный уровень энтропии ( ) получается в случае, когда для всех рассмотренных ситуаций . Во всех остальных случаях . Величина коэффициента показывает средний уровень неопределенности в каждом случае бинарного выбора, которая остается после построения модели.

Случай, когда построенная модель оказывается неадекватной, свидетельствует о некомпетентности эксперта, так как его взгляды на исследуемую проблему были противоречивы. Механизм, трансформирующий противоречивость взглядов в неадекватность модели можно представить следующей схемой рассуждений. Противоречивость является следствием неуверенности эксперта в собственных суждениях. В свою очередь, неуверенность нарушает логику, которой он должен придерживаться в процессе реализации своих предпочтений на выборочном множестве. В силу этого в сформированной псевдовыборке содержатся данные, слабо согласованные со значениями бинарной переменной. Несогласованность исключает возможность восстановления той зависимости, которой якобы пользовался эксперт, формируя псевдовыборку.

Таким образом, действительно, модель имеет плохую точность в тех случаях, когда псевдовыборка формировалась некомпетентным образом. Поэтому уровнем адекватности модели имеет смысл измерять компетентность эксперта. Чем выше уровень адекватности (коэффициент Макфаддена) или ниже остаточная энтропия (энтропийный коэффициент), тем компетентней действовал эксперт, распределяя свои предпочтения между наблюдениями выборочной совокупности.

Переходя к рассмотрению вопроса о согласованности оценок, сразу заметим, что, как и в случае прямого экспертного опроса, в рассматриваемом подходе действует тезис – доверие групповым оценкам выше, чем индивидуальным. Действие тезиса возможно только при согласованности индивидуальных оценок. Следовательно, не любая групповая оценка обладает высокой надежностью. На первый взгляд может показаться, что для проверки согласованности можно воспользоваться двумя подходами: в соответствии с первым проверять согласованность до построения модели, в соответствии со вторым – после построения по результатам моделирования.

От первого подхода сразу нужно отказаться, Дело в том, что псевдовыборка, сформированная с ориентиром на согласованное мнение экспертов, не всегда гарантирует построение адекватной модели. Это бывает в том случае, когда согласованными оказались мнения некомпетентных экспертов. Подобная ситуация не возникает в задачах прямого экспертного оценивания. В них компетентность оценивается либо экзогенно и тогда она не связана с результатами опроса, либо в зависимости от того, на сколько соответствующее индивидуальное мнение похоже на групповое.

Второй подход представляет собой авторское решение задачи, в рамках которой проверяется согласованность экспертных суждений. Как и в случае прямого экспертного оценивания в предлагаемом подходе предусматривается проверка согласованности мнений двух экспертов и проверка согласованности мнений всей группы экспертов, принявших участие в экспертизе. Обе проверки основаны на одной и той же идеи. Смысл этой идеи в том, что эксперты с близкими мнениями распределяют свои предпочтения по выборочной совокупности таким образом, что полученные псевдовыборки обеспечивают построение почти идентичных моделей. Таким образом, проверка согласованности сводится к статистической проверке значимости уровня идентичности. Выполнить такую проверку можно несколькими способами.

На наш взгляд, наиболее приемлемым следует считать способ, который позволяет не только оценить статистическую значимость, но и получить содержательно интерпретируемую величину, характеризующую уровень идентичности моделей и, следовательно, уровень согласованности экспертов. В качестве такой величины удобно использовать коэффициент Юла, который измеряет тесноту связи между двумя дихотомическими переменными.

Формально с помощью этого коэффициента мы можем оценить тесноту связи между предикторными возможностями двух моделей бинарного выбора. Для этого заполняется таблица сопряженности следующего вида:

Модель 1-го эксперта
Коды
	a	в
	c	d

Правило заполнения таблицы сопряженности довольно простое. В верхней левой клеточке стоит число случаев, когда предсказания по обеим моделям совпадали и были равны 1, в нижней правой – число случаев, когда обе модели предсказали 0. В остальных клеточках стоит число несовпадающих предсказаний. Коэффициент Юла рассчитывается по формуле

. (3.9)

При полном совпадении предсказанных значений и мы наблюдаем случай, когда мнения экспертов идентичны, при мнения экспертов противоположны, а при – независимы. Чем ближе значение коэффициента к 1, тем выше уровень согласованности экспертных мнений.

Для проверки групповой согласованности нет подходящего измерителя. Но можно предложить двухэтапную процедуру. На первом этапе для каждой пары экспертов вычисляется коэффициент сопряженности Юла, и все эксперты делятся на две группы. В первую группу включаются только те эксперты, предсказанные значения, по моделям которых имеют положительную связь между собой. Из коэффициентов сопряженности этой группы формируется матрица

.

Матрица обладает всеми свойствами необходимыми для того, чтобы с помощью обычной итерационной процедуры вычислить максимальное собственное значение , которое является действительным числом. Тогда в качестве меры, определяющей уровень согласованности экспертов, можно использовать величину

, (3.10)

в знаменателе которой стоит след матрицы без единицы.

Так определенный коэффициент согласованности будем называть характеристическим. Он равен 1, когда между всеми экспертами группы наблюдается абсолютное согласие, и равен 0, если результаты экспертного опроса статистически независимы.

С отбракованной на первом этапе группой экспертов поступают точно также.

Окончательно групповая оценка строится только для группы экспертов, имеющих согласованные мнения. Для этого все псевдовыборки объединяются в одну, по данным которой строится модель, отражающая групповое экспертное мнение. Ее и рекомендуется использовать в расчетах.

3.1.5. Предельный анализ моделей субъективных предпочтений. Предельный анализ факторов модели экспертных предпочтений проводится по схеме предельного анализа бинарной модели. Поэтому вначале рассмотрим все детали предельного анализа бинарной модели, а затем обсудим интерпретацию этих результатов для случая, когда моделируются экспертные предпочтения. Рассмотрение начнем с линейной модели.

Наши рекомендации