Развитие научных представлений об информации
Считается, что одним из первых понятие информации в научный оборот было введено Р.Фишером* в 1921 г. применительно к решению задач статистике. Статистика имеет дело с большим числом результатов наблюдений и заменяет обычно их полное перечисление указанием некоторых сводных характеристик. Иногда при такой замене происходит потеря информации, но при некоторых условиях сводные характеристики содержат всю информацию, содержащуюся в полных данных. Р.Фишером была предложена мера (среднего) количества информации, относительно неизвестного параметра, содержащейся в одном наблюдении. В круг интересов Р.Фишера входили и вопросы генетической теории эволюции, также непосредственно связанные с информацией [26,47].
Примерно в этот же период началось широкое распространение радиоэлектронных методов передачи сообщений на большие расстояния. Перед специалистами остро встала проблема качества и надежности связи.
Передаваемый сигнал это форма, в которую преобразованы сообщения. Очень важно как можно плотнее «наполнить» сигнал полезными данными, а при получении «извлечь» их с минимальными потерями, которые неизбежны при прохождении сигнала в физической среде. Для решения этой задачи требовалась разработка методов количественной оценки передаваемых сведений.
В результате многочисленных исследований в середине 30-40-х годов ХХ в. такие методы были созданы.
Основы теории информации, как самостоятельного научного направления были изложены в статье «Математическая теория связи» (1948 г.) выдающегося американского ученого и инженера К.Шеннона (1916-2001). Эта статья дала толчок интенсивному развитию математической теории передачи информации, углубленным исследованиям вопросов ее количественного измерения [47,46]. Методы данной теории позволили определять информационные характеристики конкретных видов сообщений (письменной и устной речи, фотографических и телевизионных изображений и пр.).
Цели, которые ставил перед собой Шеннон, были связаны с чисто техническими вопросами радиоэлектронной связи. Он решал проблемы повышения эффективности и надежности передачи данных. Однако в дальнейшем, благодаря своему общему характеру, работы Шеннона оказали большое влияние на все исследования, относящиеся к передаче и хранению какой бы то ни было информации в природе и технике. В дальнейшем идеи, как ее сегодня называют, классической теории информации стали использоваться в метрологии, нейрофизиологии, генетике, лингвистике и т.д.
Необходимо отметить, что работа Шеннона базировалась на трудах многих ученых, работающих в этой и смежных областях. Важную роль в становлении и развитии теории информации сыграли работы российских математиков и инженеров В.А.Котельникова (1908), А.Н.Колмогорова (1903-1987) , А.Я.Хинчина (1894-1959), А.М Яглома, А.А.Харкевича (1904-1965) и др. [21,46].
Котельников работал над совершенствованием методов радиоприема, разработкой методов борьбы с помехами. Теорема Котельникова, на которой построен принцип действия электронных машин, телевидения, систем связи, была сформулирована еще в 1933 г., до возникновения современной теории информации. Согласно этой теоремы максимальное число различных элементарных сигналов, которые можно передать по линии связи за единицу времени, является некоторой технической характеристикой линии, которую нельзя изменить, не внося изменений в саму линию. Данный вывод играет основную роль во всех применениях теории информации к вопросу о передаче непрерывных сигналов. Клод Шеннон, ссылался на его работу.
А.Н.Колмогоров считается одним из крупнейших математиков ХХ столетия. Он был одним из первых российских ученых, осознавших значение работ К.Шеннона по теории информации. Он обобщил и применил понятие энтропии в ряде областей математики, создав несколько новых научных математических направлений. В последние годы своей творческой деятельности он работал над созданием алгоритмических основ теории информации и теории вероятностей.
Исторически первые шаги к введению понятия энтропии как меры степени неопределенности сообщений были сделаны в 1928 г. американским инженером-связистом Р.Хартли, предложившим за отправную точку для информационной оценки события принимать его неопределенность и количественно характеризовать степень неопределенности события с n различными исходами числом log n.
До этого понятие энтропия широко использовалось в физике. Первым в 1865 г. его ввел немецкий ученый Р.Клаузиус (1822-88) для характеристики состояния термодинамических систем. Несколько позже оно стало использоваться в статистической физике как мера вероятности пребывания системы в данном состоянии. Австрийский физик Людвиг Больцман (1844-1906) в 1872 г. сформулировал принцип, устанавливающий соотношение между энтропией и ее термодинамической вероятностью через логарифмическую функцию и некую постоянную, в последствии названную в его честь [21,35].
Идея вероятностного подхода к оценке количества информации основывалась на следующих моментах. Существует множество примеров различных событий, характеризующихся одинаковой неопределенностью. Например, встреча на одном из 4-х углов перекрестка, выбор одной из 4-х карт различной масти и т.д. Во всех этих случаях имеет место неопределенность, характеризующаяся возможностью выбора одного из четырех вариантов.
Логично считать, что количество информации, полученной в результате совершения события, будет одинаковым независимо от сути процессов. Сообщения, которые могут быть получены при каждом из этих выборов, можно обозначить символами А, Б, В, Г и, не вдаваясь в конкретный смысл события, рассматривать его отвлеченно, просто как выбор некоторого элемента (символа) из четырех возможных. При этом логично считать, что количество полученной информации, не связанной с конкретным содержанием события, будет одинаковым при выборе одного из четырех символов во всех случаях.
Соответственно можно привести примеры событий, обладающих большей или меньшей неопределенностью, например, выпадение орла или решки при бросании монетки либо одной из шести сторон игральной кости.
Всю совокупность символов, которыми закодированы варианты возможных событий и сообщений о них, называют алфавитом сообщений. Зная алфавит сообщений, можно реализовать предложенный Р.Хартли структурный (или комбинаторный) подход к определению количества информации в сообщении.
Суть его состоит в том, чтобы оценивать неопределенность получения от источника того или иного сообщения исходя из общего множества возможных сообщений, величина которого в свою очередь обусловлена количеством информационных элементов, комбинаций этих элементов и связей между ними.
Более подробно содержание и особенности этого подхода мы рассмотрим ниже, а здесь упомянем еще несколько научных направлений, сыгравших важнейшую роль в становлении и широком распространении понятия информации.
Существует особая, очень тесная связь между теорий информации и другой важнейшей наукой, сформировавшейся в ХХ в., – кибернетикой.
В том же 1948 г., когда была опубликована знаменитая статья Шеннона, вышла в свет книга американского ученого Норберта Винера (1894-1964) «Кибернетика, или связь в животном и машине», в которой он обобщил общие принципы построения и работы любых управляющих систем, показал ключевую роль информации в управлении [6].
Основная идея книги – подобие процессов управления и связи в технических, биологических и социальных (организационных) системах. Эти процессы по своей природе прежде всего являются процессами передачи, хранения и переработки информации, т.е. различных сигналов, сообщений, сведений. Отсюда мысль о возможности создания общей для систем любого класса теории управления. Книга Винера стала итогом работы организованного им совместно с физиологом Артуром Розенблютом в годы Второй мировой войны семинара, в котором принимали участие математики, нейрофизиологи, специалисты по теории связи и вычислительной технике.
По словам Винера, их работа серьезно затруднялась отсутствием общей терминологии, даже хотя бы единого названия той области, которой они занимались. В ходе продолжительных обсуждений был сделан вывод, что вся существующая к тому времени терминология не может способствовать в надлежащей степени развитию этой области, и по примеру других ученых пришлось придумать искусственное неогреческое выражение для устранения пробела. Было решено назвать теорию управления и связи кибернетикой, от греческого «кормчий» – рулевой, ведущий судно. Этим хотели отметить, что судовые рулевые машины были действительно одними из самых первых хорошо разработанных устройств с обратной связью, лежащей в основе процессов управления.
Но позже выяснилось слово «кибернетика» не является неологизмом. Оно встречается довольно часто у Платона, где обозначает искусство управлять кораблем, искусство кормчего, а в переносном смысле, также искусство управлять людьми. В 1834 г. знаменитый французский физик А.Ампер (1775-1836), занимавшийся вопросами классификации наук назвал, по примеру древних, «кибернетикой» науку об управлении государством [6].
Кстати, по-видимому из-за того, что в становлении кибернетической науки принимали участие представители различных дисциплин, долгое время существовала путаница в определении предмета и соотношении кибернетики, теории информации и компьютерных наук.
Процессы управления действительно неразрывно связаны с процессами сбора, передачи и обработки информации, изучение которых является предметом теории информации. Но из этого не следует делать вывод, что эта теория является разделом кибернетики. Теория информации занимается изучением процессов преобразования информации более широко, часто вне связи с процессами управления.
Одной из главных задач теории информации является повышение помехоустойчивости передачи сообщений. Для этого разрабатываются специальные методы кодирования. Возникло даже новое большое направление – теория кодирования, которое некоторые специалисты считают самостоятельной научной дисциплиной. Другие же полагают, что к уже началу 70-х годов ХХ в. сама классическая теория информации свелась в первую очередь к теории кодирования.
А кибернетика – это наука об общих принципах управления в различных системах: технических, биологических, социальных и др. Кибернетика исследует любые управленческие процессы, причем независимо от того, используется ли для их реализации компьютерная техника или нет. Однако уже на самых ранних этапах развития этой науки стало понятно, многие технические системы достигли такого уровня сложности, который не позволяет управлять ими с требуемой быстротой и точностью без помощи автоматических или автоматизированных систем обработки информации. И поэтому вся история становления кибернетики теснейшим образом переплетается с развитием вычислительной техники.
Выдающийся американский ученый фон Нейман, разработавший принципиальную схему работы вычислительной машины, также считается одним из родоначальников кибернетики. Его работы во многом способствовали ее становлению. Но компьютеры могут использоваться для обработки любой, не обязательно управленческой информации, и поэтому отождествлять кибернетику с компьютерной обработкой информации также совершенно неправильно.
Примерно в это время, в 40-50 гг. ХХ в., параллельно с кибернетикой и теорией информации начала формироваться и еще одна наука, получившая в англоязычных странах название computer science (наука о компьютерной технике).
Считается, что чуть позже, в 60-х гг. во Франции для обозначения области, занимающейся автоматизированной обработкой информации с помощью электронных вычислительных машин, стали использовать термин «информатика» (Informatique), образованный объединением слов Information и Automatique (информация и автоматизация) [13,46].
В некоторых учебниках можно прочитать, что слово «информатика» появилось в русском языке в 70-х годах ХХ в. и позаимствовано из французского. На наш взгляд это случилось несколько позже. Широкое распространение этот термин получил в период массового внедрения персональных компьютеров в 80-х гг. Решение об организации нового отделения информатики, вычислительной техники и автоматизации в Академии наук СССР было принято в 1983 году. Вскоре были введены одноименные предметы в школьные и вузовские программы (кафедра информатики ГУУ начала работать в самом конце 80-х). Примерно в это же время абитуриенты начали сдавать вступительный экзамен по информатике.
По поводу появления термина «информатика» есть и другие точки зрения. Согласно одной из них научная дисциплина именно с таким названием существовала и успешно развивалась с 40-50 гг. Она исследовала структуру и общие свойства научной информации, т.е. сведений, отображающих объективные закономерности природы, общества и мышления, изучала процессы обмена научной информацией – от устного общения на конференциях до публикаций в виде научных статей или монографий. В практическом плане информатика вырабатывала способы сбора, хранения, поиска, распространения научной информации.
Есть также мнение, что информатика зародилась в рамках науки об обработке документов, основанной бельгийским ученым Полем Отле и была тесно связана с делопроизводством, библиотечным и архивным делом, книговедением и т.п. А пришедшее к нам из Франции слово не стало новым, просто его более широкое значение вытеснило старое [46].
Нет единства взглядов у ученых не только на историю формирования данного научного направления, но и на его предмет и место в современной системе наук.
Многие по-прежнему считают, что информатика является одним из направлений кибернетики и должна исследовать процессы передачи и обработки управленческой информации (не обязательно машинной). Другие полагают, что информатика – это область человеческой деятельности, связанная исключительно с процессами преобразования информации с помощью компьютеров.
Нам представляется более правильной вторая точка зрения. Информатика как фундаментальная наука должна заниматься разработкой методологии автоматизации информационных процессов в различных сферах деятельности, исследованием и обобщением знаний об автоматизированных информационных системах и технологиях, выявлением общих закономерностей их создания и функционирования.
Изучением же информационных процессов в более широком контексте следует заниматься в рамках отдельной дисциплины, которую, видимо правильно, называть «Информационные технологии», предметом которой должны стать любые информационные процессы вне зависимости от того, автоматизированы они или нет. Эта дисциплина должна интегрировать знания, накопленные в этой области другими науками: философией, кибернетикой, информатикой, языкознанием, лингвистикой, биологией, психологией и пр.
А теперь рассмотрим более подробно содержание основных научных подходов к понятиям информации и информационного процесса.
Информационная энтропия
Как уже отмечалось выше, в 20-х гг. прошлого века инженеры-связисты предложили за отправную точку для информационной оценки событий принимать их неопределенность и количественно характеризовать степень неопределенности события логарифмом от числа возможных исходов события.
Пусть имеется источник с n-равновероятными исходами сообщений. В этом случае можно говорить о том, что неопределенность одного исхода находится в некоторой функциональной зависимости от количества возможных исходов: H = f (n).
Каковы логические посылки для выбора данной функции?
1. С увеличением числа возможных исходов неопределенность должна возрастать.
2. При n = 1, когда возможен только один исход, опыт приобретает априорную определенность и его неопределенность должна обращаться в ноль.
3. Логично считать, что неопределенность сложного опыта, заключающегося в одновременном выполнении двух опытов в двух независимых друг от друга источниках, должна быть больше, чем неопределенность каждого из этих опытов, так как к неопределенности одного из них добавляется неопределенность другого. Желательно, чтобы неопределенности составляющих опытов суммировались. Т.е. функция Н должна обладать свойством аддитивности.
Можно показать, что одновременно этим условиям удовлетворяет только логарифмическая зависимость:
если n – число возможных сообщений, то неопределенность, приходящаяся на одно сообщение, определяется логарифмом общего числа возможных сообщений: H = log n;
если существуют два независимых источника, которые содержат n1 и n2 возможных сообщений, то общее число возможных сообщений n = n1 ´ n2, а неопределенность сложного опыта g, состоящего из двух независимых опытов a и b с количествами равновероятных исходов n1 и n2, измеряется величиной:
Н(g) = log (n1 ´ n2) = log n1 + log n2 = Н(a) + Н(b).
В приведенных выражениях для определения количества информации логарифмирование можно производить по любому основанию, однако наиболее удобно (и в настоящее время общепринято) использовать логарифмы по основанию два. В дальнейшем изложении данное условие не будет специально оговариваться, и везде будут использоваться логарифмы двоичные.
При n= 2 приходим к единице измерения неопределенности H = log2 2 = 1, получившей название двоичной единицы или бит (bit) «binary unit» или в компьютерной интерпретации – «binary digit» – двоичный разряд. Иными словами, двоичная единица – есть единица измерения степени неопределенности, представляющая неопределенность, которая содержится в одном опыте, имеющем два равновероятных исхода.
Так как в двоичной системе счисления каждый разряд числа с равной вероятностью может принимать значения 0 или 1, то соответственно и количество информации, приходящееся на один двоичный разряд (двоичную цифру), оказывается равным 1 биту. При обработке информации в машинах, ради удобства представления слов в виде совокупности неделимых частей некоторой стандартной длины в качестве таких частей выбраны 8-разрядные порции. Поэтому наряду с битом получила распространение укрупненная единица – байт, равный 8 битам. Кроме того, для измерения больших объемов информации широко используются более укрупненные единицы количества информации: килобит (К бит) и килобайт (К байт), а также мегабит (М бит) и мегабайт (М байт). Причем приставка «кило» условно обозначает не 1 тыс., а 210 = 1024 бит (байт), а «мега» — не 1 млн., а 220 = 1 048 576 бит (байт). Емкости памяти современных компьютеров уже измеряются гига- и терабайтами.
Недостаток структурного метода определения количества информации заключается в том, что при его использовании никак не учитывается различная вероятность поступления сообщений от источника. Между тем очевидно, что этот фактор должен влиять на количество полученной информации.
В перечисленных примерах вероятность поступления того или иного сообщения одинакова. Но на практике подавляющее число источников характеризуется разной вероятностью происходящих в них событий и, следовательно, не одинаковой вероятностью появления сообщений об этих событиях.
Рассмотрим пример: в нашем распоряжении есть две коробки, в каждой из которых имеется по 1000 шариков. Будем считать событием извлечение шарика из коробки. Совершение события снимает его неопределенность.
Пусть в одной коробке находится 999 черных и 1 белый шар; а в другой по 500 черных и белых. В этом случае сообщение об извлечении черного шара из первой коробки практически не несет информации, т.е. количество информации приближается к нулю. Во втором же случае, когда предсказать, какого цвета шарик будет извлечен, гораздо сложнее, сообщение о свершенном событии несет значительно больше информации.
Т.е. существует объективная необходимость в численной оценке степени неопределенности процессов с разной вероятностью исходов и разработке соответствующего математического аппарата.
Получаемая информация приводит к снятию некоторой априорной (имеющейся до опыта) неопределенности. Поэтому можно считать, что в первом случае, источник сообщений был для получателя почти полностью определенным, так как он, даже не осуществляя опыта, знал, что извлечет черный шар. Сообщение об извлечении черного шара несет в себе количество информации, близкое к нулю. А так как вероятность таких сообщений близка к единице, то и среднее количество информации на одно сообщение будет весьма мало. Во втором же случае, когда предсказать исход опыта невозможно, сообщение о событии несет значительно большее количество информации для получателя. Данные соображения указывают на необходимость учитывать при определении количества информации не только количество разнообразных сообщений, которые можно получить от источника, но и вероятность получения тех или иных сообщений (т.е. вероятностные характеристики источника). Именно они положены в основу статистического подхода к определению количества информации, предложенного К. Шенноном в 1948 г. и получившего самое широкое распространение при определении среднего количества информации, которое содержится в сообщениях от источников самой различной природы.
По Шеннону мера количества информации базируется на понятии информационной энтропии события и оценивает статистическую структуру сообщения, отвлекаясь от его содержания и полезности информации. Каждое событие характеризуется неопределенностью, зависящей от конечного числа возможных исходов и вероятности каждого из них.
Приведенное выше выражение H = log n можно записать в виде:
H = n ´ 1/n ´ log n = n ´ (-1/n ´ log 1/n),
где 1/n = P – вероятность любого из n равновероятных исходов опыта; т.е.
H = n ´ (-P ´ log P).
Пусть опыт a характеризуется таблицей вероятностей (табл.1).
Таблица 1
Вероятности исходов опытаa
| Исходы опыта | А1 | А2 | … | Ai | … | An |
| Вероятности исходов | PA1 | PA2 | … | PAi | … | PAn |
Тогда меру неопределенности такого опыта можно записать:
Н(a) = - PA1 ´ log P A2 - P A2 ´ log P A1 - ... - P An ´ log P An
или
n
Н(a) = - S (PAi ´ log P Ai ).
i = 1
Эту величину называют энтропией опыта a. Энтропия – это мера степени неопределенности, одно из базовых понятий классической теории информации.
Анализ данного выражения позволяет сделать следующие выводы:
· любое слагаемое в этой формуле всегда положительно, так как для любого исхода всегда справедливо неравенство: 0 £ PAi £ 1, следовательно, log PAi всегда отрицателен и, таким образом, энтропия любого события всегда положительна, т. е. Н ³ 0;
· может быть строго математически доказано, что энтропия опыта равна нулю лишь в том случае, когда одна из вероятностей PAi равна единице, а все остальные равны нулю, т.е. когда исход опыта не содержит никакой неопределенности;
· наибольшей неопределенностью среди всех опытов, имеющих n исходов, характеризуется опыт, у которого все исходы равновероятны. Энтропия опыта с равновероятными исходами будет максимальной.
Данные выводы могут быть проиллюстрированы на примере зависимости энтропии опыта с двумя возможными исходами (n = 2) как функции вероятности одного из исходов P. В этом случае вероятность другого исхода будет тогда равна (1 - P), а соответствующее выражение для энтропии будет иметь вид:
H(p) = - p ´ log p - (1 - p) ´ log (1 - p).
На рис. 1. приведен график этой Н(р) для значений р в пределах от 0 до 1. Из графика видно, что при вероятности одного из исходов, равной 0 (и, следовательно, вероятности другого исхода, равной 1), и при вероятности первого исхода, равной 1 (и вероятности второго исхода, равной 0), энтропия Н опыта обращается в нуль, а при равной вероятности обоих исходов (р = 0,5) энтропия опыта достигает максимальной величины, т. е. равна 1.
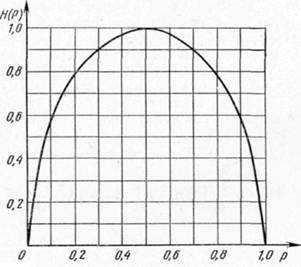
Рис. 1. График зависимости Н(р) опыта с двумя возможными исходами от вероятности одного из исходов р
