Глава 2. понятие информации и методы ее измерения

ГЛАВА 2. ПОНЯТИЕ ИНФОРМАЦИИ И МЕТОДЫ ЕЕ ИЗМЕРЕНИЯ

Информационная энтропия

Как уже отмечалось выше, в 20-х гг. прошлого века инженеры-связисты предложили за отправную точку для информационной оценки событий принимать их неопределенность и количественно характеризовать степень неопределенности события логарифмом от числа возможных исходов события.

Пусть имеется источник с n-равновероятными исходами сообщений. В этом случае можно говорить о том, что неопределенность одного исхода находится в некоторой функциональной зависимости от количества возможных исходов: H = f (n).

Каковы логические посылки для выбора данной функции?

1. С увеличением числа возможных исходов неопределенность должна возрастать.

2. При n = 1, когда возможен только один исход, опыт приобретает априорную определенность и его неопределенность должна обращаться в ноль.

3. Логично считать, что неопределенность сложного опыта, заключающегося в одновременном выполнении двух опытов в двух независимых друг от друга источниках, должна быть больше, чем неопределенность каждого из этих опытов, так как к неопределенности одного из них добавляется неопределенность другого. Желательно, чтобы неопределенности составляющих опытов суммировались. Т.е. функция Н должна обладать свойством аддитивности.

Можно показать, что одновременно этим условиям удовлетворяет только логарифмическая зависимость:

если n – число возможных сообщений, то неопределенность, приходящаяся на одно сообщение, определяется логарифмом общего числа возможных сообщений: H = log n;

если существуют два независимых источника, которые содержат n₁ и n₂ возможных сообщений, то общее число возможных сообщений n = n₁ ´ n₂, а неопределенность сложного опыта g, состоящего из двух независимых опытов a и b с количествами равновероятных исходов n₁ и n₂, измеряется величиной:

Н(g) = log (n₁ ´ n₂) = log n₁ + log n₂ = Н(a) + Н(b).

В приведенных выражениях для определения количества информации логарифмирование можно производить по любому основанию, однако наиболее удобно (и в настоящее время общепринято) использовать логарифмы по основанию два. В дальнейшем изложении данное условие не будет специально оговариваться, и везде будут использоваться логарифмы двоичные.

При n= 2 приходим к единице измерения неопределенности H = log₂ 2 = 1, получившей название двоичной единицы или бит (bit) «binary unit» или в компьютерной интерпретации – «binary digit» – двоичный разряд. Иными словами, двоичная единица – есть единица измерения степени неопределенности, представляющая неопределенность, которая содержится в одном опыте, имеющем два равновероятных исхода.

Так как в двоичной системе счисления каждый разряд числа с равной вероятностью может принимать значения 0 или 1, то соответственно и количество информации, приходящееся на один двоичный разряд (двоичную цифру), оказывается равным 1 биту. При обработке информации в машинах, ради удобства представления слов в виде совокупности неделимых частей некоторой стандартной длины в качестве таких частей выбраны 8-разрядные порции. Поэтому наряду с битом получила распространение укрупненная единица – байт, равный 8 битам. Кроме того, для измерения больших объемов информации широко используются более укрупненные единицы количества информации: килобит (К бит) и килобайт (К байт), а также мегабит (М бит) и мегабайт (М байт). Причем приставка «кило» условно обозначает не 1 тыс., а 210 = 1024 бит (байт), а «мега» — не 1 млн., а 220 = 1 048 576 бит (байт). Емкости памяти современных компьютеров уже измеряются гига- и терабайтами.

Недостаток структурного метода определения количества информации заключается в том, что при его использовании никак не учитывается различная вероятность поступления сообщений от источника. Между тем очевидно, что этот фактор должен влиять на количество полученной информации.

В перечисленных примерах вероятность поступления того или иного сообщения одинакова. Но на практике подавляющее число источников характеризуется разной вероятностью происходящих в них событий и, следовательно, не одинаковой вероятностью появления сообщений об этих событиях.

Рассмотрим пример: в нашем распоряжении есть две коробки, в каждой из которых имеется по 1000 шариков. Будем считать событием извлечение шарика из коробки. Совершение события снимает его неопределенность.

Пусть в одной коробке находится 999 черных и 1 белый шар; а в другой по 500 черных и белых. В этом случае сообщение об извлечении черного шара из первой коробки практически не несет информации, т.е. количество информации приближается к нулю. Во втором же случае, когда предсказать, какого цвета шарик будет извлечен, гораздо сложнее, сообщение о свершенном событии несет значительно больше информации.

Т.е. существует объективная необходимость в численной оценке степени неопределенности процессов с разной вероятностью исходов и разработке соответствующего математического аппарата.

Получаемая информация приводит к снятию некоторой априорной (имеющейся до опыта) неопределенности. Поэтому можно считать, что в первом случае, источник сообщений был для получателя почти полностью определенным, так как он, даже не осуществляя опыта, знал, что извлечет черный шар. Сообщение об извлечении черного шара несет в себе количество информации, близкое к нулю. А так как вероятность таких сообщений близка к единице, то и среднее количество информации на одно сообщение будет весьма мало. Во втором же случае, когда предсказать исход опыта невозможно, сообщение о событии несет значительно большее количество информации для получателя. Данные соображения указывают на необходимость учитывать при определении количества информации не только количество разнообразных сообщений, которые можно получить от источника, но и вероятность получения тех или иных сообщений (т.е. вероятностные характеристики источника). Именно они положены в основу статистического подхода к определению количества информации, предложенного К. Шенноном в 1948 г. и получившего самое широкое распространение при определении среднего количества информации, которое содержится в сообщениях от источников самой различной природы.

По Шеннону мера количества информации базируется на понятии информационной энтропии события и оценивает статистическую структуру сообщения, отвлекаясь от его содержания и полезности информации. Каждое событие характеризуется неопределенностью, зависящей от конечного числа возможных исходов и вероятности каждого из них.

Приведенное выше выражение H = log n можно записать в виде:

H = n ´ 1/n ´ log n = n ´ (-1/n ´ log 1/n),

где 1/n = P – вероятность любого из n равновероятных исходов опыта; т.е.

H = n ´ (-P ´ log P).

Пусть опыт a характеризуется таблицей вероятностей (табл.1).

Таблица 1

Вероятности исходов опытаa

Исходы опыта	А1	А2	…	Ai	…	An
Вероятности исходов	PA1	PA2	…	PAi	…	PAn

Тогда меру неопределенности такого опыта можно записать:

Н(a) = - P_A1 ´ log P _A2 - P _A2 ´ log P _A1 - ... - P _An ´ log P _An

или

_n

Н(a) = - S (P_Ai ´ log P _Ai ).

^{i = 1}

Эту величину называют энтропией опыта a. Энтропия – это мера степени неопределенности, одно из базовых понятий классической теории информации.

Анализ данного выражения позволяет сделать следующие выводы:

· любое слагаемое в этой формуле всегда положительно, так как для любого исхода всегда справедливо неравенство: 0 £ P_Ai £ 1, следовательно, log P_Ai всегда отрицателен и, таким образом, энтропия любого события всегда положительна, т. е. Н ³ 0;

· может быть строго математически доказано, что энтропия опыта равна нулю лишь в том случае, когда одна из вероятностей P_Ai равна единице, а все остальные равны нулю, т.е. когда исход опыта не содержит никакой неопределенности;

· наибольшей неопределенностью среди всех опытов, имеющих n исходов, характеризуется опыт, у которого все исходы равновероятны. Энтропия опыта с равновероятными исходами будет максимальной.

Данные выводы могут быть проиллюстрированы на примере зависимости энтропии опыта с двумя возможными исходами (n = 2) как функции вероятности одного из исходов P. В этом случае вероятность другого исхода будет тогда равна (1 - P), а соответствующее выражение для энтропии будет иметь вид:

H(p) = - p ´ log p - (1 - p) ´ log (1 - p).

На рис. 1. приведен график этой Н(р) для значений р в пределах от 0 до 1. Из графика видно, что при вероятности одного из исходов, равной 0 (и, следовательно, вероятности другого исхода, равной 1), и при вероятности первого исхода, равной 1 (и вероятности второго исхода, равной 0), энтропия Н опыта обращается в нуль, а при равной вероятности обоих исходов (р = 0,5) энтропия опыта достигает максимальной величины, т. е. равна 1.

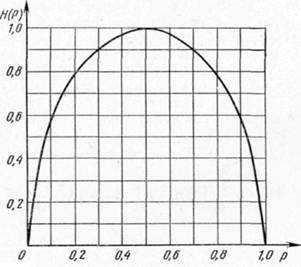
Рис. 1. График зависимости Н(р) опыта с двумя возможными исходами от вероятности одного из исходов р

Экономическая информация

Одной из важнейших разновидностей информации является информация экономическая. Она отражает процессы производства, распределения, обмена и потребления материальных благ и услуг. Ее отличительная черта – связь с процессами управления коллективами людьми и организациями.

Экономическая информация представляет совокупность данных, отражающих хозяйственные процессы и взаимосвязи между органами управления экономикой, а также соответствующие им процессы управления.

Следует отметить, что сегодня использование термина экономической информации не вполне оправдано. Существуют и организации, не ведущие экономическую (коммерческую) деятельность, но требующие реализации процессов управления. Поэтому более правильно использовать термин «организационная информация», т.е. информация, циркулирующая в системах организационного управления. Однако исторически сложилось так, что данный вид информации чаще называют экономической, производственно-экономической, социально-экономической, организационно-экономической и т.д.

Основным носителем информации в системах организационного управления является документ. Традиционно документ определяют как материальный носитель информации, используемый в системе управления и имеющий юридическую силу.

Для многих приложений менеджмента, экономики и права такая трактовка данного понятия является вполне оправданной. Однако при исследовании информационных процессов в организационных системах она является не совсем корректной. Дело в том, что при реализации управленческих функций руководители и специалисты вынуждены формировать и использовать множество «бумаг» , которые не являются юридическими документами, но все равно объективно необходимы для работы, а содержащиеся в них данные должны учитываться при анализе информационных процессов, например, в целях автоматизации. Поэтому мы будем в дальнейшем понимать под документом любой материальный носитель информации, используемый при решении задач организации.

Содержание значительной части управленческих документов раскрывается через понятия реквизит или показатель.

Реквизит – информационный параметр, описывающий определенное свойство объекта, процесса, явления и т.п. Например, данные о каждом сотруднике организации в отделе кадров представлены посредством одинаковых наборов реквизитов: фамилия, имя, отчество; пол; год рождения; место рождения; адрес проживания и т.д. Перечисленные реквизиты характеризуют свойства объекта «сотрудник».

Реквизит имеет наименование и значения. Значение реквизита может быть представлено либо числовыми данными, например, вес, зарплата, год приема на работу, либо качественными признаками, например, цвет волос, марка машины, фамилия. Реквизиты, имеющие численные, измеряемые значения, в литературе часто называют показателями. Т.е. показатель – это количественная характеристика какого-либо объекта, явления, процесса.

Термин показатель больше относится к содержательной характеристике объекта, он чаще используется специалистами в устной речи. Термин реквизит уже ближе к форме документирования данных на материальном носителе.

Такая ситуация сложилась и из-за того, что в документоведении под реквизитом понимают обязательные данные, которые в соответствие с инструкциями должен содержать правильно составленный и оформленный документ (например, наименование документа, дата выдачи, подписи).

Экономические показатели можно разделить на связанные (зависимые) и несвязанные (независимые). Взаимозависимость показателей может быть обусловлена содержательной связью их наименований, а также функциональной зависимостью между их значениями. В ряде случаев в сложных системах имеет место взаимосвязь нескольких показателей. Максимальный учет взаимосвязей показателей служит одним из важнейших факторов успешного решения ряда многих управленческих задач.

Многие управленческие документы имеют форму таблиц показателей. Поэтому в ряде случаев количество экономической информации целесообразно оценивать числом символов или строк документа, числом стандартных документов и показателей.

Однако другая, еще одна существенная часть управленческой документации представлена в форме обычных текстовых документов (письма, отчеты и пр.). Для них подобные количественные оценки в большинстве случаев лишены смысла. Поэтому для характеристики информационных процессов в организационных системах чаще приходится пользоваться качественными параметрами. Перечислим наиболее часто употребляемые параметры информации, используемой в сфере организационного управления:

· адекватность (точность) информации – характеризует уровень соответствия создаваемого с помощью полученной информации образа реальному объекту, процессу, явлению и т.п.;

· актуальность информации – характеризует степень сохранения ценности информации в момент ее использования;

· достаточность (полнота) информации – характеризует ее минимальный объем, достаточный для принятия правильного решения;

· достоверность информации – характеризует свойство отображения реальных объектов с необходимой точностью. Она может быть оценена вероятностью того, что значение отображаемого параметра отличается от истинного значения этого параметра в пределах необходимой точности. Достоверность также характеризует соответствие принятого сообщения переданному;

· доступность информации – характеризует уровень сложности процессов ее получения и восприятия конечным пользователем. Она обеспечивается разработкой и выполнением соответствующих процедур ее получения и преобразования. Семантическая форма информации должна быть согласована с тезаурусом пользователя;

· избыточность – характеризует степень превышение имеющегося объема информации по отношению к уровню, необходимому для принятия решения. Определенная информационная избыточность часто бывает полезной, так как повышает надежность функционирования систем управления. Но у избыточности есть и серьезные отрицательные стороны. Она вызывает необходимость усложнения организационных структур, увеличение финансовых и временных затрат на обработку информации и пр.;

· релевантность – характеризует степень соответствия исходной информации содержанию решаемой задачи или степень близости смыслового содержания документа, найденного в результате поиска содержанию запроса;

· репрезентативность информации – характеризует правильность и обоснованность отбора существенных признаков и связей отображаемого явления для адекватного отражения свойств объекта. Репрезентативность – это представительность информации, достаточная для обоснования решения, ради которого она собрана;

· своевременность информации – характеризует время ее поступления к пользователю, которое должно быть не позже заранее назначенного момента, согласованного с временем решения поставленной задачи. Запаздывание информации часто снижает, а иногда и сводит к нулю ее полезность;

· содержательность информации – отражает семантическую (смысловую) емкость, равную отношению количества семантической информации в сообщении к объему обрабатываемых данных;

· экономичность информации – характеризует уровень затрат на ее сбор, формирование, передачу и обработку [13,21].

Существуют и другие, качественные параметры информации. Ведутся поиски их рациональной количественной оценки. Но пока в этой области больше вопросов, чем ответов.

Кодирование

Кодирование можно определить как процесс представления информации в виде некоторых символов или их последовательностей (кодовых комбинаций).

Представление информации в виде слов-символов, формируемых в мозгу человека в процессе восприятия явлений окружающего мира, можно рассматривать в качестве примера естественного кодирования. В дальнейшем для фиксации этой информации на бумаге необходимо ее перекодирование в виде букв и их сочетаний, а для передачи по электрическому каналу связи — в виде электрических сигналов и т. д.

Все эти многочисленные этапы преобразования форм представления информации удобно называть, просто кодированием, опуская приставку «пере». В случае обратного перекодирования, принято употреблять термин декодирование.

Согласно строгой математической терминологии кодированием называется отображение какого-либо произвольного множества в множество конечных последовательностей (слов) в некотором алфавите, а декодированием — обратное отображение.

Это отображающее множество, включающее в себя множество знаков (символов) и слов (кодовых комбинаций), составленных из этих знаков по определенным правилам и предназначенных для однозначного отображения элементов отображаемого множества, называется кодом.

Конечное множество (список) попарно различных знаков, букв, цифр или любых других символов, применяемых в той или иной области (языке), носит название алфавита. Соответственно, рассматривая проблемы кодирования, можно говорить об алфавите соответствующего кода. Количество различных букв, входящих в алфавит, называют объемом алфавита.

Совокупность правил кодового обозначения объектов называют системой кодирования. К любой системе кодирования предъявляются следующие основные требования:

а) взаимная однозначность преобразований отображаемого множества в отображающее множество при кодировании и обратного преобразования при декодировании, что составляет необходимое условие отсутствия ошибок в интерпретации исходной информации;

б) экономичность кодирования, обеспечиваемая, прежде всего, минимизацией средней длины кодовой комбинации, а значит и длины информационных текстов, что в свою очередь обеспечивает снижение времени, необходимого для передачи и обработки информации, и экономию носителей информации;

в) помехоустойчивость, т.е. возможность обнаружения и исправления ошибок в кодовых комбинациях под влиянием тех или иных помех и сбоев в процессе передачи и обработки информации, повышающая достоверность работы кибернетических систем.

Необходимо отметить, что второе и третье требования взаимно противоречат друг другу, так как повышение помехоустойчивости кодов достигается увеличением длины кодовых комбинаций и, следовательно, снижает экономичность систем кодирования.

В технике связи и обработки информации предложено большое количество различных способов кодирования, обеспечивающих более или менее успешный компромисс в выполнении этих требований в различных кибернетических системах и условиях их функционирования.

При организации передачи и электронной обработки информации важным является выбор системы счисления, т.е. цифрового алфавита, в котором производится кодирование величин. При этом на практике наиболее удобной оказывается двоичная система счисления, при которой алфавит содержит лишь два значения: 0 и 1. При кодировании информации в двоичной системе счисления достигается наибольшая простота и надежность технических электронных устройств.

Кроме того, кодовые комбинации в двоичной системе счисления удобно представлять в виде импульсов тока или напряжения, приписывая значение «1» наличию импульса, а значение «0» — отсутствию импульса или импульсу противоположного знака. Преимущество двоичной системы счисления состоит также в чрезвычайной простоте арифметических операций над числами.

В силу этого подавляющее число цифровых вычислительных систем, как и прочих технических информационных устройств, работает с дискретной информацией, закодированной в двоичной системе счисления.

Кодирование экономической информации имеет свою специфику. В этой области в ходе многолетней работы по автоматизации процессов организационного управления выработаны свои особые системы кодирования, обеспечивающие удобную и эффективную обработки данных.

Наиболее распространенная система кодирования экономической информации основана на иерархической классификации объектов и формировании так называемых «классификаторов», представляющих собой упорядоченные по иерархическому принципу множества объектов, каждому из которых присвоен определенный код.

Код характеризуется длиной (число позиций в коде) и структурой (порядком расположения в коде символов, используемых для обозначения классификационного признака).

При иерархической системе классификации структура кода отображает иерархические связи классификационных признаков. Например, код студента университета содержит информацию о факультете, специальности, порядковом номере группы. Иерархическая классификация целесообразна, если необходимо агрегирование информации.

Существует и так называемая фасетная классификация, когда элементы структуры кода не зависят друг от друга. Например, код продукции предприятия, выпускающего керамическую плитку, может содержать информацию о ее размере, цвете, типе рисунка и т.д.

В нашей стране разработаны и применяются множество государственных, отраслевых, региональных классификаторов (отраслей промышленности, оборудования, профессий, единиц измерения и т.д.).

При проведении работ по автоматизации информационных процессов в организации создается множество локальных, специализированных классификаторов объектов этой организации (структурных подразделений, должностей, выпускаемой продукции и т.д.).

При создании локальных классификаторов небольшого объема часто удобно пользоваться порядковой системой кодирования предусматривающей последовательную нумерацию объектов числами натурального ряда. Можно использовать и смешанную серийно-порядковую систему кодирования, предусматривающую предварительное выделение групп объектов, которые составляют серию, а порядковая нумерация производится внутри каждой серии независимо.

ГЛАВА 2. ПОНЯТИЕ ИНФОРМАЦИИ И МЕТОДЫ ЕЕ ИЗМЕРЕНИЯ