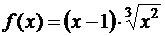Определение производной. Ее физическая и геометрическая интерпретация
ГЛАВА 3
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ЧИСЛОВЫХ ФУНКЦИЙ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
Основной предмет дифференциального исчисления составляет вычисление производной, изучение и использование ее свойств.
§1. ПРОИЗВОДНАЯ ЧИСЛОВОЙ ФУНКЦИИ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
Так что
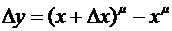 ,
,
и
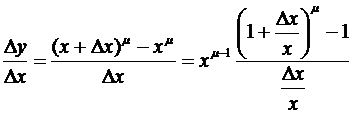 ,
,
где 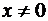 . Если воспользоваться пределом (1.21), то получим
. Если воспользоваться пределом (1.21), то получим
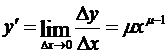 .
.
В частности,
1) если 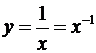 , то
, то 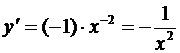 ,
,
2) если 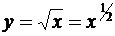 , то
, то 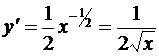 .
.
3. Показательная функция: 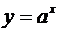 (а > 0 и а
(а > 0 и а 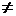 1, – ∞ < x < +∞). Здесь
1, – ∞ < x < +∞). Здесь
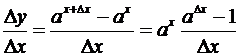 .
.
Воспользовавшись пределом, указанным в гл.1, §6, п.6.4, найдем:
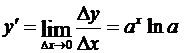 .
.
В частности, если 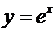 , то и
, то и 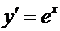 .
.
4. Логарифмическая функция: у = loga x (0 < a ¹1,0 < x <+¥). В этом случае
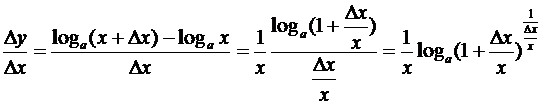 .
.
Учитывая, что 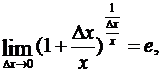 получим
получим 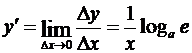 . В частности, если у = ln x, то
. В частности, если у = ln x, то 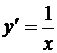 .
. 
5. Тригонометрические функции. Пусть у =sin x, тогда
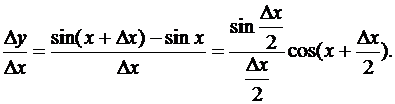
Пользуясь непрерывностью функции sin x и известным пределом 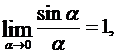 получим
получим
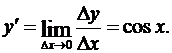
Аналогично найдем:
если у = cos x, то 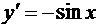 .
.
В случае 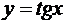 имеем
имеем
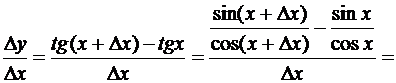
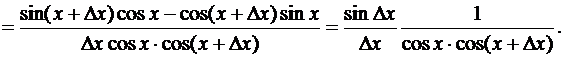
Отсюда, как и выше,
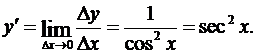
Аналогично,
если 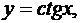 то
то 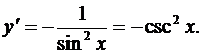
Теорема о непрерывности функции, имеющей производную
Теорема. Если функция 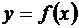 в некоторой точке x = x0 имеет (конечную) производную
в некоторой точке x = x0 имеет (конечную) производную 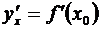 , то
, то
1) приращение функции может быть представлено в виде
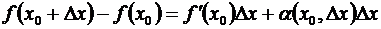 , (3.6)
, (3.6)
или, короче, 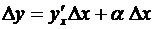 , где a есть величина, зависящая от Dx и вместе с ним стремящаяся к нулю, т.е.
, где a есть величина, зависящая от Dx и вместе с ним стремящаяся к нулю, т.е. 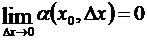 ;
;
2) функция в этой точке необходимо непрерывна.
Доказательство. 1) Согласно определению производной, 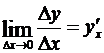 . Пользуясь теоремой, о представлении функции имеющей предел в виде суммы этого предела и бесконечно малой, запишем
. Пользуясь теоремой, о представлении функции имеющей предел в виде суммы этого предела и бесконечно малой, запишем
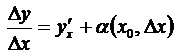 , где
, где 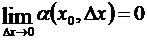 .
.
Определяя отсюда Dy, придем к формуле (3.6).
2) Чтобы доказать непрерывность функции, рассмотрим выражение (3.6). При Dx ®0 сумма в правой части (3.6) обращается в нуль. Следовательно, 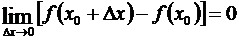 , или
, или 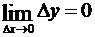 , а это означает, что функция в точке x0 непрерывна.
, а это означает, что функция в точке x0 непрерывна.
Из доказанной теоремы следует, что функция, имеющая производную в данной точке, будет непрерывной в этой точке. Однако непрерывная в данной точке функция не всегда имеет производную в этой точке. Так, в точке x0 = 1 функция y = |x – 1| является непрерывной, но производной в этой точке не имеет. Это означает, что данное условие является лишь необходимым.
Производная сложной функции
Теорема. Пусть 1) функция v = j(x) имеет в некоторой точке x производную 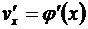 , 2) функция y = f(v) имеет в соответствующей точке v производную
, 2) функция y = f(v) имеет в соответствующей точке v производную 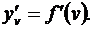 Тогда сложная функция у = f(j(x)) в упомянутой точке х также будет иметь производную, равную произведению производных функций f(v) и j(x): [ f(j (x)) ]' =
Тогда сложная функция у = f(j(x)) в упомянутой точке х также будет иметь производную, равную произведению производных функций f(v) и j(x): [ f(j (x)) ]' = 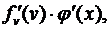 или короче
или короче
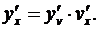 (3.7)
(3.7)
Доказательство.Придадим х произвольное приращение Δх; пусть Δv – соответствующее приращение функции v = j(x) и, наконец, Δу – приращение функции y = f(v), вызванное приращением Δv. Воспользуемся соотношением (3.6), которое, заменяя x на v, перепишем в виде 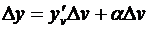 (a зависит от Δv и вместе с ним стремится к нулю). Разделив его почленно на Dx, получим
(a зависит от Δv и вместе с ним стремится к нулю). Разделив его почленно на Dx, получим
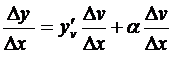 .
.
Если Dx устремить к нулю, то, согласно (3.6) (при условии, что у = v), будет стремиться к нулю и Δv, а тогда, как мы знаем, будет также стремиться к нулю зависящая от Δv величина a. Следовательно, существует предел
 ,
,
который и представляет собой искомую производную 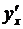 .
.
Таким образом, производная сложной функции равна произведению производной внешней функции на производную внутренней функции.
Случай сложной функции, полученной в результате нескольких суперпозиций, исчерпывается последовательным применением правила (3.7). Так, если у = f(u), u = j(v), v = y (x), то
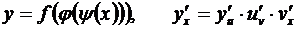 . (3.8)
. (3.8)
Примеры. 1. Пусть y = loga sin x,иначе говоря, y = loga v, где v = sin x. По правилу (3.7)
 .
.
2.  , т.е. y=eu, u = v2, v = sin x. По правилу (3.8)
, т.е. y=eu, u = v2, v = sin x. По правилу (3.8)
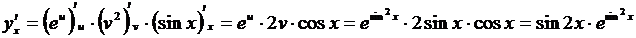 .
.
1.7. Производная показательно– степенной функции
Пусть u = u(x) > 0 и v = v(x) – функции, имеющие производные в фиксированной точке x. Найдем производную функции y = uv. Логарифмируя это равенство, получим: ln y = v ln u.
Продифференцируем обе части данного равенства по x:
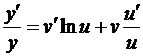 .
.
Отсюда 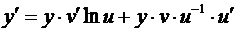 , или
, или
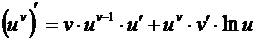 . (3.9)
. (3.9)
Таким образом, производная показательно – степенной функции состоит из двух слагаемых: первое слагаемое получается, если при дифференцировании предположить, что и есть функция от х, а v есть постоянная (т.е. рассматривать uv как степенную функцию); второе слагаемое получается, если предположить, что v есть функция от х, а u = const (т.е. рассматривать uv как показательную функцию).
Примеры.1. Если y = xtg x, то, полагая u = x, v = tg x,согласно (3.9) имеем
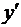 = tg x xtg x – 1 + xtg x ln x sec2x.
= tg x xtg x – 1 + xtg x ln x sec2x.
Прием, примененный в данном случае для нахождения производной и состоящий в том, что сначала находят производную логарифма рассматриваемой функции, широко применяется при дифференцировании функций: при отыскании производной функции эти функции сначала логарифмируют, а затем из равенства, полученного после дифференцирования логарифма функции, определяют производную функции. Такая операция называется логарифмическим дифференцированием.
2.Требуется найти производную от функции
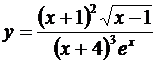 .
.
Логарифмируя, находим:
ln y = 2ln(x + 1) + 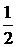 ln(x – 1) – 3 ln(x + 4) – x.
ln(x – 1) – 3 ln(x + 4) – x.
Дифференцируем обе части последнего равенства:
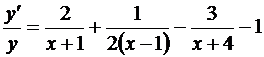 .
.
Умножая на у и подставляя  вместо у, получаем:
вместо у, получаем:
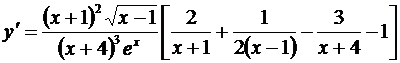 .
.
Бесконечные производные
Если 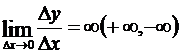 , то говорят, что функция в этой точке имеет бесконечную производную (и обозначают как обычно). Аналогично устанавливается понятие об односторонней бесконечной производной. Геометрически существование бесконечной производной означает, что касательная к кривой в данной точке перпендикулярна к оси абсцисс Ох (рис.16,б). В случаях (1) и (2) эта производная равна, соответственно +∞ и –∞ (обе односторонние производные совпадают по знаку); в случаях же (3) и (4) бесконечная производная не имеет определенного знака (односторонние производные разнятся знаками).
, то говорят, что функция в этой точке имеет бесконечную производную (и обозначают как обычно). Аналогично устанавливается понятие об односторонней бесконечной производной. Геометрически существование бесконечной производной означает, что касательная к кривой в данной точке перпендикулярна к оси абсцисс Ох (рис.16,б). В случаях (1) и (2) эта производная равна, соответственно +∞ и –∞ (обе односторонние производные совпадают по знаку); в случаях же (3) и (4) бесконечная производная не имеет определенного знака (односторонние производные разнятся знаками).
Пользуясь расширением понятия производной, можно дополнить формулу (3.4) о производной обратной функции указанием, что и в тех случаях, когда 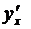 равна 0 или ∞, производная обратной функции
равна 0 или ∞, производная обратной функции 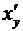 существует и равна, соответственно, ∞ или 0. Например, так как функция
существует и равна, соответственно, ∞ или 0. Например, так как функция 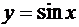 при х = ±p/2 имеет производную cos (±p/2) = 0, то для обратной функции х = arcsin у при у = ±1 существует бесконечная производная (именно,
при х = ±p/2 имеет производную cos (±p/2) = 0, то для обратной функции х = arcsin у при у = ±1 существует бесконечная производная (именно, 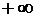 ).
).
Таблица основных формул для производных
Составим таблицу всех выведенных нами формул:
1. у = с = const, 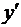 = 0;
= 0;
2. у = х, 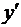 = 1;
= 1;
3. 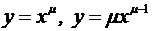 (
( 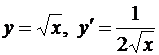 );
);
4. 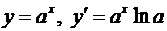 (
( 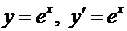 );
);
5. 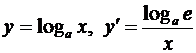 (
( 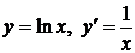 );
);
6. 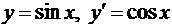 ;
;
7. y = cos x; 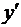 = – sin x;
= – sin x;
8. y = tg x, 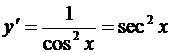 ;
;
9. 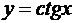 ,
, 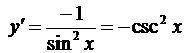 ;
;
10. 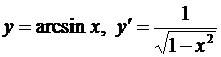 ;
;
11. 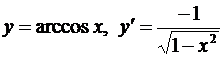 ;
;
12. 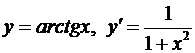 ; 13.
; 13. 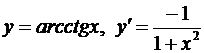 .
.
Из приведенной таблицы следует, что производная любой элементарной функции представляет собой также элементарную функцию. Таким образом, операция дифференцирования не выводит нас из класса элементарных функций.
§2. ДИФФЕРЕНЦИАЛ ЧИСЛОВОЙ ФУНКЦИИ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
Условие постоянства функции
Теорема.Если функция f(x) дифференцируема на интервале (a,b) и если всюду на этом интервале 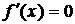 , то функция f(x) является постоянной на интервале (a,b).
, то функция f(x) является постоянной на интервале (a,b).
Доказательство. Пусть х0 – некоторая фиксированная точка интервала (a,b), а х – любая точка этого интервала.
Сегмент [х0,х] целиком принадлежит интервалу (a,b). Поэтому функция f(x) дифференцируема (а стало быть и непрерывна) всюду на сегменте [х0,х]. Это дает право применить к функции f(x) на сегменте [х0,х] теорему Лагранжа. Согласно этой теореме внутри сегмента [х0,х] найдется точка ξ такая, что
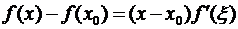 . (3.35)
. (3.35)
По условию производная функции f(x), равна нулю всюду в интервале (a,b). Стало быть, 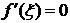 и из формулы (3.35) получаем
и из формулы (3.35) получаем 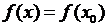 . Это и означает, что функция f(x) постоянна всюду на интервале (a,b).
. Это и означает, что функция f(x) постоянна всюду на интервале (a,b).
Данное утверждение имеет простой геометрический смысл: если касательная в каждой точке некоторого участка кривой у = f(x) параллельна оси Ох, то указанный участок кривой у = f(x) представляет собой отрезок прямой, параллельный оси Ох.
Формула Тейлора
Устанавливаемая в этом параграфе формула является одной из основных формул математического анализа и имеет многочисленные приложения, как в анализе, так и в смежных дисциплинах. Данная формула устанавливает способ приближенного отображения, или, как говорят, способы аппроксимации произвольной функции с помощью полиномов (многочленов), которые являются наиболее простыми среди всех других функций.
Предположим, что функция 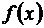 имеет все производные до (п + 1) порядка включительно в некотором промежутке, содержащем точку х = х0. Найдем многочлен Рп(х) степени не выше п, значение которого в точке х0 равняется значению функции
имеет все производные до (п + 1) порядка включительно в некотором промежутке, содержащем точку х = х0. Найдем многочлен Рп(х) степени не выше п, значение которого в точке х0 равняется значению функции 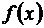 в этой точке, а значения его производных до п-го порядка в точке х = х0 равняются значениям соответствующих производных от функции
в этой точке, а значения его производных до п-го порядка в точке х = х0 равняются значениям соответствующих производных от функции 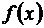 в этой точке.
в этой точке.
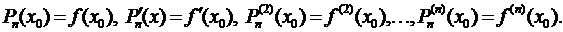 (3.43)
(3.43)
Естественно ожидать, что такой многочлен в некотором смысле «близок» к функции 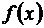 .
.
Будем искать этот многочлен в форме многочлена по степеням (х – х0) с неопределенными коэффициентами
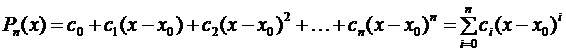 (3.44)
(3.44)
Неопределенные коэффициенты ci, i = 0, 1, 2, …, п определим так, чтобы удовлетворялись условия (3.43).
Предварительно найдем производные от Рп(х):
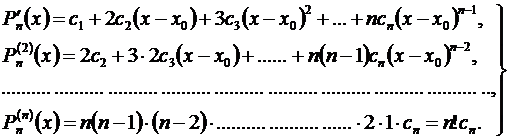 (3.45)
(3.45)
Подставляя в левые и правые части равенств (3.44) и (3.45) вместо х значение х0и заменяя на основании равенств (3.43) Рп(х0) через 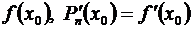 и т.д., получим:
и т.д., получим:
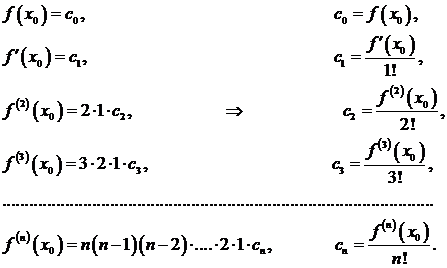
Подставляя найденные значения сi в формулу (3.44), получим искомый многочлен: 
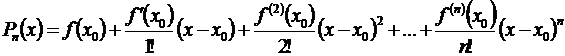 . (3.46)
. (3.46)
Многочлен (3.46) называют многочленом Тейлора для функции 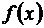 . Обозначим через Rn+1(х) разность значений данной функции
. Обозначим через Rn+1(х) разность значений данной функции 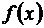 и построенного многочлена Pn(x): Rn+1(х) =
и построенного многочлена Pn(x): Rn+1(х) = 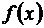 – Pn(x).
– Pn(x).
Откуда 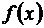 = Pn(x) + Rn+1(х), или, в развернутом виде:
= Pn(x) + Rn+1(х), или, в развернутом виде:
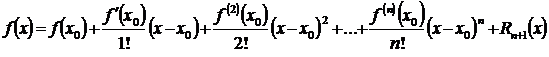 . (3.47)
. (3.47)
Выражение (3.47) называют формулой Тейлора для функции 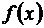 в окрестности точки х0, а Rn+1(х) – остаточным (дополнительным) членом формулы Тейлора. Для тех значений х, для которых остаточный член Rn+1(х) мал, многочлен Pn(x) дает приближенное значение функции
в окрестности точки х0, а Rn+1(х) – остаточным (дополнительным) членом формулы Тейлора. Для тех значений х, для которых остаточный член Rn+1(х) мал, многочлен Pn(x) дает приближенное значение функции 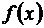 .
.
Таким образом, формула (3.47) дает возможность заменить функцию
у = 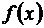 многочленом у = Pn(x) с соответствующей степенью точности, равной значению остаточного члена Rn+1(х). Можно показать, что такое представление функции
многочленом у = Pn(x) с соответствующей степенью точности, равной значению остаточного члена Rn+1(х). Можно показать, что такое представление функции 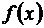 единственно, т.е., что, если имеем одновременно, вблизи х0,
единственно, т.е., что, если имеем одновременно, вблизи х0,
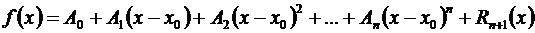 ,
,
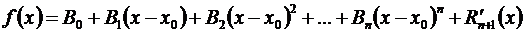 ,
,
то необходимо А0 = В0, А1 = В1,…, Ап = Вп.
Для остаточного члена получено довольно много различных форм представления, одно из которых имеет вид:
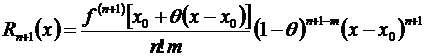 , (3.48)
, (3.48)
где т – произвольное положительное число, 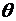 – число, заключенное в интервале (0,1) и зависит не только от х и п,но также и от т. Остаточный член, записанный в виде (3.48), принято называть остаточным членом в общей форме.
– число, заключенное в интервале (0,1) и зависит не только от х и п,но также и от т. Остаточный член, записанный в виде (3.48), принято называть остаточным членом в общей форме.
Из него, придавая т конкретные значения, можно получить более частные формы остаточного члена. Положив т = п + 1, получим остаточный член в форме Лагранжа:
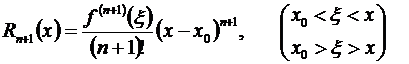 . (3.49)
. (3.49)
Он напоминает следующий очередной член формулы Тейлора, лишь вместо того, чтобы вычислять (п + 1)-ю производную в точке х0, эту производную берут для некоторого среднего (между х0 и х) значения 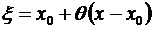 .
.
При т = 1 приходим к остаточному члену в форме Коши.
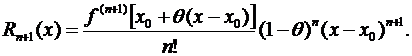 (3.50)
(3.50)
Так как формы Лагранжа и Коши отвечают разным значениям m, а θ зависит от m, то значения θ в формулах (3.49) и (3.50) является, вообще говоря, различными. Обе формы остаточного члена (Лагранжа и Коши) обычно используются в тех случаях, когда требуется при тех или иных фиксированных значениях х, отличных от х0, приближенно вычислить функцию 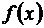 с наперед указанной степенью точности, которую можно оценить по формулам (3.49) и (3.50) для данного х, а также воздействовать на нее за счет изменения n. Наряду с этим встречаются задачи в которых нас интересует не численная величина указанной ошибки, а лишь порядок ее относительно малой величины (х – х0). Для этой цели удобна форма записи остаточного члена в виде
с наперед указанной степенью точности, которую можно оценить по формулам (3.49) и (3.50) для данного х, а также воздействовать на нее за счет изменения n. Наряду с этим встречаются задачи в которых нас интересует не численная величина указанной ошибки, а лишь порядок ее относительно малой величины (х – х0). Для этой цели удобна форма записи остаточного члена в виде
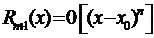 . (3.51).
. (3.51).
Данная формула означает, что при стремлении х к х0 остаточный член 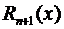 представляет собой бесконечно малую порядка выше n-го по сравнению с (х – х0), т.е.
представляет собой бесконечно малую порядка выше n-го по сравнению с (х – х0), т.е. 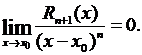 Равенство (3.51) называют остаточным членом, представленным в форме Пеано.
Равенство (3.51) называют остаточным членом, представленным в форме Пеано.
Формулу Тейлора (3.47) часто записывают в несколько ином виде. Положив в (3.47) (х – х0) = Δх, х = х0 + Δх и f (х) – f (х0) = Δf (х0) получаем
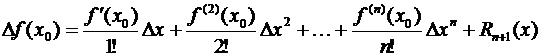 (3.52)
(3.52)
с точностью до дополнительного члена, таким образом, приращение функции разложено по степеням приращения независимой переменной.
Далее, вспоминая, что
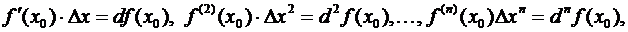
мы можем переписать (3.52) в такой форме
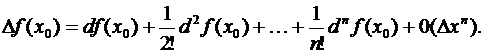
Здесь остаточный член записан в форме Пеано. Отсюда видим, что при 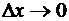 последовательные дифференциалы представляют собой, с точностью до факториалов в знаменателе, именно простейшие бесконечно малые члены соответственных порядков (относительно
последовательные дифференциалы представляют собой, с точностью до факториалов в знаменателе, именно простейшие бесконечно малые члены соответственных порядков (относительно 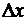 ) в разложении бесконечно малого приращения функции.
) в разложении бесконечно малого приращения функции.
Если в (3.52) остаточный член записать в форме Лагранжа (3.49), то формула Тейлора (3.52) с остаточным членом в форме Лагранжа (3.49) является естественным обобщением формулы Лагранжа (3.34). Формула Лагранжа (3.34) конечных приращений получается из формулы (3.52) в частном случае n = 0.
Аппроксимация функций
В этом разделе наряду с формулой Тейлора будет изложен еще один способ приближенного изображения (аппроксимации) функции с помощью полинома.
Пусть функция у = f(x) заданна на промежутке [a,b]. Выделим здесь произвольно п интерполяционных узлов x1, x2,…, xn.
Построим интерполяционный полином Лагранжа 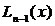 степени не выше n – 1, который бы в этих узлах приобретал те же значения, что и функция f(х), т.е.
степени не выше n – 1, который бы в этих узлах приобретал те же значения, что и функция f(х), т.е.
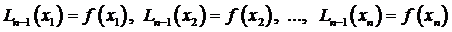 . (3.62)
. (3.62)
Интерполяционный полином Лагранжа 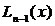 определяется равенством (3.61)
определяется равенством (3.61)
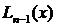 =
= 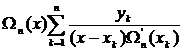 =
= 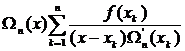 . (3.63)
. (3.63)
Свойства полинома Лагранжа 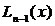 , выраженные равенствами (3.62), геометрически означают, что график полинома Лагранжа у =
, выраженные равенствами (3.62), геометрически означают, что график полинома Лагранжа у = 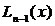 (рис.22, пунктирная кривая) имеет в интерполяционных узлах x1, x2,…, xn такие же ординаты, что и график функции y = f(x) (рис.22, сплошная кривая).
(рис.22, пунктирная кривая) имеет в интерполяционных узлах x1, x2,…, xn такие же ординаты, что и график функции y = f(x) (рис.22, сплошная кривая).
Поскольку полином Лагранжа 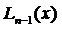 принимают за приближенное выражение для f(x),возникает потребность найти ошибку
принимают за приближенное выражение для f(x),возникает потребность найти ошибку 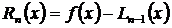 приближенного равенства
приближенного равенства 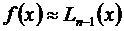 .
.
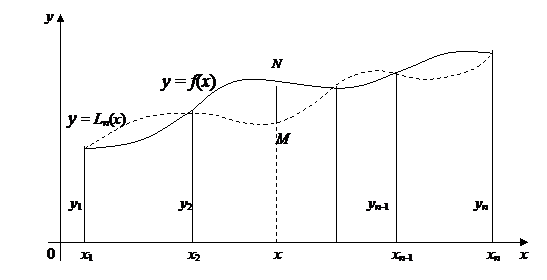
Рис. 22
Геометрическое значение 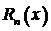 такое же, как и для остаточного члена формулы Тейлора:
такое же, как и для остаточного члена формулы Тейлора: 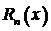 есть отрезок ординаты МN,расположенный между графиками функции f(х) и полинома
есть отрезок ординаты МN,расположенный между графиками функции f(х) и полинома 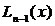 в точке х,взятой со знаком плюс, если график f(х) в точке х проходит выше графика
в точке х,взятой со знаком плюс, если график f(х) в точке х проходит выше графика 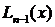 (рис.22), и со знаком минус, если ниже.
(рис.22), и со знаком минус, если ниже.
Теорема.Пусть на промежутке [a,b] для функции f(x)существуют последовательные производные 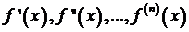 и пусть интерполяционные узлы
и пусть интерполяционные узлы 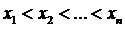 лежат в промежутке [a,b]. Тогда можно найти, по крайней мере, одну такую точку х = ξ, которая лежит в промежутке [a,b],что выполняется равенство
лежат в промежутке [a,b]. Тогда можно найти, по крайней мере, одну такую точку х = ξ, которая лежит в промежутке [a,b],что выполняется равенство
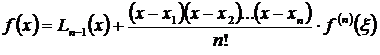 (3.64)
(3.64)
для всех х,которые лежат в промежутке [a,b].
Доказательство. Пусть точка х зафиксирована на промежутке [a,b] и не совпадает ни с одним из интерполяционных узлов. Рассмотрим вспомогательную функцию
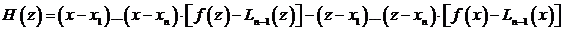 . (3.65)
. (3.65)
При этих условиях вспомогательная функция Н(z) имеет на [a,b] (n + 1) корней и будет обращаться в нуль на концах каждого из отрезков 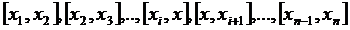 ,
,
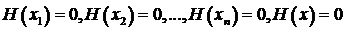 . (3.66)
. (3.66)
Применяя теорему Роля к каждому из этих отрезков убеждаемся, что производная 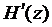 , имеет не менее п корней в п разных точках
, имеет не менее п корней в п разных точках 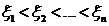 ,
,
расположенных внутри отрезков 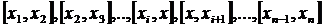 ,таких что
,таких что 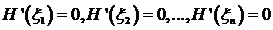 .
.
Применив теорему Ролля к производной 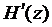 , мы убеждаемся, что производная
, мы убеждаемся, что производная 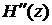 имеет п – 1 корней на [a,b]. Продолжая эти рассуждения, придем к заключению, что на рассматриваемом отрезке [a,b] производная
имеет п – 1 корней на [a,b]. Продолжая эти рассуждения, придем к заключению, что на рассматриваемом отрезке [a,b] производная 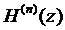 имеет хотя бы один корень, который обозначим через
имеет хотя бы один корень, который обозначим через 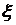 , т.е.
, т.е.
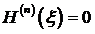 . (3.67)
. (3.67)
Найдем из (3.65) 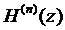 . Учитывая, что
. Учитывая, что 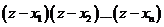 – полином степени п,а тогда, как установлено ранее,
– полином степени п,а тогда, как установлено ранее, 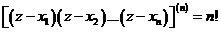 , имеем
, имеем
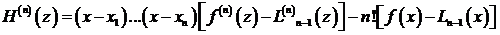 . (3.68)
. (3.68)
Далее, степень полинома 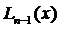 не выше п – 1, и потому
не выше п – 1, и потому 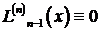 . Следовательно
. Следовательно
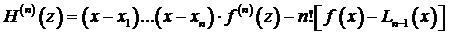 .
.
Отсюда находим
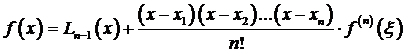 . (3.69)
. (3.69)
Причем, ξ не совпадает с узлами x1, x2,…, xn и точкой х. Теорема доказана.
Равенство (3.69) называется интерполяционной формулой Лагранжа с остаточным членом. Остаточный член Rn(x)в этой формуле определяется равенством
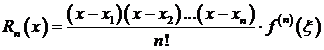 .
.
Отсюда, если известна верхняя граница 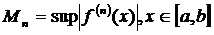 ,
,
получим оценку для абсолютной погрешности вычисления значений функции f(х) с использованием интерполяционной формулы Лагранжа
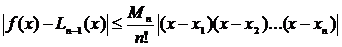 .
.
Из полученной оценки следует, что чем больше используется интерполяционных узлов, тем выше точность вычисления.
Пример. Функцию
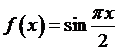 (3.70)
(3.70)
аппроксимировать с помощью интерполяционного полинома Лагранжа 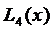 , который, в пяти узлах
, который, в пяти узлах 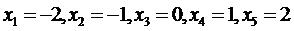 приобретал бы те же значения, что и заданная функция (3.70), и оценить точность этого приближения.
приобретал бы те же значения, что и заданная функция (3.70), и оценить точность этого приближения.
Прежде всего, вычислим значения этой функции в интерполяционных узлах. Из (3.70) находим
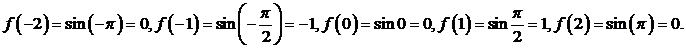 Следовательно, полином
Следовательно, полином 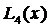 должен быть построен по таблице
должен быть построен по таблице
| x | –2 | –1 | |||
| y | –1 |
Поэтому
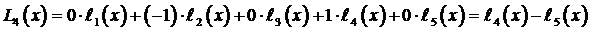 .
.
Для 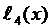 и
и 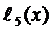 имеем
имеем
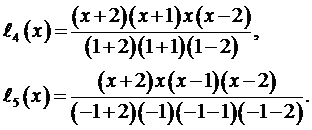
Таким образом,
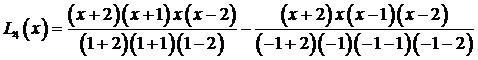
и после упрощений получаем 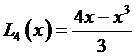 .
.
Далее, для остаточного члена R5(x)нужно вычислить 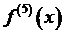 .
.
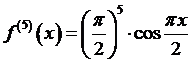 .
.
Поэтому для функции 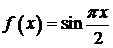 этого примера имеет место такая формула интерполяции Лагранжа с остаточным членом
этого примера имеет место такая формула интерполяции Лагранжа с остаточным членом
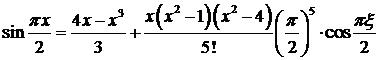 .
.
Если для вычисления значений функции 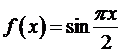 пользоваться приближенной формулой
пользоваться приближенной формулой 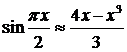 , то абсолютная погрешность такого вычисления, учитывая, что |
, то абсолютная погрешность такого вычисления, учитывая, что | 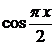 | ≤ 1 составит
| ≤ 1 составит
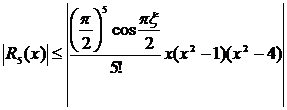
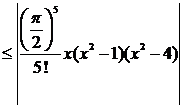 .
.
Так, для 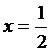 абсолютная погрешность вычисления составит
абсолютная погрешность вычисления составит
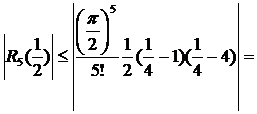 0,11.
0,11.
На рис.23 изображены графики функции 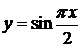 (сплошная кривая) и интерполяционного полинома
(сплошная кривая) и интерполяционного полинома 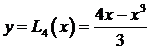 (пунктирная кривая).
(пунктирная кривая).
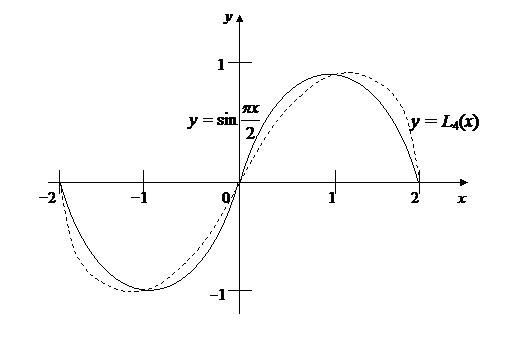
Рис. 23
Отметим, что 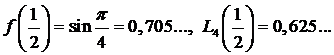 и абсолютная погрешность аппроксимации составляет 0,08.
и абсолютная погрешность аппроксимации составляет 0,08.
Для достижения более высокой точности вычисления необходимо
увеличивать число интерполяционных узлов.
Асимптоты
Очень часто приходится исследовать форму кривой y = f(x), а значит, и характер изменения соответствующей функции при неограниченном возрастании (по абсолютной величине) абсциссы x или ординаты y переменной точки М(x,y) кривой или абсциссы и ординаты одновременно. При этом важным частным случаем является тот, когда исследуемая кривая при удалении ее переменной точки М(x,y) в бесконечность (расстояние этой точки от начала координат неограниченно возрастает) неограниченно приближается к некоторой прямой.
Определение. Если рассеяние δ от точки кривой до некоторой определенной прямой по мере удаления точки в бесконечность стремится к нулю, то эта прямая называется асимптотой кривой (рис.26).
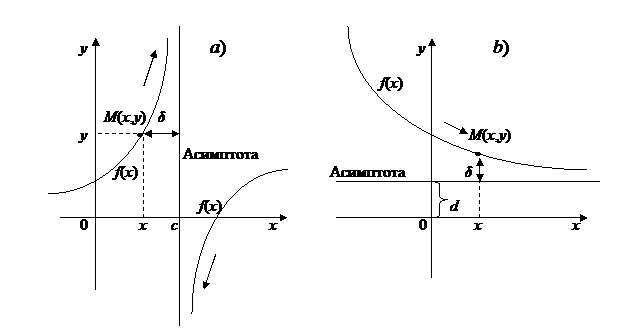
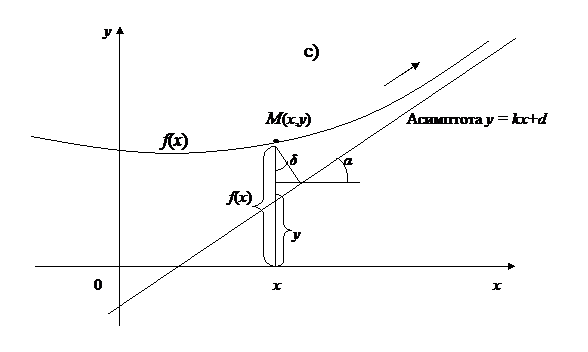
Рис. 26
Кривые с бесконечной ветвью могут иметь три вида асимптот: вертикальные (т.е. параллельные оси ординат, рис.26,а), горизонтальные (т.е. параллельные оси абсцисс, рис.26,b) и наклонные (рис.26,с).
Вертикальные асимптоты
Из определения асимптот следует, что если 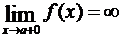 , или
, или 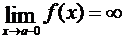 , или
, или 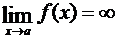 , то прямая x = a есть асимптота кривой y = f(x); и обратно, если прямая x = a есть асимптота, то выполняется одно из написанных равенств.
, то прямая x = a есть асимптота кривой y = f(x); и обратно, если прямая x = a есть асимптота, то выполняется одно из написанных равенств.
Следовательно, для отыскания вертикальных асимптот нужно найти такие значения x = a, при приближении к которым функция 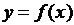 стремится к бесконечности. Тогда прямая x = a будет вертикальной асимптотой. Точкам x = a соответствуют разрывы функции f(x) второго рода. Например, кривая
стремится к бесконечности. Тогда прямая x = a будет вертикальной асимптотой. Точкам x = a соответствуют разрывы функции f(x) второго рода. Например, кривая 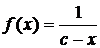 имеет вертикальную асимптоту x = с, так как
имеет вертикальную асимптоту x = с, так как 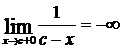 ;
; 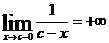 (или
(или 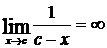 ).
).
В точке x = с функция 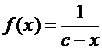 терпит разрыв второго рода (рис.26,а).
терпит разрыв второго рода (рис.26,а).
Горизонтальные асимптоты
Для того чтобы, например, при x → +∞, прямая y = d служила асимптотой для кривой f(x), очевидно (рис.26,b), необходимо и достаточно, чтобы было
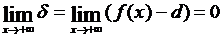 или
или 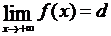 .
.
Таким образом, вопрос о горизонтальной асимптоте сводится попросту к вопросу об этом пределе.
Отдельно нужно искать подобный предел и при x → –∞; при этом может получиться и другая асимптота. Например, в случае кривой f(x) = arctg x (рис.8) имеем: 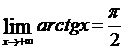 ;
; 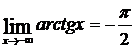 .
.
Следовательно, для кривой f(x) = arctg x,при x → +∞ асимптотой является прямая 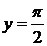 , а при x → –∞ – прямая
, а при x → –∞ – прямая 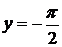 (рис.8).
(рис.8).
Наклонные асимптоты
Предположим, что кривая f(x) имеет наклонную асимптоту y = kx+d, например, со стороны положительной части оси Oх (рис.26,c). Определим числа k и d. Так как разность ординат 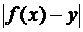 лишь постоянным множителем (равным косинусу угла между асимптотой и осью Oх) разнится от расстояния δ (
лишь постоянным множителем (равным косинусу угла между асимптотой и осью Oх) разнится от расстояния δ ( 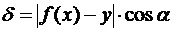 , рис.26,с), то при x → +∞ одновременно с δ должна стремится к нулю и эта разность.
, рис.26,с), то при x → +∞ одновременно с δ должна стремится к нулю и эта разность.
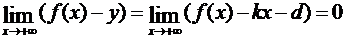 . (3.71)
. (3.71)
Разделив на x, получим отсюда:
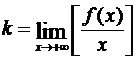 (так как
(так как 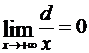 ). (3.72)
). (3.72)
Зная k, из равенства (3.71) находим d:
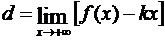 . (3.73)
. (3.73)
Итак, для того чтобы прямая y = kx + d была асимптотой для данной кривой, необходимо выполнение условий (3.72) и (3.73). Обратное рассуждение покажет и их достаточность. Вопрос здесь сведется к последовательному разысканию пределов (3.72) и (3.73), которыми уже и определятся коэффициенты уравнения прямой y = kx + d, удовлетворяющей равенству (3.71) и, следовательно, обладающей свойством асимптоты.
Мы проводили исследования при x → +∞, но все рассуждения справедливы и при x → –∞. Поэтому для случая x → –∞ нужно повторить все исследование. При этом может получиться и другая асимптота по сравнению со случаем x → +∞. Например, в случае функции 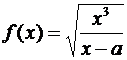 имеем при x → +∞
имеем при x → +∞
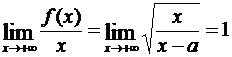 ,
,
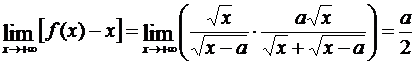 ,
,
так что, со стороны положительных значений x, кривая приближается к асимптоте 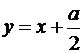 . Со стороны же отрицательных x получается другая асимптота
. Со стороны же отрицательных x получается другая асимптота 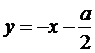 . Действительно, при x → –∞ имеем
. Действительно, при x → –∞ имеем
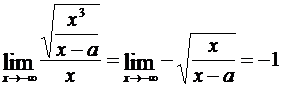 ,
,

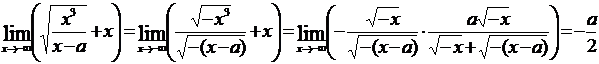 .
.
УПРАЖНЕНИЯ
1. Найти производные следующих функций:
а) 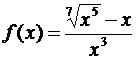 ; б)
; б) 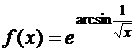 ; в)
; в) 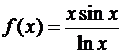 ;
;
г) 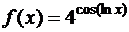 ; д)
; д) 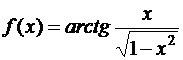 ; е)
; е) 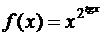 ;
;
ж) 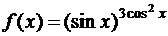 .
.
2. Найти производные следующих функций, заданных неявно:
а) 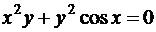 ; б)
; б) 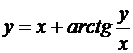 ; в)
; в) 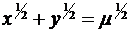 ,
,  .
.
3. Найти уравнение касательной и нормали к кривым второго порядка, проходящих через точку М0 (x0, y0) и лежащую на этих кривых:
а) 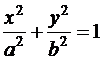 – эллипс; б)
– эллипс; б) 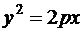 – парабола.
– парабола.
4. Найти производные 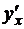 следующих функций, заданных параметрически:
следующих функций, заданных параметрически:
а) 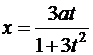 ,
, 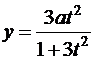 ; б)
; б) 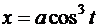 ,
, 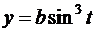 ;
;
в) 
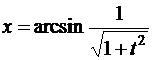 ,
, 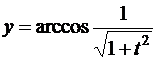 .
.
5. Проверить выполнение условий теоремы Лагранжа (частный случай Ролля) для функций:
а) 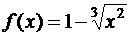 , на отрезке [–1,1]; б)
, на отрезке [–1,1]; б) 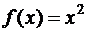 , xÎ[0,1];
, xÎ[0,1];
в) 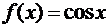 ,
, 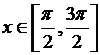 и xÎ[0, π].
и xÎ[0, π].
Если функция удовлетворяет условиям теоремы, найти промежуточное значение ξ.
6. Пользуясь правилом Лопиталя вычислить следующие пределы:
а) 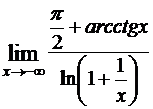 ; б)
; б) 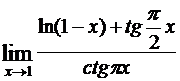 ; в)
; в) 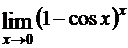 ;
;
г) 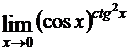 ; д)
; д) 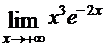 .
.
7. Используя формулу Тейлора вычислить с точностью до 0.001 следующие значения:
а) 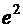 ; б)
; б) 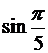 ; в)
; в) 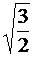 ; г)
; г) 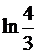 .
.
8. Найти наибольшее и наименьшее значения функций:
а)