Классическое определение вероятности событий
Основные понятия теории вероятностей. Основные теоремы теории вероятностей. Схема повторных испытаний (4 ч)
Основные понятия теории вероятностей
1. В урне находится 12 пронумерованных шаров. Опыт состоит в извлечении одного из них.
а) Приведите пример достоверных, невозможных и случайных событий при данном испытании.
б) Найдите полную группу событий.
в) Определите элементарные события, благоприятные событиям:
А={появление шара с нечётным номером};
В={появление шара с чётным номером};
C={ появление шара с номером большим 3};
D={ появление шара с номером меньшим 7};
г) Какие из событий А, В, С, D являются попарно совместными?
д) Найдите события, противоположные событиям А, В, С, D.
2. Какие из следующих событий являются совместными?
а) А={ Выход из строя телевизора, работающего на кухне} и В={Выход из строя телевизора, работающего в гостиной}
б) C={ попадание при одном выстреле} и D={промах при одном выстреле}
в) Е={ хотя бы одно попадание при двух выстрелах}
и D={ два попадания при двух выстрелах };
3. Три студента решают задачу. Обозначим события:
А ={задачу решил первый студент };
В = {задачу решил второй студент };
C = {задачу решил третий студент }.
Выразить через А, В, С события:
D={ все студенты решили задачу},
Е={задачу решил только первый студент};
F = {задачу решил хотя бы один студент},
К = { задачу решил только один студент }.
4. В корзине розы разных цветов.
Событие А ={выбрана красная роза}; В = {выбрана белая роза}.
Что означают события: а) 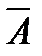 , б)
, б) 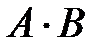 , в)
, в) 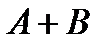 , г)
, г) 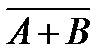 , д)
, д) 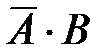 , е)
, е) 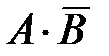
5. Событие С благоприятно событию D. Что представляет собой события: а) С+D, б) 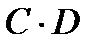 , в)
, в) 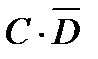 ?4
?4
Случайные величины и их законы распределения (4 ч)
Дискретная случайная величина.
1. Найти математическое ожидание М(x), дисперсию D(x) и среднее квадратическое отклонение случайной величины X, если закон её распределения задан таблицей
| x | |||
| p | 0,25 | 0,6 | 0,15 |
2. Случайная величина X – число выпавших орлов при подбрасывании двух монет.
а) Составить закон распределения случайной величины Х.
б) найти функцию распределения F(x) и построить её график.
3. Вероятность отказа в работе сигнального устройства, равна 0,05. На предприятии три таких устройства. Составить закон распределения случайной величины Х-«число сигнальных устройств, вышедших из строя», найти М(Х), D(Х) и σ(Х).
4. Вероятность нарушения герметичности банки консервов равна 0,004. а) найти вероятность того, что из 500 таких консервов герметичность нарушена не менее чем у трёх банок;
б) найти М(Х) и D(Х) случайной величины X-«число банок консервов, потерявших герметичность».
5. На заводе работают три автоматические линии. В течение рабочей смены первая линия не потребует ремонта с вероятностью 0,9, вторая- с вероятностью 0,8, а третья- с вероятностью 0,75. Составить закон распределения числа линий, которые в течение смены потребуют ремонта. Найти среднее квадратическое отклонение этой величины.
| Х | |||
| Р | 0,25 | 0,5 | 0,25 |
Ответы:
1. М(Х)=1,05; D(Х)=0,85 ; σ(Х)=0,92.
2. а) Закон распределения:
б)
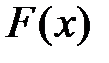
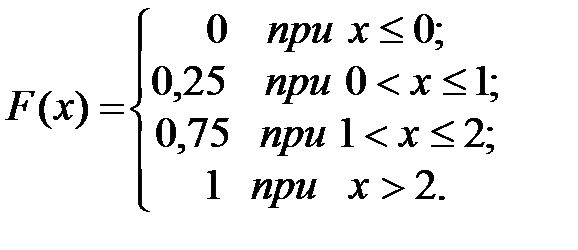
0 1 2 3 х
| Х | ||||
| Р | 0,857375 | 0,135375 | 0,007125 | 0,000125 |
3.
М(Х)=0,15; D(Х)=0,14; σ(Х)=0,38.
4. 0,315.
| Х | ||||
| Р | 0,540 | 0,375 | 0,08 | 0,005 |
5. σ (Х)= 0,67;
X 2 5 8 x
в) Р(-4<Х<14)=0,9974
5)0,6826; 6).а) 492; б) 143.
Ответы. 1.
2.0,43.
Основные понятия теории вероятностей. Основные теоремы теории вероятностей. Схема повторных испытаний (4 ч)
Основные понятия теории вероятностей
1. В урне находится 12 пронумерованных шаров. Опыт состоит в извлечении одного из них.
а) Приведите пример достоверных, невозможных и случайных событий при данном испытании.
б) Найдите полную группу событий.
в) Определите элементарные события, благоприятные событиям:
А={появление шара с нечётным номером};
В={появление шара с чётным номером};
C={ появление шара с номером большим 3};
D={ появление шара с номером меньшим 7};
г) Какие из событий А, В, С, D являются попарно совместными?
д) Найдите события, противоположные событиям А, В, С, D.
2. Какие из следующих событий являются совместными?
а) А={ Выход из строя телевизора, работающего на кухне} и В={Выход из строя телевизора, работающего в гостиной}
б) C={ попадание при одном выстреле} и D={промах при одном выстреле}
в) Е={ хотя бы одно попадание при двух выстрелах}
и D={ два попадания при двух выстрелах };
3. Три студента решают задачу. Обозначим события:
А ={задачу решил первый студент };
В = {задачу решил второй студент };
C = {задачу решил третий студент }.
Выразить через А, В, С события:
D={ все студенты решили задачу},
Е={задачу решил только первый студент};
F = {задачу решил хотя бы один студент},
К = { задачу решил только один студент }.
4. В корзине розы разных цветов.
Событие А ={выбрана красная роза}; В = {выбрана белая роза}.
Что означают события: а) 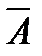 , б)
, б) 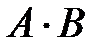 , в)
, в) 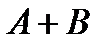 , г)
, г) 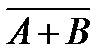 , д)
, д) 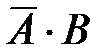 , е)
, е) 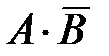
5. Событие С благоприятно событию D. Что представляет собой события: а) С+D, б) 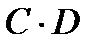 , в)
, в) 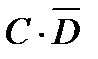 ?4
?4
Классическое определение вероятности событий
1. Испытание состоит в бросании игральной кости.
Найти вероятность того, что число выпавших очков:
а) будет равно шести; б) будет кратно трём; в). будет меньше единицы; г) не превысит шести .
2. Бросаются две монеты. Найти вероятность событий :
А= «хотя бы на одной из монет выпадет орёл», В= «орел не выпадет ни на одной», Е= «выпадет орёл только на одной монете».
3. Брошены 2 игральные кости. Найти вероятность того, что
а) произведение выпавших очков окажется большим 20,
б) что сумма выпавших очков будет равна 6.
4. В колоде 36 карт. Вынимают наугад одну карту. Какова вероятность того, что эта карта окажется а) тузом,б) червовой масти, в) старше валета?
5. Из 40 экзаменационных вопросов студент выучил 30. Какова вероятность того, что а) он ответит на заданный вопрос, б) он ответит на два заданных вопроса, в) студент ответит на два из трёх заданных вопроса?
6 .Имеется шесть одинаковых карточек с буквами Н, М, И, Я, Л, О. Найти вероятность того, что:
а) при извлечении произвольным образом трёх карточек получится слово «ЛОМ»,
б) при извлечении шести карточек получится слово «МОЛНИЯ»?
7. Десять различных книг расставляются наудачу на одной полке. Найти вероятность того, что три определённые книги окажутся рядом.
8. Первенство по футболу оспаривают 18 команд, среди которых 5 лидирующих. Путём жеребьёвки команды распределяются на две группы по 9 команд в каждой.
а) Какова вероятность попадания всех лидирующих команд в одну группу (событие А)?
б) Какова вероятность попадания двух лидирующих команд в одну группу, а трёх в другую (событие В)?
9. В урне 5 белых и 7 чёрных шаров. Из урны одновременно вынимают два шара. Найти вероятность того, что извлечённые шары:
а) оба белые, б) оба чёрные, в) один белый и один чёрный
10. В урне а белых и в чёрных шаров. Из урны одновременно вынимают k шара. Напишите формулу для вычисления вероятности того, что среди них будет d белых, и следовательно, k-d чёрных.
Ответы:
1. а)1/6, б) 1/3; в) 0; г) 1. 2. P(A)=0,75; P(B)=0,25; P(E)=0,5. 3.а)1/6; б) 5/36; 4. а) 1/9; б) 1/4; в) 1/3. 5. а) 0,75; б) 0,56; в) 0,44. 6. а) 0,008; б) 0,0014. 7. 0,067. 8. а) 0,002; б) 0,075. 9. а) 5/33; б) 7/22; в) 35/66. 10.