Раздел 5. оператор цикла с параметром
5.1. Напечатать ряд чисел 20 в виде: 20 20 20 20 20 20 20 20 20 20.
5.2. Составить программу вывода любого числа - заданное число раз в виде, аналогичном показанному в предыдущей задаче.
5.3. Напечатать "столбиком":
а) все целые числа от 20 до 35;
б) квадраты всех целых чисел от 10 до В (значение В вводится с клавиатуры; В 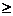 10);
10);
в) третьи степени всех целых чисел от А до 50 (значение А вводится с клавиатуры; А  50);
50);
г) все целые числа от А до В (значения А и В вводятся с клавиатуры; В 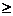 А).
А).
5.4. Напечатать числа следующим образом:
10 10.4 25 25.5 24.8
11 11.4 26 26.5 25.8
… …
25 25.4 35 35.5 34.8
а б
5.5. Напечатать числа следующим образом:
21 20.4 16 15.5 16.8
22 21.4 17 16.5 17.8
… …
35 34.4 24 23.5 24.8
а б
5.6. Одна штука некоторого товара стоит 20,4 руб. Напечатать таблицу стоимости 2, 3, ..., 20 штук этого товара
5.7. Напечатать таблицу соответствия между весом в фунтах и весом в килограммах для значений 1, 2, ..., 10 фунтов (1 фунт = 453 г).
5.8. Напечатать таблицу перевода расстояний в дюймах в сантиметры для значений 10, 11, ..., 22 дюйма (1 дюйм = 25,4 мм).
5.9. Считая, что Земля — идеальная сфера с радиусом R = 6350 км, определить расстояние до линии горизонта от точки с высотой над Землей, равной 1, 2, ..., 10 км.
5.10. Напечатать таблицу перевода 1, 2, ..., 20 долларов США в рубли по текущему курсу (значение курса вводится с клавиатуры).
5.11. Плотность воздуха убывает с высотой по закону
р = р0 е-bz,
где р — плотность на высоте bметров,
р =1,29 кг/м3,
z = 1,25*10-4.
Напечатать таблицу зависимости плотности от высоты для значений от 0 до 1000 м через каждые 100 м.
5.12. Составить таблицу умножения на 7.
5.13. Составить таблицу умножения на 9.
5. 14. Составить таблицу умножения на число n(значение n вводится с клавиатуры; 1  n
n  9).
9).
5.15. Напечатать "столбиком" значения sin2, sin3, ..., sin 20.
5.16. Рассчитать значения у для значений х, равных 4,5,...,28:
у = 2t2 + 5,5t — 2,
t= x + 2.
5.17. Рассчитать значения z для значений а, равных 2, 3, ..., 17:
z = 3,5t2 — 7t+ 16,
t= 4a.
5.18. Вывести "столбиком" значения sin0,1; sin0,2; ..., sin1,1.
5.19. Вывести "столбиком" значения 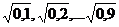
5.20. Напечатать таблицу стоимости 50, 100, 150, ..., 1000 г сыра (стоимость 1 кг сыра вводится с клавиатуры).
5.21. Напечатать таблицу стоимости 100, 200, 300, ...,2000 г конфет (стоимость 1 кг конфет вводится с клавиатуры) .
5.22. Вывести "столбиком" следующие числа: 2,1; 2,2; 2,3; ...,2,8.
5.23. Вывести "столбиком" следующие числа: 3,1; 3,2; 3,3; ... 3,9.
5.24. Вывести "столбиком" следующие числа: 2,2;2,4; 2,6; ... 4,2.
5.25. Вывести "столбиком" следующие числа: 4,4; 4,6; 4,8; ... 6,4.
5.26.Найти:
а) сумму всех целых чисел от 100 до 500;
б) сумму всех целых чисел от А до 500 (значение А вводится с клавиатуры; А  500);
500);
в) сумму всех целых чисел от - 10 до В (значение В вводится с клавиатуры; В 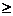 — 10);
— 10);
г) сумму всех целых чисел от А до В (значения А и В вводятся с клавиатуры; B 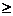 А).
А).
5.27. Даны натуральные числа х и у. Вычислить произведение x*у, используя лишь операцию сложения. Задачу решить двумя способами.
5.28. Найти:
а) произведение всех целых чисел от 8 до 15;
б) произведение всех целых чисел от А до 20 (значение А вводится с клавиатуры; 1  А
А  20);
20);
в) произведение всех целых чисел от 1 до В (значение В вводится с клавиатуры; 1  В
В  20);
20);
г) произведение всех целых чисел от А до В(значения А и В вводятся с клавиатуры; В 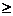 А).
А).
5.29. Найти:
а) среднее арифметическое всех целых чисел от 1 до 1000;
б) среднее арифметическое всех целых чисел от 100 до В(значение В вводится с клавиатуры; В 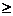 100);
100);
в) среднее арифметическое всех целых чисел от А до 200 (значение А и В вводится с клавиатуры; А  200);
200);
г) среднее арифметическое всех целых чисел от А до В (значения А и В вводятся с клавиатуры; В 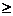 А).
А).
5.30.Найти:
а) сумму кубов всех целых чисел от 20 до 40;
б) сумму квадратов всех целых чисел от А до 50 (значение А вводится с клавиатуры; 0  А
А  50);
50);
в) сумму квадратов всех целых чисел от 1 до n(значение nвводится с клавиатуры; 1 < n < 100);
г) сумму квадратов всех целых чисел от А до В (значения А и В вводятся с клавиатуры; В 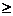 А).
А).
5.З1. Дано натуральное число n. Найти сумму n2+ (n + 1)2+ ... + (2n)2.
5.З2. Найти сумму — 12+ 22 — 32+ 42+ ... + 102. Условный оператор не использовать.
5.33. Найти сумму 22+ 23+ 24+ . + 210 . Операцию возведения в степень не использовать.
5.34. Вычислить сумму 1+1/2+1/3+…+1/n
5.35. Вычислить сумму 2/3+3/4+4/5+…+10/11
5.36. Вычислить сумму 1+1/3 +1/32 +… 1/38 . Операцию возведения в степень не использовать.
5.37. Вычислить сумму 1 — 1/2+1/3-…+(-1)n+1 1/n
Условный оператор и операцию возведения в степень не использовать.
5.38. Вычислить сумму x+x3/5+x5/5+…+x11/11 — при x
= 2.
5.39.Вычислить сумму 1 —2/3 x + 3/4x 2— 4/5х3 +...+ 11/12х10 при x= 2.
5.40. Вычислить значение выражения (( …(202 -192) – 182)2-…- 12)2
5.41.Дано пятизначное число. Найти число, получаемое при прочтении его цифр справа налево.
5.42. Составить программу возведения натурального числа в квадрат, учитывая следующую закономерность:
12= 1
22= 1+ 3,
32= 1+ 3+ 5,
42= 1+ 3+ 5+ 7,
…
n2=1+ 3+ 5+ 7+ 9+ ...+ (2n — 1).
5.43. Найти сумму 12+ 22+ 32+ ... + 102. Операцию возведения в степень не использовать, а учесть особенности получения квадрата натурального числа, отмеченные в предыдущей задаче.
5.44. Составить программу возведения натурального числа в третью степень, учитывая следующую закономерность:
13= 1,
23= 3+ 5,
33= 7+ 9+ 11,
43 = 13 + 15+ 17+ 19,
53 = 21 + 23 + 25 + 27 + 29.
5.45. Дано вещественное число аи натуральное число n. Вычислить значения а1, а2, а3, ..., аn.Операцию возведения в степень не использовать.
5.46. Составить программу для расчета факториала натурального числа n (факториал числа n равен 1* 2* ... *n).
5.47. В некоторых языках программирования (например, в Паскале) не предусмотрена операция возведения в степень. Составить программу для расчета степени n вещественного числа а (n — натуральное число).
5.48. Одноклеточная амеба каждые 3 часа делится на 2 клетки. Определить, сколько клеток будет через 3, 6, 9, ..., 24 часа, если первоначально была одна амеба.
5.49. Гражданин 1 марта открыл счет в банке, вложив 1000 руб. Через каждый месяц размер вклада увеличивается на 2% от имеющейся суммы. Определить:
а) прирост суммы вклада за первый, второй, ..., десятый месяц;
б) сумму вклада через три, четыре, ..., двенадцать месяцев.
5.50. Начав тренировки, лыжник в первый день пробежал 10 км. Каждый следующий день он увеличивал пробег на 10% от пробега предыдущего дня. Определить:
а) пробег лыжника за второй, третий, ..., десятый день тренировок;
б) какой суммарный путь он пробежал за первые 7 дней тренировок.
5.51. В некотором году (назовем его условно первым) на участке в 100 гектаров средняя урожайность ячменя составила 20 центнеров с гектара. После этого каждый год площадь участка увеличивалась на 5%, а средняя урожайность — на 2%. Определить:
а) урожайность за второй, третий, ..., восьмой год;
б) площадь участка в четвертый, пятый, ..., седьмой год;
в) какой урожай будет собран за первые шесть лет.
5.52. Определить суммарный объем в литрах 12 вложенных друг в друга шаров со стенками толщиной 5 мм. Внутренний диаметр внутреннего шара равен 10 см. Принять, что шары вкладываются друг в друга без зазоров.
5.53. Вычислить сумму 1! + 2! + 3! + ... + n!(значение nвводится с клавиатуры; 1 < n  10).
10).
5.54. Вычислить сумму 1+ 1/1!+ 1/2!+ 1/3! + ... +1/n!
где k! = 1*2*3*....*k. Значение n вводится с клавиатуры (1 < n <  10).
10).
5.55. Вычислить сумму
1+x1/1! +x2/2! +x3/3! +… +xn! , где k!=1* 2*3* ... *k
Значение nвводится с клавиатуры (1 < n  10).
10).
5.56. Вычислить сумму 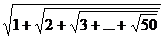
5.57. Дано натуральное число n, вычислить:
а) 1/sin1+1/ (sin1+ sin 2)+…+1/ (sin 1+ ... + sin n)
б) 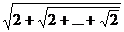 (n слагаемых)
(n слагаемых)
в)cos 1/sin1+(cos 1+ cos 2)/(sin1+sin2)+…+(cos1+ ... +cos n)/(sin1+ ....+ sin2n)
г) 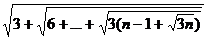
5.58. Около стены наклонно стоит палка длиной 4,5 м. Один ее конец находится на расстоянии 3 м от стены. Нижний конец палки начинает скользить в плоскости, перпендикулярной стене. Определить значение угла между палкой и полом (в градусах) с момента начала скольжения до падения палки через каждые 0,2 м.
Рекуррентные соотношения
5.59.Последовательность чисел а0, а1, а2, ...образуется по закону:
а0=1; аk= kak-1 + 1/k (k = 1,2, ...).
Дано натуральное число n. Получитьа1, а2..., аn .
5.60. Последовательность Фибоначчи образуется так: первый и второй члены последовательности равны 1, каждый следующий равен сумме двух предыдущих (1, 1, 2, 3, 5, 8, 13, ...). Дано натуральное число n (n 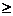 3).
3).
а) Найти k-й член последовательности Фибоначчи.
б) Получить первые nчленов последовательности Фибоначчи.
в) Верно ли, что сумма первых nчленов последовательности Фибоначчи есть четное число?
5.61. Рассмотрим последовательность, образованную дробями: 1/1, 2/1, 3/2, ..., в которой числитель (знаменатель) следующего члена последовательности получается сложением числителей (знаменателей) двух предыдущих членов. Числители двух первых дробей равны 1 и 2, знаменатели — 1 и 1.
а) Найти k-й член этой последовательности.
б) Получить первые nчленов этой последовательности.
в) Верно ли, что сумма первых nчленов этой последовательности больше числа A?
5.62. Последовательность чисел v0, v1, v2... образуется по закону: v1 = v2= 0; v3 = 1,5.
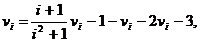 i= 4,5,…
i= 4,5,…
Дано натуральное число n (n 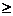 4). Получить vn .
4). Получить vn .
Площадь под кривой
5.63. Вычислить приближенно площадь одной арки синусоиды.
5.64. Вычислить приближенно площадь фигуры, образованной кривой у = 0,3(х — 1)2+ 4, осью абсцисс и двумя прямыми у = 1 и у = 3.
5.65. Вычислить приближенно площадь фигуры, образованной кривой у = 0,5(х + 1)2+ 2, осью абсцисс, осью ординат и прямой у = 2.
Ввод и обработка данных
5.66. Даны числа а1, а2 … а10 . Определить их сумму.
5.67. Даны натуральное число nи вещественные числа а1, а2 … аn
Определить сумму этих вещественных чисел.
5.68. Известна масса каждого из 12 предметов. Определить общую массу всего набора предметов.
5.69. Известны оценки абитуриента на четырех экзаменах. Определить сумму набранных им баллов.
5.70. В ведомости указана зарплата, выплаченная каждому из сотрудников фирмы за некоторый месяц. Определить общую сумму выплаченных по ведомости денег.
5.71. Известна масса каждого предмета, загружаемого в автомобиль. Определить общую массу груза.
5.72. Известно сопротивление каждого из элементов электрической цепи. Все элементы соединены последовательно. Определить общее сопротивление цепи.
5.73. Известно сопротивление каждого из элементов электрической цепи. Все элементы соединены параллельно. Определить общее сопротивление цепи.
5.74. Даны числа а1, а2 … а6. Определить их произведение.
5.75. Даны числа а1, а2 … а10 . Определить сумму их квадратов.
5.76. Даны натуральное число nи вещественные числа а1, а2 … аn.Определить сумму квадратов вещественных чисел.
5.77. Даны числа а1, а2 … а10.Определить их среднее арифметическое.
5.78. Даны натуральное число nи вещественные числа а1, а2 … аn.Определить среднее арифметическое вещественных чисел.
5.79. Известны оценки по физике каждого из 20 учеников класса. Определить среднюю оценку.
5.80. Известны оценки ученика по 10 предметам. Определить среднюю оценку.
5.81. Известны оценки по алгебре каждого ученика класса. Определить среднюю оценку.
5.82. Известна масса каждого предмета из некоторого набора предметов. Определить среднюю массу.
5.83. Даны натуральное число n и числа а1, а2 … аn.Определить:
а) 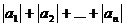
б) 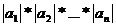
в) a1+a2, a2+a3, …,an-1 +an
г) а1 — а2 + а3 — ... + ( — 1)n+1аn.
Условный оператор и операцию возведения в степень не использовать.
5.84. Известны оценки двух учеников по четырем предметам. Определить сумму оценок каждого ученика.
5.85. Известны результаты двух спортсменов- пятиборцев в каждом из пяти видов спорта в баллах. Определить сумму баллов, полученных каждым спортсменом.
5.86. Известен возраст (количество лет, например, 14,5 лет) каждого ученика двух классов. Определить средний возраст учеников каждого класса. В каждом классе учатся 20 человек.
5.87. Известно количество осадков, выпавших за каждый день января и марта. Определить среднедневное количество осадков за каждый месяц.
5.88. Известен рост каждого ученика двух классов. Определить средний рост учеников каждого класса. Численность обоих классов одинаковая.
5.89. Известны оценки по физике каждого ученика двух классов. Определить среднюю оценку в каждом классе. Количество учащихся в каждом классе одинаковое.
5.90. В области 10 районов. Заданы площади, засеваемые пшеницей (в гектарах), и средняя урожайность (в центнерах с гектара) в каждом районе. Определить количество пшеницы, собранное в области, и среднюю урожайность по области.
5.91. В области 12 районов. Известны количество жителей (в тысячах человек) и площадь (в км2) каждого района. Определить среднюю плотность населения по области в целом.
5.92. В области 12 районов. Известны количество жителей каждого района (в тысячах человек) и плотность населения в нем (тыс. чел./ км2). Определить общую площадь территории области.
