Несколько условных операторов

4.30. Определить, является ли число А делителем числа В? А наоборот?

4.31. Составить программу для вычисления значения функции у (х):

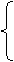kx, если k < x

y=

k+x, если k ³ x

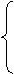x², если sin (x) < 0

где k =

|x|, если sin (x) ³ 0

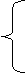4.32. Составить программу для вычисления значения функции f(x):

|x|, если x < 1

y=

kx, если k ³ x

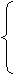x², если sin (x) ³ 0

где k =

|x|, если sin (x) < 0

4.33. Дано натуральное число.

а) Верно ли, что оно заканчивается нечетной цифрой?

б) Верно ли, что оно заканчивается четной цифрой?

В обеих задачах составные условия не использовать.

4.34. Даны два прямоугольника, стороны которых параллельны или перпендикулярны осям координат. Известны координаты левого нижнего угла каждого из них и длины их сторон. Один из прямоугольников назовем первым, другой — вторым. Найти координаты левого нижнего и правого верхнего углов минимального прямоугольника, содержащего указанные прямоугольники.

4.35. Даны цифры двух десятичных целых чисел: трехзначного а₃ а₂ а₁, и двузначного b₂ b₁ где а₁, и b₁,— число единиц, а₂ и b₂ — число десятков, а₃, — число сотен. Получить:

a) цифры, составляющие сумму этих чисел;

б) цифры, составляющие разность этих чисел со сложным условием

4.З6. Дано вещественное число х. Вычислить f(x), если:

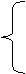x², при –2,4≤x≤5,7

ƒ=

4, в противном случае

4.37. Дано вещественное число х. Вычислить у(х),если:

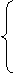sin (x), при 0,2<x<0,9

у=

1, в противном случае

4.38. Проверить, принадлежит ли число, введенное
с клавиатуры, интервалу (— 5, 3).

4.39. Определить, попадает ли точка с заданными
координатами в область 1 (для простоты принять, что
точка не попадает на границу этой области).

y

I

0 5 x

y

-2 I

0 x

-3

I

4.40 определить, попадает ли точка с заданными координатами в одну из областей I или II (для простоты принять, что абсцисса точки не равна 5):

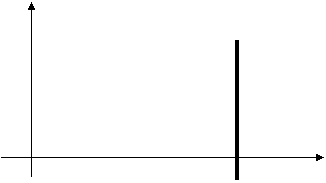y

II I

0 5 x

4.41. Даны три вещественных числа а, b, с. Проверить:

а) выполняется ли неравенство а < b < с;

б) выполняется ли неравенство b > а > с.

4.42. Определить, является ли число А делителем числа В или, наоборот, число В делителем числа А. Ответом должны служить сообщения: "Да, одно из чисел является делителем другого: или Нет, ни одно из чисел не является делителем другого.

4.43. Определить, верно ли, что при делении неотрицательного целого числа а на положительное число 6 получается остаток, равный одному из двух заданных чисел с или d.

4.44 Даны три вещественных числа а, b, с. определить имеется ли среди них хотя бы одна пара равных между собой чисел.

4.45. Определить, является ли треугольник со сторонами а, b, с равнобедренным.

4.46. Определить, является ли треугольник со сторонами а,b, с равносторонним.

4.47 Известен рост трех человек. Определить, одинаков ли их рост.

4.48 Год является високосным, если его номер кратен 4, однако из кратных 100 високосными являются лишь кратные 400 (например, 1700, 1800 и 1900 – не високосные года, 2000 - високосный). Дано натуральное число N. Определить, является ли високосным год с таким номером.

4.49. Даны вещественные положительные числа а, b, с. Выяснить, существует ли треугольник со сторонами а, b, с.

4.50 Даны вещественные положительные числа а, b, c, d. Выяснить можно ли прямоугольник со сторонами а, b, уместить внутри прямоугольника со сторонами c, d так, чтобы каждая из сторон одного прямоугольника была параллельна или перпендикулярна каж-дой стороне второго прямоугольника.

4.51. Даны вещественные положительные числа а, b, с, х, у. Выяснить, пройдет ли кирпич с ребрами
а, b, св прямоугольное отверстие со сторонами х и у. Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его ребер было параллельно или перпендикулярно каждой из сторон отверстия.

4.52. Поле шахматной доски определяется парой натуральных чисел, каждое из которых не превосходит восьми: первое число — номер вертикали (при счете слева направо), второе — номер горизонтали (при счете снизу вверх). Даны натуральные числа а, b, с, d, каждое из которых не превосходит восьми.

a) на поле (а, b) расположена ладья. Определить, угрожает ли она полю (с, d);

б) на поле (а, b ) расположен слон. Определить, угрожает ли он полю (c, d);

в) на поле (а, b)расположен король. Определить, может ли он одним ходом попасть на поле (с, d);

г) на поле (а, b) расположен ферзь. Определить, угрожает ли он полю (с, d);

д) на поле (а, b) расположена белая пешка. Определить, может ли она одним ходом попасть на поле

(с, d):

— при обычном ходе;
— когда она "бьет" фигуру или пешку соперника.

Белые пешки перемещаются по доске снизу вверх;

е) на поле (а, b) расположена черная пешка. Определить, может ли она одним ходом попасть на поле (c, d):

— при обычном ходе;

— когда она "бьет" фигуру или пешку соперника.

Черные пешки перемещаются по доске сверху вниз;

ж) на поле (а, b) расположен конь. Определить, угрожает ли он полю (с, d).

Во всех задачах ответ проверить на шахматной доске или на клетчатой бумаге.

4.53. Поле шахматной доски определяется парой натуральных чисел, каждое из которых не превосходит восьми: первое число — номер вертикали (при счете слева направо), второе — номер горизонтали (при счете снизу вверх). Даны натуральные числа а, b, с, d, е, f, каждое из которых не превосходит восьми.

На поле (а, b) расположена белая фигура, на поле (с, d) — черная. Определить, может ли белая фигура пойти на поле (е, f), не попав при этом под удар черной фигуры.

Рассмотреть следующие варианты сочетаний белой и черной фигур:

а) ладья и ладья;

б) ладья и ферзь;

в) ладья и конь;

г) ладья и слон;

д) ферзь и ферзь;

е) ферзь и ладья;

ж) ферзь и конь;

з) ферзь и слон;

и) конь и конь;

к) конь и ладья;

л) конь и ферзь;

м) конь и слон;

н) слон и слон;

о) слон и ферзь;

п) слон и конь;

р) слон и ладья;

с) король и слон;

т) король и ферзь;

у) король и конь;

ф) король и ладья.

Во всех задачах ответ проверить на шахматной доске или на клетчатой бумаге.

4.54. Поле шахматной доски определяется парой натуральных чисел, каждое из которых не превосходит восьми: первое число — номер вертикали (при счете слева направо), второе — номер горизонтали (при счете снизу вверх). Даны натуральные числа а, b, с, d, каждое из которых не превосходит восьми. Определить, являются ли поля (а, b) и (c, d) полями одного цвета.

Ответ проверить на шахматной доске или на клетчатой бумаге.

4.55. В подъезде жилого дома имеется n квартир, пронумерованных подряд, начиная с номера а. Определить, является ли сумма номеров всех квартир четным числом. Формулу суммы членов арифметической прогрессии не использовать.

С расчетами

4.56. Дано двузначное число. Определить:

а) входит ли в него цифра 3;

б) входит ли в него цифра А.

4. 57. Дано двузначное число. Определить:

а) входят ли в него цифры 4 или 7;

б) входят ли в него цифры 3, 6 или 9.

4.58. Дано трехзначное число. Определить:

а) входит ли в него цифра 6;

6) входит ли в него цифра N.

4.59. Дано трехзначное число. Определить:

а) входят ли в него цифрв1 4 или 7;

6) входят ли в него цифры 3, 6 или 9.

4.60. Дано четырехзначное число. Определить:

а) входит ли в него цифра 4;

б) входит ли в него цифра В.

4.61. Дано четырехзначное число. Определить:

а) входят ли в него цифры 2 или 7;

6) входят ли в него цифры 3, 6 или 9.

4.62 Дано натуральное число n (n 9999). Выяснить, является ли оно палиндромом ( перевертышем ), с учетом четырех цифр, как, например, числа 7777, 8338, 0330 и т.п. (палиндромом называется число, десятичная запись которого читается одинаково слева направо и справа налево).

4.63. Дано натуральное число n (n < 9999). Выяснить, верно ли, что это число содержит ровно три одинаковые цифры, если оно записано четырьмя цифрами, как, например, числа 3363, 4844, 0300 и т.п.

4.64. Дано натуральное число n (n < 9999). Выяснить, различны ли все четыре цифры этого числа (если оно записано четырьмя цифрами). Например, в числе 3678 все цифры различны, в числе 0023 — нет.

4.65. Определить, является ли заданное шестизначное число счастливым. (Счастливым называют такое шестизначное число, у которого сумма его первых трех цифр равна сумме его последних трех цифр.)

4.66. Имеются стол прямоугольной формы с размерами а х b (а и b — целые числа, а > b) и кости домино с размерами с х d х е (с, d и е — целые числа, с > d > e). Найти вариант размещения на столе наибольшего количества костей. Все размещаемые кости должны лежать на одной и той же грани в один ярус без свешивания со стола. Все ребра костей домино должны быть параллельны или перпендикулярны каждой стороне стола.

4.67. Даны два прямоугольника, стороны которых параллельны или перпендикулярны осям координат. Известны координаты левого нижнего угла каждого из них и длины их сторон. Один из прямоугольников назовем первым, другой — вторым,

а) Определить, принадлежат ли все точки первого прямоугольника второму.

б) Определить, принадлежат ли. все точки одного из прямоугольников другому.

в) Определить, пересекаются ли эти прямоугольники.

Сложных уровня

4.68. Работа светофора для пешеходов запрограммирована следующим образом: в начале каждого часа в течение трех минут горит зеленый сигнал, затем в течение двух минут — красный, в течение трех минут — опять зеленый и т.д. Дано вещественное число t, означающее время в минутах, прошедшее с начала очередного часа. Определить, сигнал какого цвета горит для пешеходов в этот момент.

4.69. Дано целое число k (1 k 365). Определить, каким будет k-й день года: выходным (суббота и воскресенье) или рабочим, если 1 января — понедельник.

4.70. Траектория снаряда, вылетающего из орудия под углом a с начальной скоростью n₀ , задается уравнениями:

х=n₀tcosa;

у= n₀tsina — gt²/2,

где g = 9,8 м/с~ — ускорение свободного падения,

t— время.

Даны значения a и n₀ .Определить, поразит ли снаряд цель высотой Р, расположенную в вертикальной плоскости ствола орудия на расстоянии R на высоте Н.

Неполный

4.71. Дано вещественное число. Вывести на экран его абсолютную величину (условно принимая, что соответствующей стандартной функции нет). Полный условный оператор не использовать.

4.72. Даны два вещественных числа. Условно принимая, что стандартной функции определения абсолютной величины числа нет, найти:

а) полу сумму абсолютных величин заданных чисел;

б) квадратный корень из произведения абсолютных величин заданных чисел.

4.73. Составить программу, которая уменьшает первое введенное число в два раза, если оно больше второго введенного числа по абсолютной величине.

4.74. Даны два числа. Если квадратный корень из второго числа меньше первого числа, то увеличить второе число в пять раз.

4.75. Даны три целых числа. Вывести на экран те из них, которые являются четными.

4.76. Даны три вещественных числа. Возвести в квадрат те из них, значения которых неотрицательны.

4.77. Даны три вещественных числа. Вывести на экран:

а) те из них, которые принадлежат интервалу (1,6 — 3,8);

б) те из них, которые принадлежат интервалу (0,7 — 5,1).

4.78. Даны четыре вещественных числа. Определить, сколько из них отрицательных.

4.79. Даны четыре целых числа. Определить, сколько из них четных.

4.80. Даны четыре вещественных числа. Найти сумму тех чисел, которые больше пяти.

4.81. Даны четыре целых числа. Определить сумму тех из них, которые кратны трем.

4.87. Определить, в какую из областей (I, II или III) попадает точка с заданными координатами (для простоты принять, что абсцисса точки не равна 5 или 1,5):

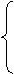4.82. Составить программу для вычисления значения функции у(х):

-1, если x<-1

y= x, если x<1

1, если x=1

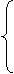4.83. Составить программу для вычисления значения функции z(a):

1, если а>0

z= 0, если а=0

-1, если а<0

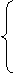4.84 Дано вещественное число x. Вычислить ƒ (x), если:

0, при х≤0,

ƒ = x, при 0<x≤1

x², в остальных случаях

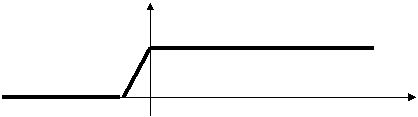
4.85 Дано вещественное число y. Вычислить ƒ (y), если:

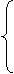2, при y>2

ƒ= 0, при 0<y≤2

-3y, в остальных случаях

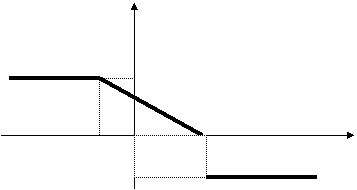
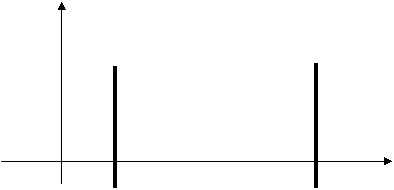
4.86 Для функций, заданных графически, определить значение y при заданном значении x:

y

-1 0 x

y

-1 0 0 x

-1

y

1

-1 0 1 x

4.87 определить, в какую из областей (I, II или III) попадает точка с заданными координатами (для простоты принять, что ордината точки не равна 5 или 1,5):

y

I II III

0 1,5 5 x

4.88. Определить, в какую из областей (I, II или III) попадает точка с заданными координатами (для простоты принять, что ордината точки не равна 5,3 или 2,2):

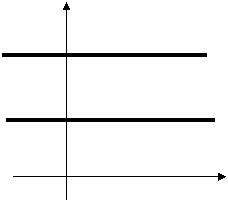
y I

5,3

II

2,2 III

0 x

4.89. В чемпионате по футболу команде за выигрыш дается 3 очка, за проигрыш — 0, за ничью — 1. Известно количество очков, полученных командой за игру. Определить словесный результат игры (выигрыш, проигрыш или ничья).

4.90. Даны вещественные числа а, b, с (а ¹ О). Выяснить, имеет ли уравнение ах²+ bx + с = 0 вещественные корни. Если такие корни имеются, то найти их. В противном случае ответом должно служить сообщение, что вещественных корней нет.

4.91. Даны три различных целых числа. Определить, какое из них (первое, второе или третье):

а) самое большое;

б) самое маленькое;

в) является средним (средним назовем число, которое больше наименьшего из данных чисел, но меньше наибольшего).

4.92. Определить максимальное и минимальное значения из трех различных вещественных чисел.

4.93. Составить программу нахождения суммы двух наибольших из трех различных чисел.

4.94. Составить программу нахождения произведения двух наименьших из трех различных чисел.

4.95. Даны две тройки вещественных чисел. В каждой тройке все числа различные. Найти среднее арифметическое средних чисел каждой тройки (средним назовем такое число в тройке, которое больше наименьшего из чисел данной тройки, но меньше наибольшего).

4.96. Даны три вещественных числа. Используя только два неполных условных оператора, определить:

а) максимальное значение заданных чисел;

б) минимальное значение заданных чисел.

4.97. Вывести на экран номер четверти координатной плоскости, которой принадлежит точка с координатами (х,у), при условии что х ¹ 0 и у ¹ 0.

4.98. Даны вещественные положительные числа а, b, с.Если существует треугольник со сторонами а, b, с, то определить, является ли он прямоугольным.

4.99. Даны вещественные положительные числа а, b, с. Если существует треугольник со сторонами а, b, с, то:

а) определить его вид (прямоугольный, остроугольный или тупоугольный);

б) определить его вид (прямоугольный, остроугольный или тупоугольный) и особенности (равносторонний, равнобедренный, разносторонний).

4.100. Дано целое число n (1 n 99), определяющее возраст человека (в годах). Для этого числа напечатать фразу мне nлет, учитывая при этом, что при некоторых значениях nслово лет надо заменить на слово год или года.

4.101. Для натурального числа k напечатать фразу "мы нашли k грибов в лесу", согласовав окончание слова "гриб" с числом k.

4.102. Дано натуральное число n(1 n 9999), определяющее стоимость товара в копейках. Выразить стоимость в рублях и копейках, например, 3 рубля 21 копейка, 15 рублей 5 копеек, 1 рубль ровно и т.п.

4.103. Дано натуральное число (1 n 1188), определяющее возраст человека (в месяцах). Выразить возраст в годах и месяцах, например, 21 год 10 месяцев, 52 года 1 месяц, 46 лет ровно и т.п.

4.104. Известны год, номер месяца и число дней рождения двух человек (1 — январь и т.п.). Определить возраст каждого человека (число полных лет). Определить, кто из них старше.

4.105. Известны год, номер месяца и день рождения человека, а также год, номер месяца и номер текущего дня месяца (1 — январь и т.п.). Определить возраст человека (число полных лет).

4.106. Известны год и номер месяца рождения человека, а также год и номер месяца сегодняшнего дня (1 — январь и т.п.). Определить возраст человека (число полных лет и число полных месяцев). При определении числа полных месяцев дни месяца не учитывать, а использовать разность между номерами месяцев. Например, если месяц рождения февраль, а текущий (сегодняшний) месяц май, то число полных месяцев равно трем независимо от дней рождения и сегодняшнего.

4.107. Поезд прибывает на станцию в а часов bминут и отправляется в с часов d минут. Пассажир пришел на платформу в nчасов m минут. Будет ли поезд стоять на платформе? Числа а, b, с, d, n, m – целые,0< а 23, 0< b 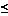59, 0< с 23, 0< d 59, 0 < n 23, 0 < m 59.

4.108 Дата некоторого дня определяется двумя натуральными числами: m (порядковый номер месяца) и n (число). По заданным nи mопределить:

а) дату предыдущего дня (принять, что n и m не определяют 1 января);

б) дату следующего дня (принять, что n и m не определяют 31 декабря).

В обеих задачах принять также, что год не является високосным.

4.109. Дата некоторого дня определяется тремя натуральными числами: g (год), m (порядковый номер месяца) и n(число). По заданным g, n и m определить:

а) дату предыдущего дня;

б) дату следующего дня.

В обеих задачах рассмотреть 2 случая:

а) заданный год не является високосным;

б) заданный год может быть високосным (см. задачу 4.48).

4.110. Работа светофора для водителей запрограммирована следующим образом: в начале каждого часа в течение трех минут горит зеленый сигнал, затем в течение одной минуты — желтый, в течение двух минут— красный, в течение трех минут — опять зеленый и т.д. Дано вещественное число t,означающее время в минутах, прошедшее с начала очередного часа. Определить, сигнал какого цвета горит для водителей в этот момент.

4.111. Дано целое число k (1 k 365). Определить, каким будет k-й день года: субботой, воскресеньем или рабочим днем, если 1 января — понедельник.

4.112. Даны целое число k (1 k 180) и последовательность цифр 10111213...9899, в которой выписаны подряд все двузначные числа. Определить k-ю цифру

При решении данной задачи использовать оператор варианта (выбора). См. также задачу 4.118.

' При решении данной задачи использовать оператор варианта (выбора). См. также задачу 4.125.

4. 113. Дана последовательность цифр, представляющая собой записанные подряд ноль и 20 первых натуральных чисел. Найти цифру с номером и в этой последовательности (1 n 32).

4.114. Даны целое число k (1 k 252) и последовательность цифр 505152...9899100101...149150, в которой выписаны подряд все натуральные числа от 50 до 150. Определить k-ю цифру.

4.115. Даны целое число k (1 k 222) и последовательность цифр 123...91011...9899100101 ...109110, в которой выписаны подряд все натуральные числа от 1 до 110. Определить k-ю цифру

.

3. Оператор варианта (выбора)

4.116. Составить программу, которая в зависимости от порядкового номера дня недели (1, 2, ..., 7) выводит на экран его название (понедельник, вторник, ..., воскресенье).

4.117. Составить программу, которая в зависимости от порядкового номера месяца (1, 2, ..., 12) выводит на экран его название (январь, февраль, ..., декабрь).

4,118. Составить программу, которая в зависимости от порядкового номера месяца (1, 2, ..., 12) выводит на экран количество дней в этом месяце. Рассмотреть 2 случая:

1) год не является високосным (см. задачу 4.48);

2) год високосный (информация об этом вводится с клавиатуры).

4.119. Мастям игральных карт условно присвоены следующие порядковые номера: масти "пики" — 1, масти "трефы" — 2, масти "бубны" — 3, масти "червы" — 4. По заданному номеру масти m (1 m 4) определить название соответствующей масти.

4.120. Игральным картам условно присвоены следующие порядковые номера в зависимости от их достоинства: "валету" — 11, "даме" — 12, "королю" — 13, "тузу" — 14. Порядковые номера остальных карт соответствуют их названиям ( шестерка, девятка и т.п.). По заданному номеру карты k (6 k 14) определить достоинство соответствующей карты.

4.121. Мастям игральных карт условно присвоены следующие порядковые номера: масти "пики" — 1,.масти "трефы" — 2, масти "бубны" — 3, масти "червы"— 4; а достоинству карт: "валету" — 11, "даме" — 12, "королю" — 13, "тузу" — 14 (порядковые номера карт остальных достоинств соответствуют их названиям: шестерка, девятка и т.п.). По заданным номеру масти m (1 m 4) и номеру достоинства карты k (6 k 14) определить полное название (масть
и достоинство) соответствующей карты в виде: дама
пик", "шестерка бубен" — и т.п.

4.122. Дано целое число k (1 k 365). Определить,
каким днем недели (понедельником, вторником,
субботой или воскресеньем) является k-й день не високосного года, в котором 1 января — понедельник.

4.123. С начала 1990 года по некоторый день про-
шло n месяцев и 2 дня (n 1). Определить название
месяца (январь, февраль и т.п.) этого дня.

4.124. Присвоить целочисленной величине х значение 1, 2, ..., 11 или 12 в зависимости от того, каким
месяцем (январем, февралем и т.п.) является месяц
этого дня (см. задачу 4.123). Например, при n = 3
соответствующий месяц — март.

4.125. Дата некоторого дня определяется двумя натуральными числами: m (порядковый номер месяца) и n (число). По заданным m и n определить:

а) дату предыдущего дня (принять, что m и n не определяют 1 января);

б) дату следующего дня (принять, что n и т не определяют 31 декабря).

В обеих задачах принять также, что год не является високосным.

4.126. Дата некоторого дня определяется тремя натуральными числами: g (год), m (порядковый номер месяца) и n(число). По заданным g, n и m определить:

а) дату предыдущего дня;

б) дату следующего дня.

В обеих задачах рассмотреть два случая:

1) заданный год не является високосным;

2) 2) заданный год может быть високосным (см. задачу 4.48).

4.127. В старо японском календаре был принят 60-летний цикл, состоящий из пяти 12-летних подциклов. Под циклы обозначались названиями цветов: зеленый, красный, желтый, белый и черный. Внутри каждого подцикла годы носили названия животных: крыса, корова, тигр, заяц, дракон, змея, лошадь, овца, обезьяна, курица, собака и свинья. Например, 1984 год — год начала очередного цикла — назывался Годом Зеленой Крысы.

Составить программу, которая по заданному номеру года нашей эры nпечатает его название по старо японскому календарю. Рассмотреть два случая:

а) значение n> 1984;

б) значение n может быть любым натуральным
числом.